рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Элементы корреляционного и регрессионного анализа
Реферат Курсовая Конспект
Элементы корреляционного и регрессионного анализа
Элементы корреляционного и регрессионного анализа - раздел Математика, Математической статистике Взаимосвязь Между Различными Параметрами, Признаками, Присущими Живому Органи...
Взаимосвязь между различными параметрами, признаками, присущими живому организму, является объектом пристального внимания врача. Анализ этих взаимосвязей, постоянно меняющихся в процессе жизнедеятельности, – один из основных этапов в клиническом изучении течения заболевания и выздоровления, определении прогноза заболевания.
7.1. Характер взаимосвязи между признаками
Все многообразие связей между отдельными признаками, свойствами явлений или параметрами функционирующего объекта можно разделить на две основные группы: функциональные и статистические.
Зависимость, при которой одному и тому же числовому значению первого признака 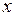 соответствует только одно числовое значение второго признака
соответствует только одно числовое значение второго признака 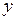 , называется функциональной. Т.е. можно записать, что
, называется функциональной. Т.е. можно записать, что 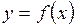 . Примером может служить закон Ома, который устанавливает прямо пропорциональную зависимость между напряжением и током.
. Примером может служить закон Ома, который устанавливает прямо пропорциональную зависимость между напряжением и током.
В живой природе такая однозначная четкая взаимосвязь встречается редко. Чаще проявляется взаимосвязь, при которой одному и тому же числовому значению первого признака соответствует несколько (ряд) случайных значений другого признака. Такая взаимосвязь называется корреляционной (от лат. сorrelatio – соотношение, связь). Простейшим примером может служить наблюдение: при данном росте человек может иметь различный вес.
Существуют несколько видов выражения корреляционной взаимосвязи.
Если признаки выражены количественными (числовыми) характеристиками, то используют коэффициент парной и ранговой корреляции, корреляционное отношение, коэффициент множественной и частной корреляции, коэффициент множественной детерминации.
Связь между признаками, изменения которых носят качественный характер (гиперпигментация кожи, увеличенная и плотная печень и т.п.), изучают, используя коэффициент качественной альтернативной корреляции (тертрахорического показателя), критерия c2, показателя сопряженности Пирсона и Чупрова и др. Имеются методы и для оценки качественно–количественной корреляции (у одного признака изменяется числовое значение, а у другого – качественный показатель. Например, при стенокардии: повышение артериального давления и бледность кожных покровов).
7.2. Проведение корреляционного анализа
с помощью коэффициента парной корреляции
Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию – о взаимосвязи этих параметров.
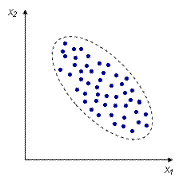
Например, измеряем рост и вес человека или рост и размер обуви. Каждое измерение представлено точкой в двумерном пространстве:

| Рис. 4 |
Несмотря на то, что величины носят случайный характер, в общем, наблюдается некоторая зависимость – величины коррелируют. В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается).
Возможны также такие случаи ( рис.5-7):
Отрицательная корреляция:
| Отсутствие корреляции:

| Нелинейная корреляция:

|
| Рис.5 | Рис.6 | Рис.7 |
Взаимосвязь между переменными необходимо охарактеризовать численно, чтобы, например, различать случаи, приведенные на рис.8 и рис.9.

| 
|
Рис. 8 Рис. 9
Все, что мы видим на приведенных выше рисунках, называют диаграммой рассеивания.
Если облако точек напоминает очертания некоторой линии, то можно предполагать, что мы видим на диаграмме рассеяния именно такую по форме зависимость, однако искаженную воздействием как случайных, так и неучтенных факторов, вызывающим отклонение точек от теоретической формы.
Поскольку наиболее простой формой в математике является прямая пропорциональная зависимость, то в корреляционном и регрессионном анализе наиболее популярны линейные модели.
Для численных оценок вводится коэффициент корреляции (коэффициент парной корреляции)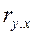 .
.
Для линейной связи переменных он рассчитывается по формуле Пирсона:
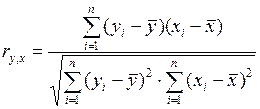 .
.
Коэффициент корреляции 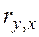 изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между
изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между 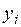 и xi. Коэффициент корреляции равен 1 (или -1), если связь линейна.
и xi. Коэффициент корреляции равен 1 (или -1), если связь линейна.
Коэффициент парной корреляции вычисляется для количественных признаков. Коэффициент корреляции симметричен, т.е. не изменяется, если X и Y поменять местами, и является величиной безразмерной.
Коэффициент корреляции не изменяется при изменении единиц измерения признаков X и Y.
Сам по себе коэффициент корреляции не имеет содержательной интерпретации. Однако его квадрат (r2), называемый коэффициентом детерминации (обозначается d и обычно выражается в %), имеет простой смысл – это показатель того, насколько изменения зависимого признака объясняются изменениями независимого.
Более точно, это доля дисперсии (разброса) одного признака, объясняемая влиянием другого (если связь интерпретировать как причинно-следственную).
Из определения коэффициента детерминации следует, что он принимает значения в диапазоне от 0 до 100%.
Если две переменные функционально линейно зависимы (точки на диаграмме рассеяния лежат на одной прямой), то можно сказать, что изменение одной из них полностью объясняется изменением другой. Это как раз тот случай, когда коэффициент детерминации равен 100% (при этом коэффициент корреляции может быть равен как 1, так и –1).
Коэффициенты корреляции и детерминации
Если две переменные линейно независимы (метод наименьших квадратов, о котором пойдет речь в следующем параграфе, дает горизонтальную прямую), то одна из них в своих изменениях никоим образом не определяет другую – в этом случае коэффициент детерминации равен нулю. В остальных случаях коэффициент детерминации указывает, какая часть изменений одной переменной объясняется изменениями другой переменной.
Чем выше по модулю (по абсолютной величине) значение коэффициента корреляции, тем сильнее связь между признаками.
Принято считать, что коэффициенты корреляции, которые по модулю больше 0,7, свидетельствуют о сильной связи (при этом коэффициенты детерминации > 50%, т.е. один признак определяет другой более чем наполовину). Коэффициенты корреляции, которые по модулю меньше 0,7, но больше 0,5, говорят о связи средней силы (при этом коэффициенты детерминации меньше 50%, но больше 25%). Наконец, коэффициенты корреляции, которые по модулю меньше 0,5, говорят о слабой связи (при этом коэффициенты детерминации меньше 25%).
Оценить глубину и характер корреляционной связи можно, пользуясь табл. 2:
Таблица 2
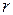
| Глубина связи |
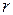 =0 =0
| Отсутствует |

| Слабая |

| Умеренная |

| Значительная |

| Сильная |
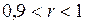
| Очень сильная |
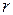 =1 =1
| Полная |
Если  >0, то связь прямая (положительная), при
>0, то связь прямая (положительная), при  <0 связь обратная (отрицательная).
<0 связь обратная (отрицательная).
Методами корреляционного анализа решаются задачи:
1. Взаимосвязь. Есть ли взаимосвязь между параметрами?
2. Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.
3. Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.
7.3. Элементы регрессионного анализа
После того, как установлено наличие корреляционной связи между двумя изучаемыми признаками (явлениями), можно попытаться установить закономерность зависимости одного признака 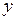 , являющегося в нашем случае функцией, от другого
, являющегося в нашем случае функцией, от другого 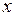 (аргумента). Зная закономерность
(аргумента). Зная закономерность 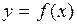 , можно в дальнейшем прогнозировать течение процесса, обладающего признаками
, можно в дальнейшем прогнозировать течение процесса, обладающего признаками 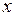 и
и 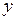 , изучать его динамику.
, изучать его динамику.
Чтобы получить уравнение 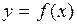 , требуется аппроксимировать (лат. approximare – приближаться) эмпирическую линию регрессии (ЭЛР), которую получают путем соединения точек диаграммы (рис. 10) подходящей теоретической линией регрессии (ТЛР).
, требуется аппроксимировать (лат. approximare – приближаться) эмпирическую линию регрессии (ЭЛР), которую получают путем соединения точек диаграммы (рис. 10) подходящей теоретической линией регрессии (ТЛР).
На рис.10 показана нелинейная (а) и линейная (б) связь между величинами.
 |
а)
 |
б)
Рис. 10
Выше мы говорили о простейшей корреляционной связи – линейной. Поэтому все внимание обратим на рис. 10,б. Для этого случая уравнение связи 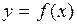 следует искать в виде теоретического уравнения прямой:
следует искать в виде теоретического уравнения прямой:
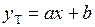 .
.
Для того чтобы получить конкретное уравнение связи, необходимо определить коэффициенты a и b. Определение коэффициентов уравнения ТЛР производится различными способами, самым точным из них является метод наименьших квадратов. Название метода происходит из основного требования замены ЭЛР на ТЛР – аппроксимация будет осуществлена наилучшим образом, если ТЛР наилучшим образом будет приближаться к ЭЛР, в этом случае сумма отклонений значений функции из уравнения ТЛР – yТ от значений функции в эксперименте – yЭ (для одного и того же значения аргумента x) будет минимальной:
 .
.
Для устранения влияния знака разности берут квадраты:
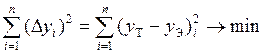 ,
,
но 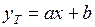 , тогда можно записать:
, тогда можно записать:
 .
.
Известно, что если функция в некоторой точке имеет минимум, то производная ее в этой точке равна 0. Поэтому приравниваем нулю производные суммы по параметрам a и b. Полученную систему уравнений решаем относительно a и b. Полученные значения коэффициентов подставляем в уравнение 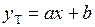 и получаем уравнение теоретической линии регрессии, наилучшим образом описывающее закон связи коррелирующих признаков x и y.
и получаем уравнение теоретической линии регрессии, наилучшим образом описывающее закон связи коррелирующих признаков x и y.
Поиск аппроксимирующего уравнения – это искусство, которым можно овладеть только в результате накопления большого опыта. На помощь экспериментаторам в настоящее время пришли многочисленные программы для обработки экспериментальных данных. В частности, кривую ТЛР на рис. 10,а можно описать при помощи уравнения

Конечно, без помощи вычислительной машины и соответствующих программ найти все коэффициенты в этом уравнении довольно трудно. Но вряд ли даже исследователь будет пользоваться этим уравнением: слишком много параметров. Оказывается, можно подобрать несколько кривых ТЛР ( теоретической линии регрессии). При обработке экспериментальных данных исследователю помогает еще здравый смысл, представление о возможном характере взаимосвязи величин. Все это позволяет выбрать наиболее подходящее уравнение для описания полученных экспериментальных закономерностей.
Чаще при обработке эксперимента на начальном этапе исследователь ограничивается графическим проведением ТЛР с учетом метода наименьших квадратов: кривая должна быть плавной и равноотстоять от всех экспериментальных точек.
– Конец работы –
Эта тема принадлежит разделу:
Математической статистике
высшего профессионального образования... Пермская государственная медицинская академия... имени академика Е А Вагнера...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Элементы корреляционного и регрессионного анализа
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов