Аналитическая геометрия на плоскости

Установление связи между алгеброй и геометрией было, по существу, революцией в математике. Это позволило воспринимать математику как единую науку и способствовало ее быстрому развитию. Создателем метода координат считают Рене Декарта, который дал описание метода координат и его применения к решению геометрических задач. Развитие идей Декарта привело к развитию целой ветви математики, которая решает геометрические задачи аналитически, т.е. алгебраическими методами и методами анализа. Эту часть математики называют аналитической геометрией.

1) Прямоугольная система координат – две взаимно перпендикулярные прямые (горизонтальная и вертикальная) с заданным масштабом.

2) Полярная система координат

Пусть на плоскости даны некоторая точка О и проходящая через нее ось ОХ. Положение любой точки М плоскости определяется расстоянием этой точки от полюса – радиус-вектором r и полярным углом 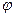между полярной осью и радиус-вектором.

Две координаты (r, 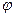) определяют единственную точку плоскости и называются ее полярными координатами ().

Можно установить связь между декартовыми и полярными координатами одной и той же точки.

Обозначим через декартовы координаты точки М, через ее полярные координаты. Тогда зависимость между полярными координатами (r, 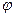) точки М и ее прямоугольными координатами выражается формулами:

и обратно

.

Пример 1. Даны декартовы координаты точки М(1,-1). Найти ее полярные координаты.

Решение.

Так как х=1>0 и у=-1<0, то точка М находится в IV четверти, а значит

Итак, полярные координаты точки М().

Пример 2. Преобразовать к полярным координатам уравнение линии .

Решение.

;

;

 

 

Прямая линия и ее уравнения

В аналитической геометрии всякую линию рассматривают как геометрическое место точек, удовлетворяющих определенному свойству.

Линии на плоскости соответствует некоторое уравнение с двумя переменными х и у, , которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащие на ней. Такое уравнение называется уравнением данной линии.

1. Уравнение прямой с угловым коэффициентом

Всякая прямая в декартовой система координат может быть представлена уравнением первой степени и, наоборот, всякое уравнение первой степени относительно х и у определяет прямую линию.

Рассмотрим прямую, не параллельную осям координат. Положение ее на плоскости вполне определяется заданием угла наклона прямой к оси ОХ и ординатой точки В, точки пересечения прямой с осью OY (обозначим через 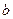). Угол наклона прямой к оси ОХ обозначим через , .

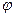Тогда уравнение прямой будет иметь вид

.

Пусть заданы две прямые

,

.

Формула для вычисления угла между двумя прямыми имеет вид:

Исходя из данной формулы, определим условия параллельности и перпендикулярности двух прямых:

а) две прямые параллельны тогда и только тогда, когда ;

б) две прямые перпендикулярны тогда и только тогда, когда .

2. Общее уравнение прямой имеет вид

,

где А и В – произвольные числа, не равные нулю одновременно.

3. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом

Найдем уравнение прямой с данным угловым коэффициентом , проходящей через данную точку М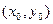. Тогда уравнение прямой будет иметь вид:

.

4. Уравнение прямой, проходящей через две данные точки

Даны две точки и . Тогда уравнение прямой, проходящей через эти точки имеет вид:

.

5. Уравнение прямой в отрезках

Пусть даны точки и , . Уравнение прямой, проходящей через эти точки имеет вид:

6. Уравнение прямой с нормальным вектором , проходящей через точку имеет вид:

Нормальный вектор – это вектор, перпендикулярный данной прямой.

7. Каноническое уравнение прямой по точке и направляющему вектору имеет вид:

.

Направляющий вектор – вектор, параллельный данной прямой.

8. Параметрические уравнения прямой

.

Пример. Треугольник АВС задан своими вершинами А(1; 3), В(-2; 0), С(4; -1). Составить уравнение средней линии треугольника АВС, параллельной прямой ВС, и высоты, опущенной из вершины А.

Решение. а) Найдем середины отрезков АВ и АС (точки М и N соответственно):

; .

Составим уравнение прямой MN по двум точкам:

;

;

- уравнение средней линии треугольника АВС, параллельной ВС.

б) Из вершины А треугольника АВС опустим перпендикуляр АН, и составим уравнение этой прямой.

Прежде всего составим уравнение прямой ВС:

;

; ; .

Так как .

Тогда, уравнение прямой АН с угловым коэффициентом и проходящей через точку А(1;3) имеет вид:

;

;

- уравнение высоты треугольника АВС, опущенной из вершины А.

 

Расстояние от точки до прямой

Для вычисления расстояния от точки до прямой используется формула

 

Кривые второго порядка

Общее уравнение второго порядка относительно х и у члены второй степени (), первой степени () и нулевой степени (свободный член), имеет вид:

.

Хотя бы один из коэффициентов А, В, С должен быть отличен от нуля.

Данной уравнение является уравнением второй степени, а линии, уравнения которых описываются этими уравнениями, называются кривыми второго порядка на плоскости.

1. Окружность

Окружность – геометрическое место точек, равноудаленных от точки на расстояние R.

Точка С называется центром окружности, R – радиус данной окружности.

Уравнение окружности с центром в точке и с радиусом R имеет вид:

.

Замечание 1. Если начало координат совпадает с центром окружности, то ее уравнение имеет вид:

.

Такое уравнение называется каноническим уравнением окружности.

Пример. Привести к каноническому виду уравнение второго порядка

.

Решение. Сгруппируем члены, содержащие х, и отдельно члены, содержащие у, и выделим их полные квадраты.

;

;

;

;

.

Мы получили уравнение окружности с центром в точке С(1, -2) и радиусом, равным 3.

2. Эллипс

Эллипс – это геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Каноническое уравнение эллипса в выбранной системе координат имеет вид:

,

где .

Вершины эллипса имеют следующие координаты:

.

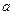Отрезок - большая ось эллипса, отрезок - малая ось эллипса, соответственно и 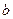- большая и малая полуоси эллипса.

Фокуса эллипса имеют следующие координаты:

. Ось симметрии эллипса, на которой находятся фокусы, называется фокальной осью.

Замечание 1. Если , тогда каноническое уравнение эллипса примет вид и определяет окружность, а значит, окружность можно рассматривать как частный случай эллипса с равными полуосями.

Замечание 2. Число называется эксцентриситетом эллипса.

Для эллипса (для окружности ). Величина эксцентриситета влияет на форму эллипса. Так, при очень малом 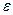полуос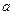и и 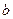почти равны и эллипс напоминает окружность. Если же величина 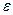близка к единице, то эллипс имеет сильно вытянутую форму.

Замечание 3. Если фокусы эллипса расположены на оси OY, то эллипс «вытягивается» вдоль оси OY, тогда фокусы имеют координаты , .

Пример. Составить каноническое уравнение эллипса, зная, что расстояние между фокусами равно 8, а малая полуось .

Решение. По условию, .

Мы знаем, что .

Итак, каноническое уравнение эллипса имеет вид

.

3. Гипербола

Гиперболой называется геометрическое место точек на плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная.

Каноническое уравнение гиперболы в выбранной системе координат имеет вид:

,

где .

Вершины эллипса имеют следующие координаты:

.

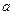Отрезок - большая ось эллипса, отрезок - малая ось эллипса, соответственно и 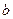- большая и малая полуоси эллипса.

Фокуса эллипса имеют следующие координаты:

.

Асимптоты гиперболы – это прямые и .

При гипербола называется равносторонней.

Замечание 1. Если мнимая ось гиперболы равна и расположена на оси ОХ, а действительная ось равна и расположена на оси ОY, то уравнение такой гиперболы имеет вид:

.

Замечание 2. Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной оси:

.

Для любой гиперболы , это число определяет форму гиперболы.

4. Парабола

Парабола есть геометрическое место точек на плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Каноническое уравнений параболы в выбранной системе координат имеет вид:

.

Уравнение директрисы имеет вид:

.

Фокус имеет координаты .

Замечание 1. Уравнение определяет параболу, область определения которой х<0.

Замечание 2. Парабола имеет вершину в начале координат, фокус , директрису , ветви параболы направлены в положительную сторону оси ОY, и ветви направлены в отрицательную сторону оси OY, если уравнение параболы .