рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вихідні дані до задач
Реферат Курсовая Конспект
Вихідні дані до задач
Вихідні дані до задач - раздел Математика, Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика Варіант Задача ...
| Варіант | Задача | ||||||||||||
| N | n | m | k | P1 | P2 | P1 | P2 | P3 | P4 | P | n | k | |
| 0.75 | 0.85 | 0.6 | 0.4 | 0.95 | 0.98 | 0.1 | |||||||
| 0.55 | 0.45 | 0.55 | 0.45 | 0.8 | 0.7 | 0.2 | |||||||
| 0.6 | 0.7 | 0.65 | 0.35 | 0.96 | 0.9 | 0.25 | |||||||
| 0.85 | 0.65 | 0.75 | 0.25 | 0.75 | 0.7 | 0.3 | |||||||
| 0.65 | 0.95 | 0.56 | 0.44 | 0.85 | 0.8 | 0.2 | |||||||
| 0.9 | 0.8 | 0.7 | 0.3 | 0.8 | 0.9 | 0.3 | |||||||
| 0.7 | 0.75 | 0.52 | 0.48 | 0.85 | 0.7 | 0.5 | |||||||
| 0.75 | 0.8 | 0.35 | 0.65 | 0.8 | 0.95 | 0.3 | |||||||
| 0.85 | 0.95 | 0.33 | 0.67 | 0.55 | 0.6 | 0.1 | |||||||
| 0.75 | 0.9 | 0.34 | 0.66 | 0.65 | 0.7 | 0.2 | |||||||
| 0.45 | 0.65 | 0.51 | 0.49 | 0.85 | 0.75 | 0.4 | |||||||
| 0.95 | 0.9 | 0.54 | 0.46 | 0.95 | 0.85 | 0.3 | |||||||
| 0.6 | 0.5 | 0.47 | 0.53 | 0.92 | 0.83 | 0.25 | |||||||
| 0.65 | 0.75 | 0.39 | 0.61 | 0.75 | 0.77 | 0.15 | |||||||
| 0.75 | 0.95 | 0.38 | 0.62 | 0.94 | 0.8 | 0.1 | |||||||
| 0.55 | 0.6 | 0.37 | 0.63 | 0.92 | 0.9 | 0.2 | |||||||
| 0.65 | 0.7 | 0.47 | 0.53 | 0.82 | 0.8 | 0.3 | |||||||
| 0.65 | 0.6 | 0.7 | 0.3 | 0.85 | 0.78 | 0.35 | |||||||
| 0.85 | 0.8 | 0.71 | 0.29 | 0.59 | 0.65 | 0.4 | |||||||
| 0.35 | 0.45 | 0.72 | 0.28 | 0.67 | 0.7 | 0.45 | |||||||
| 0.55 | 0.65 | 0.73 | 0.27 | 0.55 | 0.7 | 0.25 | |||||||
| 0.8 | 0.6 | 0.74 | 0.26 | 0.65 | 0.75 | 0.1 | |||||||
| 0.7 | 0.55 | 0.75 | 0.25 | 0.75 | 0.9 | 0.15 | |||||||
| 0.9 | 0.75 | 0.76 | 0.24 | 0.84 | 0.8 | 0.2 | |||||||
| 0.8 | 0.65 | 0.77 | 0.23 | 0.9 | 0.95 | 0.4 |
| Варіант | Задача | ||||||||||
| P | n | a | a | s | X1 | X2 | d | n | 
| d | |
Розв’язування типових прикладів
Завдання 1.
Ящик з N однаковими виробами містить n бракованих. Випадково відібрані m виробів і відправлені в магазин. Знайти ймовірність того, що серед них рівно k бракованих.
Розв’язок.
Загальне число можливих елементарних випадків дорівнює числу способів, яки можна вибрати m виробів з N, тобто дорівнює C - числу комбінацій з N елементів по m.
- числу комбінацій з N елементів по m.
Число випадків,що сприяють появі події: серед m виробів рівно k бракованих; причому k бракованих виробів можна вибрати з n бракованих виробів С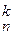 способами; при цьому інші m – k виробів повинні бути не бракованими, котрі вибираються з загальної кількості N – n не бракованих виробів
способами; при цьому інші m – k виробів повинні бути не бракованими, котрі вибираються з загальної кількості N – n не бракованих виробів 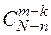 способами. Отже, число сприятливих випадків дорівнює С
способами. Отже, число сприятливих випадків дорівнює С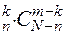 .
.
Шукана ймовірність дорівнює відношенню числа випадків, сприятливих появі події, до числа всіх елементарних випадків:
Р = 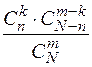 .
.
Наприклад, при N = 100; n = 10; m = 5; k = 3 P = 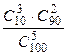
Завдання 2.
Ймовірності влучення в ціль при стрілянині з двох гармат такі: Р1 = 0.8; Р2=0,9. З обох гармат зробили по одному залпу. Знайти ймовірності: а) двох улучень; б) жодного влучення; в) тільки одного влучення; г) хоча б одного влучення.
Розв’язок.
Позначимо події:
А - улучення з першої гармати ;
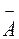 - невлучення з першої гармати;
- невлучення з першої гармати;
В - улучення з другої гармати;
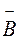 - невлучення з другої гармати.
- невлучення з другої гармати.
Тоді  =
= 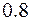 ;
; 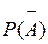 =
= 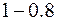 =
= 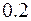 ;
; 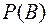 =
= 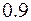 ;
;  =
=  =
=  .
.
а) Подія АВ позначає, що мало місце влучення з обох гармат. У свою чергу, події А и В незалежні, отже,
Р(АВ) = Р(А) × Р(В) = 0.8 × 0.9 = 0.72.
б) Подія 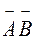 позначає, що мав місце промах (невлучення) з обох
позначає, що мав місце промах (невлучення) з обох
гармат. Тому що події 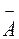 і
і 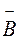 незалежні,
незалежні,
 =
=  = 0.2 × 0.1 = 0.02.
= 0.2 × 0.1 = 0.02.
в) Подія 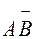 +
+ 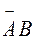 полягає в тому, що мало місце тільки одне влучення: чи влучення з першої гармати , а з другої промах, чи влучення з другої гармати , а з першої промах. Події
полягає в тому, що мало місце тільки одне влучення: чи влучення з першої гармати , а з другої промах, чи влучення з другої гармати , а з першої промах. Події  і
і 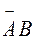 несумісні, тому
несумісні, тому
 +
+ 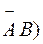 =
= 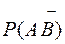 +
+ 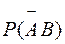 .
.
Події  і
і 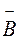 , а також
, а також 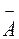 і
і 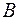 незалежні, отже,
незалежні, отже,
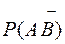 =
= 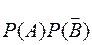 = 0.8 × 0.1 = 0.08;
= 0.8 × 0.1 = 0.08;
 =
= 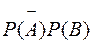 = 0.2 × 0.9 = 0.18;
= 0.2 × 0.9 = 0.18;
 +
+ 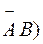 = 0.08 + 0.18 = 0.26.
= 0.08 + 0.18 = 0.26.
г) Нехай Р – ймовірність того, що має місце хоча б одне влучення. Тоді, враховуючи незалежність подій 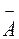 і
і 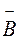 , знайдемо
, знайдемо
Р =  -
- 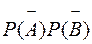 = 1- 0.2 × 0.1 = 0.98.
= 1- 0.2 × 0.1 = 0.98.
Завдання 3.
Виріб перевіряється на стандартність одним із двох товарознавців. Ймовірність того, що виріб потрапить до першого товарознавця, дорівнює 0.55, а до другого – 0.45. Ймовірність того, що виріб буде визнано стандартним першим товарознавцем, дорівнює 0.9, а другим – 0.98.
Знайти ймовірність того, що: а) виріб, що надійшов на перевірку, буде визнано стандартним; б)виріб перевірив другий товарознавець, якщо воно було визнано стандартним
Розв’язок.
Позначимо події:
А – виріб при перевірці визнано стандартним;
В1 – виріб перевірив перший товарознавець;
В2 – виріб перевірив другий товарознавець.
Події В1 і В2 несумісні і утворюють повну групу.
а) Очевидно, що Р(А/В1) = 0.9 – ймовірність того, що виріб визнаний стандартним першим товарознавцем, а Р(А/В2) = 0.98 – ймовірність того, що виріб визнаний стандартним другим товарознавцем. Згідно з формулою повної ймовірності маємо:
Р(А) = Р(А/В1) × Р(В1) + Р(А/В2 )× Р(В2) = 0.9 × 0.55 + 0.98 × 0.495 + 0.441 = 0.936.
б) За умовою задачі необхідно знайти Р(В2/А). Згідно з формулою Бейєса
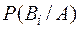 =
= 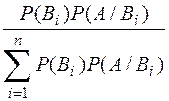 ,
,
маємо:
Р(В2/А)= 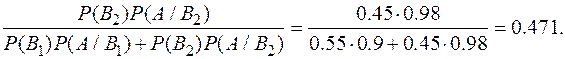
Завдання 4.
Ймовірність того, що навмання узятий виріб нестандартний, дорівнює 0.1. Знайти ймовірність того, що серед узятих п'яти виробів виявиться: а) два нестандартних, б) не більш двох нестандартних.
Розв’язок.
За умовою n = 5; k = 2; p = 0.1; q = 1 – 0.1 = 0.9.
а) Скористаємося формулою Бернуллі
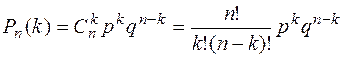
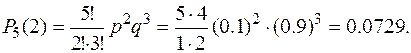
б) Подія А – не більш двох нестандартних виробів, є сума трьох несумісних подій: жодного нестандартного, одне стандартне і два нестандартних.

Завдання 5.
При виготовленні виробів брак складає 5%. Скласти закон розподілу числа бракованих виробів з 6-ти узятих навмання. Знайти М(Х), D(
Розв’язок.
Випадкова величина Х – число бракованих виробів – може приймати значення: 0, 1, 2, 3, 4, 5, 6. Відповідні ймовірності обчислимо за формулою Бернуллі
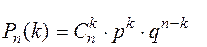
За умовою задачі n = 5; p = 0.05; q = 0.95.
Маємо:
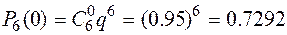 ;
;
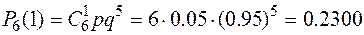 ;
;
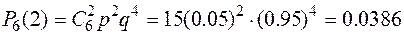 ;
;
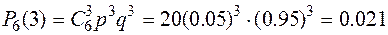 ;
;
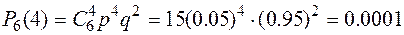 ;
;
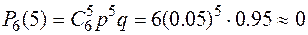 ;
;
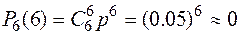 .
.
Отриманий закон розподілу є біномним і має вид
| х | |||||||
| р | 0.7292 | 0.2300 | 0.0386 | 0.0021 | 0.0001 |
Легко перевірити, що 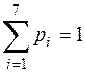
Математичне сподівання біномного розподілу дорівнює
M(X) = np, а дисперсія дорівнює D(Х) = npq. Отже, маємо:
М(Х) = 6 × 0.05 = 0.3;
D(Х) = 6 × 0.05 × 0.95 = 0.285.
Завдання 6.
Дано інтегральну функцію розподілу випадкової величини Х
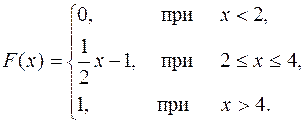
Знайти щільність розподілу 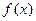 , М(Х), D(Х). Побудувати графіки F(x) і
, М(Х), D(Х). Побудувати графіки F(x) і 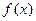 .
.
Розв’язок.
Графік інтегральної функції F(x)

 |

Диференціальна функція (щільність розподілу):

Її графік
 |
 .
.
 .
.
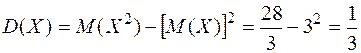 .
.
Завдання 7.
Вага окремого яблука даної партії є випадкова величина Х, розподілена за нормальним законом з математичним сподіванням а = =140г і середнім квадратичним відхиленням  . Визначити ймовірність того, що вага обраного випадковим образом з даної партії яблука: а) знаходиться від 124г до 148г; б) відхиляється від середньої ваги а = 140г не більш, ніж на
. Визначити ймовірність того, що вага обраного випадковим образом з даної партії яблука: а) знаходиться від 124г до 148г; б) відхиляється від середньої ваги а = 140г не більш, ніж на 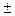 8г.
8г.
Розв’язок.
Маємо: 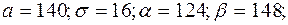
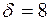
а) Ймовірність того, що вага обраного яблука знаходиться в інтервалі (124; 148) знайдемо по формулі
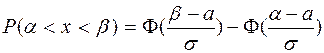
отже, 
Значення функції Ф(х) знаходимо по таблиці значень функції Лапласа, причому, з огляду на непарність функції Ф(-х) = -Ф(х).
б) Ймовірність того, що вага обраного яблука відхиляється від а не більш, ніж на d, знайдемо за формулою:
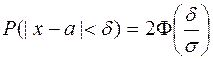 .
.
Маємо: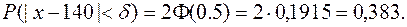
Завдання 8.
При проведенні контрольних іспитів 25 духових шаф були визначені оцінки математичного сподівання і середнього квадратичного відхилення їхнього терміну служби і виявилися рівними  год. і
год. і 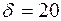 год. Вважаючи, що термін служби кожної духової шафи є нормально розподіленою випадковою величиною, визначити надійний інтервал для оцінки невідомого математичного чекання а при довірливій ймовірності (надійності)
год. Вважаючи, що термін служби кожної духової шафи є нормально розподіленою випадковою величиною, визначити надійний інтервал для оцінки невідомого математичного чекання а при довірливій ймовірності (надійності) 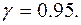
Розв’язок.
Якщо заздалегідь відома величина середнього квадратичного відхилення 
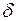 , то границі надійного інтервалу для оцінки математичного сподівання мають вид
, то границі надійного інтервалу для оцінки математичного сподівання мають вид
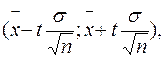
де  - середнє вибіркове;
- середнє вибіркове;
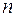 - об’єм вибірки;
- об’єм вибірки;
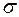 - відоме середнє квадратичне відхилення генеральної сукупності;
- відоме середнє квадратичне відхилення генеральної сукупності;
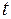 - величина, що визначається за таблицею значень функції Лапласа
- величина, що визначається за таблицею значень функції Лапласа
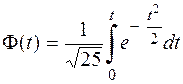 зі співвідношення
зі співвідношення 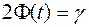 , де
, де 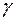 - заздалегідь обрана довірлива ймовірність.
- заздалегідь обрана довірлива ймовірність.
Тому що 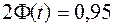 , то
, то 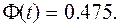 По таблиці значень функції Лапласа знаходимо
По таблиці значень функції Лапласа знаходимо 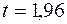 , тоді точність оцінки
, тоді точність оцінки
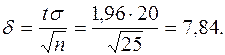
Нижня границя надійного інтервалу 3000 – 7.84 = 2992.16; а верхня границя 3000 + 7.84 = 3007.84. Таким чином, значення невідомого параметра а, що узгоджуються з даними вибірки, задовольняють нерівності
2992,12 < а < 3007,84.
Варто розуміти, що довірлива ймовірність пов'язана тут не з величиною параметра а, а лише з границями інтервалу, що, очевидно, змінюються при зміні вибірки. Надійність  указує на те, що якщо зроблене досить велике число вибірок, то 95% з них визначає такі надійні інтервали, які дійсно містять математичне сподівання і лише в 5% випадків воно може вийти за границі надійного інтервалу.
указує на те, що якщо зроблене досить велике число вибірок, то 95% з них визначає такі надійні інтервали, які дійсно містять математичне сподівання і лише в 5% випадків воно може вийти за границі надійного інтервалу.
Завдання 9.
За даними вибіркового обстеження п’яти крамниць залежність затрат на маркетинг Х (тис. грн.) і обсягом реалізації Y (млн. грн.) має вигляд
 1 3 4 5 7
1 3 4 5 7
 55 85 100 145 115
55 85 100 145 115
Припускаючи, що між Х і Y має місце лінійний кореляційний зв’язок, визначити вибіркове рівняння лінійної регресії.
► Вихідні дані і проміжні розрахунки заносимо в таблицю
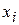
| 
| 
| 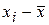
| 
| 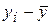
| 
|
| -3 | -45 | |||||
| -1 | -15 | |||||

| 
| 
| 
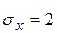
| 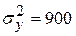
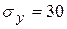
|
Отже, маємо
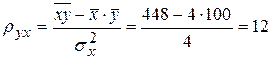 .
.
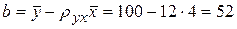 .
.
Отже, шукане рівняння регресії має вигляд
 .
.
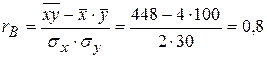 .
.
Розрахунки підтвердили, що між товарообігом і чисельністю робітників обмеженої групи крамниць спостерігається додатний лінійний кореляційний зв’язок, який відповідно таблиці Чеддока можна вважати високим 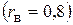 . ◄
. ◄
– Конец работы –
Эта тема принадлежит разделу:
Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика
ХАРКІВСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ ХАРЧУВАННЯ... ТА ТОРГІВЛІ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Вихідні дані до задач
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов