рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Реферат Курсовая Конспект
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ - раздел Математика, Министерство Образования Республики Беларусь...
Министерство образования Республики Беларусь
Учреждение образования
Гомельский государственный университет
имени Франциска Скорины»
А. Р. МИРОТИН, Ж. Н. КУЛЬБАКОВА
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Лабораторный практикум
Для студентов математического факультета
Специальности 1-31 03 01 Математика
Гомель 2009
УДК 517 (075.08)
ББК 22.11 я 73
М 644
Рецензенты:
Ю. В. Малинковский, профессор, доктор физико-математических наук;
В. Н. Семенчук, профессор, доктор физико-математических наук.
Рекомендовано к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины»
Миротин, А. Р.
для студентов математического факультета специальности 1-31 03 01 Математика / А. Р. Миротин, Ж. Н. Кульбакова; М-во образования РБ, Гомельский…Введение
Учебная программа курса «Функциональный анализ и интегральные уравнения» предполагает в качестве формы контроля знаний выполнение лабораторных работ. Целью этих работ является закрепление теоретического материала путем самостоятельного решения задач. Настоящее пособие призвано оказать помощь студентам в овладении основными приемами и методами решения задач по функциональному анализу. Оно содержит задания лабораторных работ 5 семестра, взятые из пособия [3], а также примеры решения типовых задач. При этом важно отметить следующее:
– каждая лабораторная работа рассчитана на 4 – 6 часов аудиторных занятий (в зависимости от ее объема). На первом занятии обсуждаются узловые вопросы темы, а второе (и третье) отводятся для завершения работы и защиты отчета;
– задание каждой лабораторной работы, как правило, выполняется группой из 2 – 3 человек;
– лабораторная работа засчитывается, если должное владение материалом продемонстрировали все члены группы;
– количество защищенных лабораторных работ учитывается на экзамене в рамках рейтинговой накопительной системы оценки знаний студента.
Отчет по лабораторной работе должен быть оформлен в соответствии со следующими требованиями:
– он выполняется письменно каждым членом группы в специальной тетради;
– решение каждой задачи должно быть подробно обосновано и содержать ссылки на все используемые определения и теоремы.
Лабораторная работа 1
Метрические пространства. Сходящиеся
 последовательности в метрических пространствах
последовательности в метрических пространствах
Примеры решения задач
Задача 1 Проверить, сходится ли заданная последовательность xn точек метрического
пространства X к точке a.
Пример 1 xn = 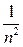
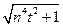 , a = |t| , X = C[-4;4].
, a = |t| , X = C[-4;4].
Решение. Рассмотрим расстояние ρC(xn , a)=  | xn(t) – a(t) |. Так как при всех
| xn(t) – a(t) |. Так как при всех 
|xn(t) – a(t)| = | 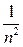
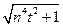 – |t|| =
– |t|| = 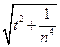 – |t| =
– |t| =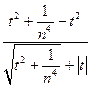

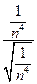 =
= 

 0
0
при n
 , то ρC(xn,a)
, то ρC(xn,a) . Значит, xn сходится к a в C[-4;4].
. Значит, xn сходится к a в C[-4;4].
Пример 2 xn(t) = t n - t n+1 + t, a(t) = t, X = C[0;1].
Решение. Рассмотрим ρC(xn , a) =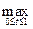 |t n - t n+1|. Обозначим tn - tn+1 через Δn(t) и найдем наибольшее значение функции |Δn(t)| = Δn(t) = tn - tn+1 на отрезке
|t n - t n+1|. Обозначим tn - tn+1 через Δn(t) и найдем наибольшее значение функции |Δn(t)| = Δn(t) = tn - tn+1 на отрезке  . Имеем
. Имеем  = nt n-1 - (n+1)t n ,
= nt n-1 - (n+1)t n ,  =0, если t = 0 или t =
=0, если t = 0 или t =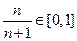 ,
,

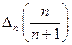 =
=  =
=  =
=  .
.
Δn(0) = 0, Δn(1) =0.
Значит (по правилу нахождения наибольшего значения функции на отрезке),
ρC(xn,a) = 

 0 = 0,
0 = 0,
а потому xn сходится к a в C[0;1].
Пример 3 xn = , a = (0,0,0,…), X = l3.
, a = (0,0,0,…), X = l3.
Решение.
ρ3(xn , a) =  при n
при n 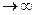 .
.
Так как ρ3(xn , a) не стремится к нулю, то xn не сходится к a в l3.
Пример 4 xn = , a = (0,0,0,…), X = l2.
, a = (0,0,0,…), X = l2.
Решение.
ρ2(xn , a) = 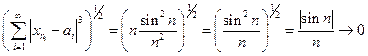 при n
при n 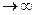 .
.
Значит, xn сходится к a в l2.
Пример 5xn= n , a =
, a = 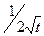 , X=L1[0;1] .
, X=L1[0;1] .
Решение.
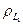 (xn , a) =
(xn , a) = 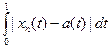 =
=  dt =
dt =  .
.
Применим теорему Беппо Леви о предельном переходе под знаком интеграла. Обозначим fn(t) =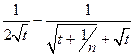 . Функция fn(t) является интегрируемой на [0;1] для любого
. Функция fn(t) является интегрируемой на [0;1] для любого 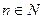 , и 0
, и 0 f1(x) ≤ f2(x) ≤ … ≤ fn(t) ≤ … . Кроме того,
f1(x) ≤ f2(x) ≤ … ≤ fn(t) ≤ … . Кроме того,  . Значит, по теореме Б. Леви
. Значит, по теореме Б. Леви

 (xn , a) =
(xn , a) = 
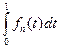 dt = 0.
dt = 0.
Следовательно, xn сходится к a в L1[0;1].
Пример 6 xn (t)=  , a(t) = t , X = L1[0;1] .
, a(t) = t , X = L1[0;1] .
Решение.
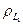 (xn , a) =
(xn , a) =  dt =
dt = 
 =
=  dt =
dt =
= 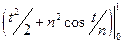 =
=  =
=  =
=
при 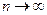 (мы воспользовались тем, что
(мы воспользовались тем, что 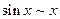 при
при  ). Значит, xn сходится к a в L1[0;1].
). Значит, xn сходится к a в L1[0;1].
Задача 2Является ли данное условие: а) необходимым, б) достаточным,
в) необходимым и достаточным для сходимости последовательности xn
в метрическом пространстве X ?
Пример 1 X = CL[a;b] – пространство непрерывных функций с метрикой
ρL(x , y) = 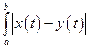 dt. Условие: последовательность xn(t) поточечно
dt. Условие: последовательность xn(t) поточечно
сходится к непрерывной функции a(t).
Решение. Не нарушая общности, можем считать, что a=0, b=1. Покажем, что условие не является ни необходимым, ни достаточным. Для выяснения достаточности условия рассмотрим следующую последовательность xn, заданную на [0;1] графически:

Последовательность xn сходится к a  0 поточечно на [0;1] (почему?), но
0 поточечно на [0;1] (почему?), но
ρL(xn , а) = 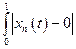 dt =
dt =  dt =
dt = 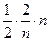 = 1,
= 1,
то есть ρL(xn , a) не стремится к нулю. Значит, данное условие не является достаточным для сходимости последовательности xn в метрическом пространстве CL[a;b].
Теперь допустим, что xn a в CL[0;1], то есть
a в CL[0;1], то есть  dt
dt 0 при
0 при 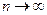 . Покажем на примере, что отсюда не следует поточечная сходимость xn к a. Рассмотрим последовательность xn(t) = tn и функцию a(t)
. Покажем на примере, что отсюда не следует поточечная сходимость xn к a. Рассмотрим последовательность xn(t) = tn и функцию a(t)  0. Имеем
0. Имеем
ρL(xn , а) = 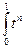 dt =
dt =  =
= 
 0 при
0 при 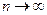 .
.
Значит, xn a=0 в CL[0;1]. Но tn не сходится к a= 0 поточечно, так как tn
a=0 в CL[0;1]. Но tn не сходится к a= 0 поточечно, так как tn 1 при t = 1. Значит, данное условие не является необходимым для сходимости последовательности xn в метрическом пространстве CL[a;b].
1 при t = 1. Значит, данное условие не является необходимым для сходимости последовательности xn в метрическом пространстве CL[a;b].
.
Пример 2 X = l2. Условие:  = 0, где
= 0, где  .
.
Решение. Положим  . Тогда данное условие означает, что
. Тогда данное условие означает, что  при
при 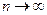 . Докажем, что это условие является достаточным для сходимости последовательности xn к а в пространстве l2. Поскольку при выполнении этого условия
. Докажем, что это условие является достаточным для сходимости последовательности xn к а в пространстве l2. Поскольку при выполнении этого условия 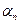 <1 при достаточно больших n, то при этих n и при всех k имеем
<1 при достаточно больших n, то при этих n и при всех k имеем 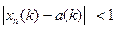 . Поэтому
. Поэтому 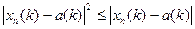 при этих n и при всех k. Значит, ρ2(xn , a)2
при этих n и при всех k. Значит, ρ2(xn , a)2
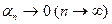 , а
, а
это значит, что ρ2(xn , a)  0. Следовательно, xn
0. Следовательно, xn a в l2. Достаточность доказана.
a в l2. Достаточность доказана.
Теперь покажем, что условие не является необходимым. Рассмотрим последовательность xn =  и точку a =
и точку a =  из l2. Имеем ρ2(xn , a) =
из l2. Имеем ρ2(xn , a) =  0 (
0 (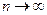 ) как остаток сходящегося ряда. Значит, xn
) как остаток сходящегося ряда. Значит, xn a в l2 . Но в этом примере
a в l2 . Но в этом примере 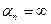 (сравните с гармоническим рядом), а потому данное условие не выполняется.
(сравните с гармоническим рядом), а потому данное условие не выполняется.
Задача 3Найти предел последовательности xn в метрическом пространстве X, если он
существует.
Пример 1 X = l1, xn =  .
.
Решение.1 способ. Допустим, xn сходится к некоторому a в l1. Так как для любого k справедливо неравенство  ρ1(xn , a)
ρ1(xn , a)  , то имеем и покоординатную сходимость xn к a. Но покоординатно xn сходится к последовательности
, то имеем и покоординатную сходимость xn к a. Но покоординатно xn сходится к последовательности 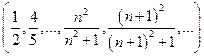 , которая не принадлежит пространству l1 (ряд
, которая не принадлежит пространству l1 (ряд  расходится по необходимому признаку). Мы пришли к противоречию. Значит, xn не сходится в l1.
расходится по необходимому признаку). Мы пришли к противоречию. Значит, xn не сходится в l1.
2 способ. Так как ρ1(xn , xn+1) =  1 при
1 при 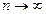 , последовательность xn не является фундаментальной. Следовательно, xn не сходится в l1.
, последовательность xn не является фундаментальной. Следовательно, xn не сходится в l1.
Пример 2X =  , xn =
, xn = 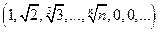 .
.
Решение. 1 способ. Допустим, xn сходится к некоторому a в  . Так как
. Так как 
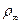 (xn , a)
(xn , a)  для любого k, то имеем покоординатную сходимость xn к a. Но покоординатно xn сходится к последовательности
для любого k, то имеем покоординатную сходимость xn к a. Но покоординатно xn сходится к последовательности
а=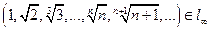 , для которой
, для которой 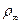 (xn , a) =
(xn , a) =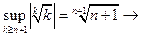 1 (почему?) при
1 (почему?) при 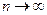 . Следовательно, xn не сходится к a в
. Следовательно, xn не сходится к a в  , - противоречие.
, - противоречие.
2 способ. Заметим, что последовательность xn не является фундаментальной в  . Действительно, xn+1 =
. Действительно, xn+1 = , ρ(xn , xn+1) =
, ρ(xn , xn+1) =  1 при
1 при 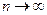 . Так как xn не фундаментальна в
. Так как xn не фундаментальна в  , то она не сходится в
, то она не сходится в  .
.
Задания лабораторной работы
Задача 1 Проверить, сходится ли заданная последовательность xn точек метрического
пространства X к точке a, если выполнены следующие условия.
а)
| № | X | xn | a |
| 1.1.1 | C[0;2] | 
| t |
| 1.1.2 | C[0;5] | 
| |
| 1.1.3 | C[-3;3] | 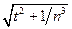
| | t | |
| 1.1.4 | C[0;8] | 
| t |
| 1.1.5 | C[0;1] | 
| t |
| 1.1.6 | C[1;2] | 
| 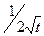
|
б)
| № | X | xn | a |
| 1.2.1 |

| 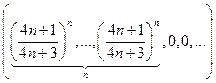
|
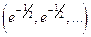
|
| 1.2.2 |
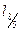
| 
|
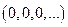
|
| 1.2.3 |
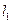
| 
|
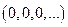
|
| 1.2.4 | 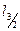
| 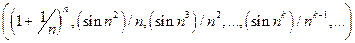
| 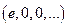
|
| 1.2.5 |

| 
|
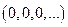
|
| 1.2.6 |

| 
|
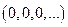
|
в)
| № | X | xn | a |
| 1.3.1 | L2[0;2] | 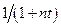
| |
| 1.3.2 | L4[0;3] | 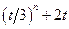
| 2t |
| 1.3.3 | 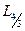 [-1;2] [-1;2]
| 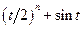
| sin t |
| 1.3.4 | L1[0;1] | 
| |
| 1.3.5 | 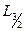 [-2;0] [-2;0]
| 
| 2t2 |
| 1.3.6 | L2[0;3] | 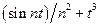
| t3 |
Задача 2 Является ли данное условие: а) необходимым, б) достаточным,
в) необходимым и достаточным для сходимости последовательности xn
в метрическом пространстве X ?
| № | X | Условие |
| 2.1 | C[a;b] |  t t [a;b] существует предел числовой последовательности xn(t) [a;b] существует предел числовой последовательности xn(t)
|
| 2.2 | 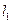
|  k k N существует предел числовой последовательности xn(k) N существует предел числовой последовательности xn(k)
|
| 2.3 | 
|  = 0, где a= = 0, где a=
|
| 2.4 | 
|  k k N существует предел числовой последовательности xn(k) N существует предел числовой последовательности xn(k)
|
| 2.5 | 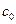
|  = 0, где a= = 0, где a=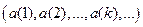
|
| 2.6 | 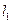
| 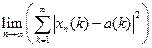 = 0, где a= = 0, где a=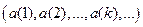
|
Задача 3 Найти предел последовательности xn в метрическом пространстве X, если он
существует.
| № | X | xn |
| 3.1 |

| 
|
| 3.2 |

| 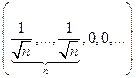
|
| 3.3 |

| 
|
| 3.4 |
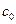
| 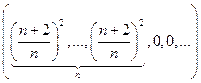
|
| 3.5 | 
| 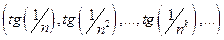
|
| 3.6 |
| 
|
Лабораторная работа 2
Топология метрических пространств
Примеры решения задач
Задача 1 Является ли данное множество  открытым, замкнутым, ограниченным в пространстве
открытым, замкнутым, ограниченным в пространстве . Найти его замыкание, внутренние и граничные точки.
. Найти его замыкание, внутренние и граничные точки.
Пример 1 
 .
.
Решение. Множество 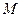 не является открытым, и более того, ни одна его точка не является внутренней. Действительно,
не является открытым, и более того, ни одна его точка не является внутренней. Действительно,  и для любого шара
и для любого шара  имеем
имеем  , но
, но  , так как
, так как 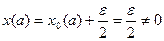 .
.
Множество 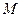 является замкнутым, так как оно содержит в себе пределы всех своих сходящихся последовательностей. Действительно, если
является замкнутым, так как оно содержит в себе пределы всех своих сходящихся последовательностей. Действительно, если  в
в  ,
, 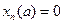 , то и
, то и  . А это значит, что
. А это значит, что  .
.
Граница множества 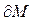 совпадает с самим множеством
совпадает с самим множеством 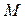 , что теперь сразу следует из формулы
, что теперь сразу следует из формулы 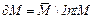 .
.
Множество  не является ограниченным, так как последовательность
не является ограниченным, так как последовательность 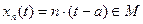 ,
,
но 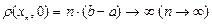 .
.
Пример 2 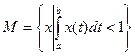 .
.
Решение. Покажем, что 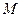 является открытым. Возьмём
является открытым. Возьмём 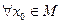 , т.е.
, т.е.  .
.
Тогда  . Покажем, что шар
. Покажем, что шар  . Возьмём
. Возьмём  .
.
Это значит, что  . Тогда
. Тогда
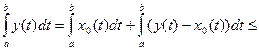
 .
.
Значит, 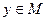 .
.
Так как М открыто, то  .
.
Множество М не является замкнутым, так как содержит не все свои предельные точки. Действительно, возьмём последовательность  из М. Тогда
из М. Тогда  , но
, но  , т.е.
, т.е.  .
.
Замечание. Нормированное пространство X всегда связно, так как любые две его точки х и у можно связать непрерывным путем  , лежащим в X, а потому в нем нет открытых и одновременно замкнутых собственных подмножеств.
, лежащим в X, а потому в нем нет открытых и одновременно замкнутых собственных подмножеств. 
Замыкание 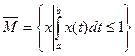 . Действительно, если x0 принадлежит
. Действительно, если x0 принадлежит 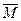 , то найдется последовательность
, то найдется последовательность  равномерно сходящаяся к
равномерно сходящаяся к 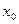 на [a,b]. А тогда
на [a,b]. А тогда
 .
.
Обратно, если 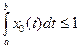 , то последовательность
, то последовательность 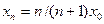 принадлежит М и сходится к х0 равномерно (проверьте!), а потому х0 принадлежит
принадлежит М и сходится к х0 равномерно (проверьте!), а потому х0 принадлежит 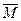 .
.
Теперь ясно, что граница
 .
.
Наконец, 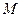 не является ограниченным, так как
не является ограниченным, так как 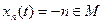 , но
, но 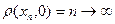 .
.
Пример 3 
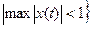 .
.
Решение. Покажем, что М открыто. Возьмём  . Тогда
. Тогда  , а потому
, а потому 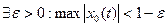 . Рассмотрим
. Рассмотрим 
 . Для любого
. Для любого  имеем
имеем  , а тогда
, а тогда  .
.
Покажем, что замыкание множества М есть 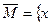
 . Действительно, если x0 принадлежит
. Действительно, если x0 принадлежит 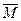 , то найдется последовательность
, то найдется последовательность равномерно сходящаяся к
равномерно сходящаяся к 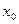 на [a,b]. А тогда
на [a,b]. А тогда 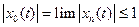 . Обратно, если
. Обратно, если 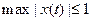 , то последовательность
, то последовательность 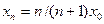 принадлежит М и сходится к
принадлежит М и сходится к 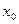 равномерно на [a,b] (проверьте), а потому
равномерно на [a,b] (проверьте), а потому 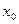 принадлежит
принадлежит 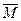 .
.
Теперь ясно, что граница 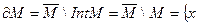
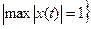 .
.
Очевидно, что данное множество ограничено.
Задача 2 Для данного множества А выяснить, является ли множество 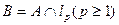 открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в  .
.
Пример 1 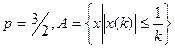 .
.
Решение. Множество 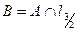 замкнуто, так как содержит в себе все свои предельные точки. Действительно, если
замкнуто, так как содержит в себе все свои предельные точки. Действительно, если 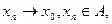 то
то 
 (почему?). Но так как
(почему?). Но так как  , то и
, то и  . Значит,
. Значит, 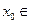 В.
В.
Так как В замкнуто, то оно не является открытым, поскольку  пространство
пространство  связно (см. замечание в решении примера 2 к задаче 1), но легко дать и прямое доказательство. Действительно, точка e1=(1,0,0,…) принадлежит В, но для любого
связно (см. замечание в решении примера 2 к задаче 1), но легко дать и прямое доказательство. Действительно, точка e1=(1,0,0,…) принадлежит В, но для любого 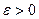 точка
точка  , хотя и лежит в
, хотя и лежит в 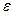 - окрестности точки
- окрестности точки  .
.
Наконец, В ограничено, так как 
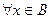
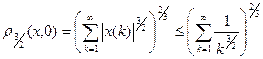 .
.
Пример 2 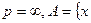
 .
.
Решение. Множество  не является открытым. Для доказательства покажем, что точка
не является открытым. Для доказательства покажем, что точка 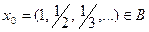 не является для него внутренней. Возьмём
не является для него внутренней. Возьмём  и найдём такое натуральное N, что
и найдём такое натуральное N, что  . Тогда
. Тогда 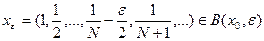 , но
, но  , поскольку
, поскольку 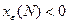 .
.
Множество В не замкнуто. Действительно, рассмотрим  . Тогда
. Тогда  сходится к точке
сходится к точке 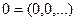 , так как
, так как  при
при  , но
, но 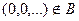 .
.
Множество В ограничено, так как 
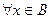 .
.
Пример 3 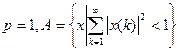 .
.
Решение. Покажем, что множество  открыто. Возьмём
открыто. Возьмём 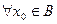 . Найдется такое
. Найдется такое 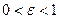 , что
, что  . Если
. Если 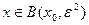 (шар рассматривается, конечно, в
(шар рассматривается, конечно, в 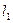 ), то
), то  . Тогда и
. Тогда и  . Теперь в силу неравенства Минковского имеем
. Теперь в силу неравенства Минковского имеем
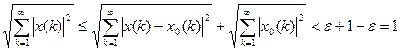 .
.
Значит,  , т.е.
, т.е. 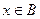 . Итак,
. Итак,  .
.
Так как В открыто, то В не замкнуто по замечанию из решения примера 2 к задаче 1. Дадим прямое доказательство этого факта. Точки  где
где 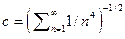 , очевидно, принадлежат В. В то же время,
, очевидно, принадлежат В. В то же время,  сходится в
сходится в 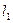 к
к  .
.
Покажем, что  не ограничено. Рассмотрим последовательность
не ограничено. Рассмотрим последовательность
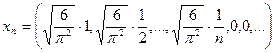 .
.
Имеем 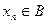 , так как
, так как
 ,
,
но в то же время  при
при  .
.
Пример 4  .
.
Решение. Покажем, что  не является открытым. Возьмём
не является открытым. Возьмём 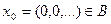 и
и  . Найдётся такое натуральное
. Найдётся такое натуральное  , что
, что  . Тогда
. Тогда 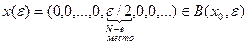 , но
, но  .
.
Множество В не является и замкнутым. Для доказательства рассмотрим последовательность 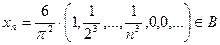 . Она сходится к точке
. Она сходится к точке  , которая не принадлежит В, так как
, которая не принадлежит В, так как 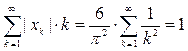 .
.
Множество В ограничено, поскольку неравенство 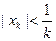 влечет
влечет
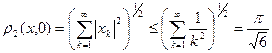 .
.
Задания лабораторной работы
Задача 1 Является ли данное множество М открытым, замкнутым, ограниченным в пространстве  ? Найти его замыкание, внутренние и граничные точки.
? Найти его замыкание, внутренние и граничные точки.
| № | М | № | М |
| 1.1 | 
| 1.4 |  
|
| 1.2 |  
| 1.5 |  
|
| 1.3 | 
| 1.6 | 
|
Задача 2 Для данного множества А выяснить, является ли множество 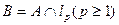 открытым, замкнутым, ограниченным в
открытым, замкнутым, ограниченным в  .
.
| № | 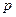
| А | № | 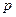
| А |
| 2.1 |  
| 2.4 | 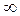
|  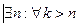 
| |
| 2.2 |  
| 2.5 | 3/2 |  
| |
| 2.3 |  
| 2.6 |  
|
Лабораторная работа 3
Полнота метрических пространств
Примеры решения задач
Задача 1 Является ли последовательность  фундаментальной в данном пространстве X? Найти
фундаментальной в данном пространстве X? Найти 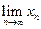 , если он существует.
, если он существует.
Пример 1  ,
,  ,
,
где K – канторово множество.
Решение. Так как канторово множество имеет лебегову меру нуль, то и  - множество меры нуль. Значит,
- множество меры нуль. Значит, 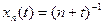 п.в.
п.в.
Покажем, что  сходится к 0 в
сходится к 0 в  . Для этого рассмотрим
. Для этого рассмотрим 
и воспользуемся разложением по формуле Тейлора:
 при
при 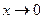 .
.
Получаем:
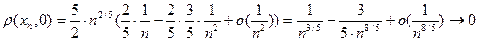 при
при 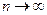 .
.
Тот же результат мы получим, применив теорему Лебега о предельном переходе под знаком интеграла.
Итак,  сходится к 0, а потому она фундаментальна.
сходится к 0, а потому она фундаментальна.
Пример 2  ,
,  ,
,
Решение. Так как 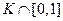 - множество меры нуль, то
- множество меры нуль, то 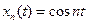 п.в. на [0;1]. Покажем, что эта последовательность не фундаментальна в нашем пространстве:
п.в. на [0;1]. Покажем, что эта последовательность не фундаментальна в нашем пространстве:

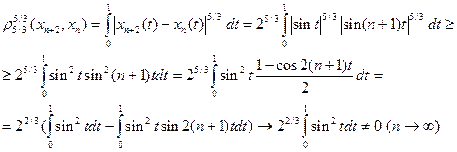
(мы воспользовались леммой Римана из теории рядов Фурье, согласно которой 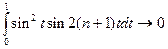 , но можно было бы вычислить интеграл и непосредственно).
, но можно было бы вычислить интеграл и непосредственно).
Задача 2 Является ли метрическое пространство 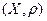 полным?
полным?
Пример 1Х=B[0,1] пространство вещественнозначных ограниченных функций на [0,1], наделенное метрикой

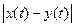 .
.
Решение. Покажем, что любая фундаментальная последовательность (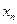 ) в B[0,1] является сходящейся. Ее фундаментальность значит, что
) в B[0,1] является сходящейся. Ее фундаментальность значит, что 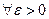
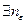 :
: 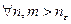 выполняется неравенство
выполняется неравенство

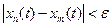 (1)
(1)
Зафиксируем произвольное число 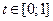 . Тогда числовая последовательность (
. Тогда числовая последовательность ( ) в силу (1) является фундаментальной в R. По причине полноты пространства Rпоследовательность
) в силу (1) является фундаментальной в R. По причине полноты пространства Rпоследовательность сходится. Положим
сходится. Положим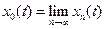 , t
, t [0,1]. Тем самым на [0;1] определена функция
[0,1]. Тем самым на [0;1] определена функция  , к которой
, к которой 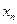 сходится поточечно. Осталось доказать, что
сходится поточечно. Осталось доказать, что
1) 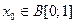 и 2)
и 2) 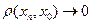 при
при 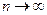 .
.
С этой целью перейдем в (1) (а точнее, в неравенстве 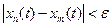 , справедливом при всех t из [0,1]) к пределу при
, справедливом при всех t из [0,1]) к пределу при 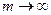 . Получим, что
. Получим, что
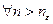

 (2)
(2)
В частности, при 
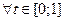 выполняется оценка:
выполняется оценка:
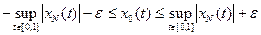 ,
,
из которой следует ограниченность  . Следовательно,
. Следовательно, 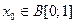 . Наконец, формула (2) означает, что
. Наконец, формула (2) означает, что 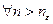
 . Поэтому
. Поэтому 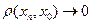 при
при 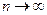 .
.
.
Пример 2  (
( ) – пространство числовых последовательностей
) – пространство числовых последовательностей  , удовлетворяющих условию:
, удовлетворяющих условию: 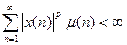 , где
, где  ,
,  ) заданная числовая последовательность;
) заданная числовая последовательность; 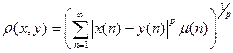 .
.
Решение. Покажем, что данное пространство полно. Пусть (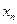 ) - фундаментальная последовательность в
) - фундаментальная последовательность в  . Это значит, что
. Это значит, что
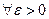
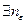 :
: 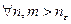
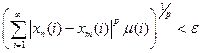 . (1)
. (1)
Тогда для любого фиксированного  имеем
имеем 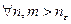
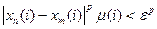 , т. е.
, т. е. 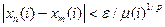 . Следовательно, для любого фиксированного
. Следовательно, для любого фиксированного  числовая последовательность
числовая последовательность 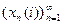 является фундаментальной, а потому сходится. Обозначим
является фундаментальной, а потому сходится. Обозначим  и положим
и положим 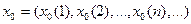 . Осталось показать, что
. Осталось показать, что
1) 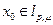 и
и
2) 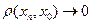 при
при 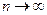 .
.
Из (1) следует, что 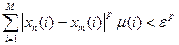 любого фиксированного
любого фиксированного 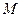 , что в пределе при
, что в пределе при 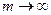 дает
дает 
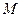
 . Переходя теперь к пределу при
. Переходя теперь к пределу при 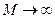 , получим
, получим 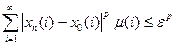 , т.е.
, т.е.
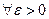
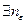 :
: 
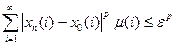 (2)
(2)
Возьмем какие-нибудь  и
и  и обозначим
и обозначим
 .
.
Вследствие неравенства Минковского имеем


 ,
,
а это значит, что 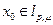 . Теперь (2) показывает, что
. Теперь (2) показывает, что 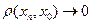 при
при 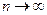 , а потому (
, а потому (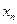 ) сходится в нашем пространстве к
) сходится в нашем пространстве к  .
.
Пример 3 Х=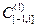 множество непрерывно дифференцируемых на [-1,1] функций с метрикой
множество непрерывно дифференцируемых на [-1,1] функций с метрикой  .
.
Решение. Рассмотрим последовательность 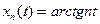 и покажем, что она является фундаментальной, но не является сходящейся в нашем пространстве. Заметим, что эта последовательность поточечно сходится к функции
и покажем, что она является фундаментальной, но не является сходящейся в нашем пространстве. Заметим, что эта последовательность поточечно сходится к функции  Х., где
Х., где
 .
.
А так как  , то по теореме Лебега
, то по теореме Лебега  при
при 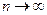 . Это означает, что в пространстве
. Это означает, что в пространстве  последовательность
последовательность 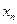 сходится к
сходится к  . Следовательно, она фундаментальна в Х. С другой стороны, если предположить, что последовательность
. Следовательно, она фундаментальна в Х. С другой стороны, если предположить, что последовательность 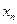 сходится в данном пространстве Х к некоторой функции
сходится в данном пространстве Х к некоторой функции  , то получим, что
, то получим, что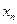 имеет два предела в
имеет два предела в 
 и
и  , противоречие. Итак, данное пространство не является полным.
, противоречие. Итак, данное пространство не является полным.
Задания лабораторной работы
Задача 1 Является ли последовательность  фундаментальной в данном пространстве X? Найти
фундаментальной в данном пространстве X? Найти 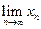 , если он существует.
, если он существует.
| № | X | 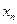
| № | X | 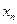
|
| 1.1 |
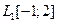
| 
| 1.4 | 
| 
|
| 1.2 | 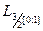
| 
| 1.5 | 
| 
|
| 1.3 | 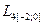
| 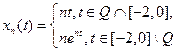
| 1.6 | 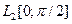
| 
|
Задача 2 Выяснить, является ли заданное пространство 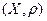 полным.
полным.
2.1 А) Пространство  непрерывно дифференцируемых на отрезке [a;b] функций с метрикой
непрерывно дифференцируемых на отрезке [a;b] функций с метрикой  .
.
Б) Пространство всех дважды дифференцируемых на отрезке [a;b] функций с метрикой 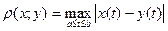 .
.
2.2 А) Пространство 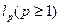 числовых последовательностей
числовых последовательностей 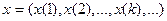 , удовлетворяющих условию
, удовлетворяющих условию 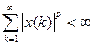 , с метрикой
, с метрикой 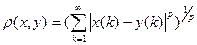 .
.
Б) Пространство всех непрерывных на отрезке [a;b] функций с метрикой 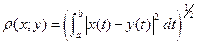 .
.
2.3 А) Пространство  всех ограниченных числовых последовательностей
всех ограниченных числовых последовательностей 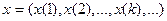 с метрикой
с метрикой  .
.
Б)  с метрикой
с метрикой 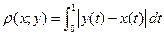 .
.
2.4 А) Пространство 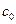 сходящихся к нулю последовательностей
сходящихся к нулю последовательностей 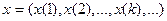 с метрикой
с метрикой  .
.
Б)  с метрикой
с метрикой  .
.
2.5 А) Пространство с сходящихся последовательностей 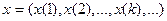 с метрикой
с метрикой  .
.
Б)  , с метрикой
, с метрикой  .
.
2.6 А) Пространство  ограниченных и непрерывных на интервале (a;b) функций с метрикой
ограниченных и непрерывных на интервале (a;b) функций с метрикой 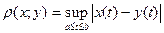 .
.
Б) 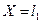 с метрикой
с метрикой  .
.
Лабораторная работа 4
Примеры решения задачЛабораторная работа 5
Компактные множества в метрических пространствах
Примеры решения задач
Задача 1 Выяснить, являются ли данные множества предкомпактными,
компактными в C[0;1].
Пример 1 а) М = {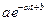 | a,b,α
| a,b,α  [0;1]};
[0;1]};
б) М1 = {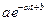 | a,b
| a,b  [0;1], α
[0;1], α  (0;1)}.
(0;1)}.
Решение. Проверим для множества М условия теоремы Арцела-Асколи. Рассмотрим функцию f(t,a,b,α) = 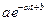 . Пусть К = [0;1]3. Тогда f непрерывна на [0;1]
. Пусть К = [0;1]3. Тогда f непрерывна на [0;1] К и М=
К и М=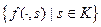 . Множество [0;1]
. Множество [0;1] К является компактом. По теореме Вейерштрасса f ограничена на [0;1]
К является компактом. По теореме Вейерштрасса f ограничена на [0;1] К, т.е.
К, т.е.  с
с  t
t [0;1]
[0;1]  (a,b,α)
(a,b,α)  [0;1]3 справедливо неравенство
[0;1]3 справедливо неравенство 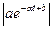
 c. Значит, М равномерно ограничено (впрочем, легко проверить и непосредственно, что при наших условиях
c. Значит, М равномерно ограничено (впрочем, легко проверить и непосредственно, что при наших условиях 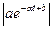
 1).
1).
Проверим равностепенную непрерывность множества М. По теореме Кантора f равномерно непрерывна на [0;1] К. Если обозначить через s = (a,b,α) произвольную точку из К, то равномерная непрерывность f означает, что
К. Если обозначить через s = (a,b,α) произвольную точку из К, то равномерная непрерывность f означает, что  >0
>0 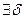 >0
>0 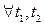 из [0;1], таких, что |t1 - t2| <
из [0;1], таких, что |t1 - t2| < , и
, и 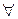 s1,s2 из К, таких, что ρ(s1,s2) <
s1,s2 из К, таких, что ρ(s1,s2) < (ρ обозначает евклидову метрику в К), справедливо неравенство
(ρ обозначает евклидову метрику в К), справедливо неравенство
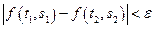 .
.
Отсюда следует равностепенная непрерывность множества М (см. определение). Значит, по теореме Арцела-Асколи М предкомпактно.
Для доказательства компактности множества М теперь достаточно проверить его замкнутость в C[0;1]. Но это тоже следует из непрерывности функции f. В самом деле, если х предельная точка множества М, то найдется последовательность  функций из М, сходящаяся к х в C[0;1]. По свойству Больцано-Вейерштрасса из последовательности sn точек множества К можно выбрать подпоследовательность
функций из М, сходящаяся к х в C[0;1]. По свойству Больцано-Вейерштрасса из последовательности sn точек множества К можно выбрать подпоследовательность  , сходящуюся к точке
, сходящуюся к точке 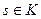 . Тогда поточечно
. Тогда поточечно  , а потому в силу единственности предела
, а потому в силу единственности предела 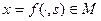 . Итак, М – компакт.
. Итак, М – компакт.
Далее, так как М1  М, то множество М1 предкомпактно. Но М1 не является компактом, так как не замкнуто в C[0;1]. Действительно, функции хn(t) =
М, то множество М1 предкомпактно. Но М1 не является компактом, так как не замкнуто в C[0;1]. Действительно, функции хn(t) = 
 М1, но предел этой последовательности х0(t) = 1
М1, но предел этой последовательности х0(t) = 1 М1.
М1.
Пример 2 М = {tn | n N}.
N}.
Решение. Это множество является равномерно ограниченным, но не является равностепенно непрерывным. Действительно, возьмем 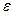 = 1/4. Тогда
= 1/4. Тогда  >0 найдется такое натуральное n, что точки t1=1 и t2 =
>0 найдется такое натуральное n, что точки t1=1 и t2 =
 [0;1] удовлетворяют неравенству |t1 - t2| =
[0;1] удовлетворяют неравенству |t1 - t2| = 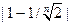 <
< , но в то же время
, но в то же время  =
=  >
>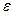 . Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
. Значит, по теореме Арцела-Асколи М не является предкомпактным, а потому и компактным множеством.
Пример 3 М = {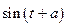 | a
| a R}.
R}.
Решение. Множество М равномерно ограничено, так как
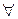 t
t 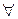 a
a
 1.
1.
Множество М равностепенно непрерывно, так как 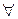
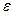 >0
>0 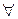 a
a R и
R и 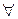 t1, t2
t1, t2 [0;1], таких, что |t1 - t2| <
[0;1], таких, что |t1 - t2| <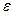 , имеем
, имеем
| | =
| = 
 |t1 - t2| <
|t1 - t2| <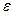 .
.
Значит, по теореме Арцела-Асколи М предкомпактно.
Покажем, что М содержит все свои предельные точки. Пусть х есть предельная точка множества М, 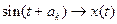 равномерно на [0;1]. В силу периодичности синуса можно считать, что
равномерно на [0;1]. В силу периодичности синуса можно считать, что  . При этом промежуток
. При этом промежуток  удобно отождествлять с факторгруппой R/
удобно отождествлять с факторгруппой R/ Z, т. е. с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность
Z, т. е. с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность  в R сходится к
в R сходится к  , то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует
, то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует  . Действительно, если допустить противное, то найдутся две подпоследовательности
. Действительно, если допустить противное, то найдутся две подпоследовательности  и
и  , имеющие различные пределы a’ и a’’
, имеющие различные пределы a’ и a’’ соответственно. Но тогда
соответственно. Но тогда 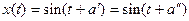 , откуда a’ = a’’, противоречие. Следовательно,
, откуда a’ = a’’, противоречие. Следовательно,  . Значит, М – замкнутое множество, откуда следует, что М – компакт.
. Значит, М – замкнутое множество, откуда следует, что М – компакт.
Задача 2 Является ли множество М предкомпактным в l1?
Пример 1 M = {x l1 | |
l1 | | | <
| < , |
, | | <
| <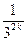 , |
, |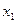 | = 1}.
| = 1}.
Решение. Проверим критерий предкомпактности в l1
1). Множество М является ограниченным, поскольку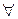 n
n 2 |xn | <
2 |xn | < , а потому
, а потому
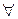 х
х М
М 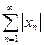 < 1 +
< 1 + 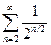 =
= .
.
2) Так как ряд  сходится, то его остаток стремится к нулю, т.е.
сходится, то его остаток стремится к нулю, т.е.
 >0
>0  N :
N :  <
<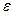 .
.
Поэтому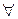
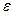 >0
>0  N:
N: 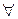 х
х М
М 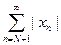 <
< <
<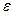 .
.
Значит, множество М предкомпактно.
Задания лабораторной работы
Задача 1 Выяснить, является ли множество М предкомпактным, компактным в C[0;1].
| № | М | № | М |
| 1.1 | {atα | 1 α α 10, |a| 10, |a| 10} 10}
| 1.4 | {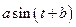 ) | 0 ) | 0 a, b a, b 1} 1}
|
| 1.2 | {atα | 0 α α 1, 0 < a < 1} 1, 0 < a < 1}
| 1.5 | {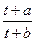 | 1 | 1 a, b a, b 2} 2}
|
| 1.3 | {cos at | -1 a a 1} 1}
| 1.6 | { 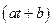 | a | a 1, b>1} 1, b>1}
|
Задача 2 Является ли множество М предкомпактным в lp?
| № | р | М |
| 2.1 | {x| | xk | <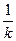 , k , k N} N}
| |
| 2.2 | {x |  < | xk | < < | xk | < , k , k N } N }
| |
| 2.3 | {x | | xk |   , k , k N } N }
| |
| 2.4 | {x |   | xk | | xk |   , k , k N } N }
| |
| 2.5 | {x | x2k = 0, 0 < x2k+1   , k , k N } N }
| |
| 2.6 | {x | | xk | < , , 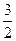  α α   } }
|
Лабораторная работа 6
Сжимающие отображения
Примеры решения задач
Задача 1Является ли отображение F метрического пространства X в себя сжимающим?
Найти х3, где хк+1 = F(хк), х0 = 0. Оценить расстояние от х3 до неподвижной
точки, если F является сжимающим.
Пример 1 .
Решение. Оценим расстояние в 


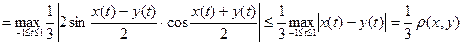
(мы воспользовались неравенством 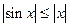 ). Значит, F является сжимающим отображением с константой Липшица
). Значит, F является сжимающим отображением с константой Липшица
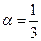 .
.
Построим последовательность  . По условию
. По условию 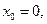 поэтому
поэтому 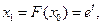
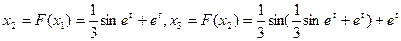 . А так как
. А так как
 ,
,
где  - неподвижная точка, то
- неподвижная точка, то
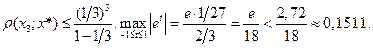
Пример 2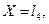

Решение. Оценим расстояние в 

Значит, f – сжимающее отображение с константой 
По условию,  . Тогда
. Тогда 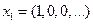 ,
, 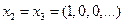 , а потому
, а потому
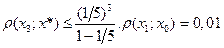
(на самом деле, как легко проверить, 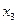 является неподвижной точкой).
является неподвижной точкой).
Пример 3 .
Решение. Допустим, что отображение F является сжимающим, т.е.
 .
.
При y=0 из этого неравенства следует, что 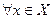
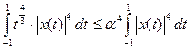 . (1)
. (1)
Подставив  в левую часть неравенства (1), получим
в левую часть неравенства (1), получим
 при
при 
(мы воспользовались эквивалентностью  при
при 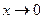 ).
).
Правая же часть неравенства (1), как легко проверить, при этом значении х равна  . Следовательно, неравенство (1) при указанных
. Следовательно, неравенство (1) при указанных  и
и  примет вид:
примет вид: 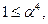 противоречие. Значит, F не является сжимающим. (Аналогичное решение получается и при
противоречие. Значит, F не является сжимающим. (Аналогичное решение получается и при  ).
).
Задача 2Применим ли принцип сжимающих отображений к заданному интегральному
уравнению в пространстве Х при 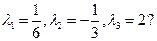 При
При  с точностью до
с точностью до
0,01 найти приближенное решение и сравнить его с точным решением.
 (1)
(1)
Решение. Определим отображение  по формуле
по формуле
 (2)
(2)
Тогда исходное уравнение запишется в виде  и искомое решение есть неподвижная точка отображения
и искомое решение есть неподвижная точка отображения 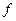 . Метрическое пространство C[0;1] является полным, поэтому если мы покажем, что
. Метрическое пространство C[0;1] является полным, поэтому если мы покажем, что 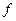 – сжимающее отображение C[0;1] в себя, то можно будет применить принцип сжимающих отображений. То, что отображение
– сжимающее отображение C[0;1] в себя, то можно будет применить принцип сжимающих отображений. То, что отображение 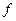 непрерывную на
непрерывную на  функцию переводит в непрерывную, в данном случае очевидно (а в общем следует из свойств интеграла, зависящего от параметра). Определим, при каких
функцию переводит в непрерывную, в данном случае очевидно (а в общем следует из свойств интеграла, зависящего от параметра). Определим, при каких  отображение
отображение 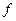 является сжимающим. Известно, что отображение
является сжимающим. Известно, что отображение
 (3)
(3)
является сжимающим в C[a;b], если  где
где  . При этом константа Липшица
. При этом константа Липшица 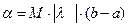 . (Заметим, что это утверждение дает лишь достаточное условие сжимаемости). В данном случае
. (Заметим, что это утверждение дает лишь достаточное условие сжимаемости). В данном случае 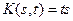 ,
, 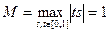 . Следовательно,
. Следовательно, 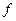 является сжимающим при
является сжимающим при  т.е., в частности, при
т.е., в частности, при  и
и  .
.
Докажем, что 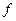 не является сжимающим при
не является сжимающим при 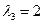 . Если допустить, что
. Если допустить, что 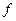 – сжимающее, то для
– сжимающее, то для 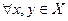 и некоторого
и некоторого  должно выполняться неравенство
должно выполняться неравенство
 .
.
При  ,
, 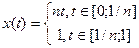 последнее неравенство примет вид
последнее неравенство примет вид  . А так как
. А так как 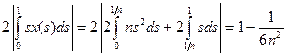 ,
,
То получаем, что  , откуда в пределе
, откуда в пределе 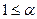 . Это противоречие доказывает, что
. Это противоречие доказывает, что 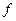 не является сжимающим при
не является сжимающим при  .
.
Решим уравнение (1) при  . При этом
. При этом  отображение
отображение 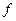 - сжимающее, а потому для нахождения приближённого решения можно воспользоваться методом итераций (последовательных приближений). Из уравнения (1) следует, что его решение имеет вид
- сжимающее, а потому для нахождения приближённого решения можно воспользоваться методом итераций (последовательных приближений). Из уравнения (1) следует, что его решение имеет вид
 где
где 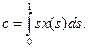 (4)
(4)
Поскольку  выбирается произвольно, возьмём
выбирается произвольно, возьмём  . Дальнейшие приближения находятся по формулам
. Дальнейшие приближения находятся по формулам  ,
,  .
.
Установим номер k, при котором элемент  будет давать точность приближения 0,01. Используем оценку погрешности (х - точное решение)
будет давать точность приближения 0,01. Используем оценку погрешности (х - точное решение)
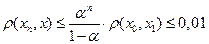 .
.
В нашем случае  . Тогда
. Тогда
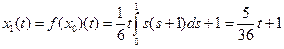 .
.
 .
.
Следовательно,
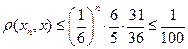 ,
,
А потому искомое k определяется из неравенства: 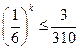 . Поскольку k=3 ему удовлетворяет,
. Поскольку k=3 ему удовлетворяет, 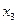 будет приближенным решением исходного уравнения с точностью 0,01. Найдём
будет приближенным решением исходного уравнения с точностью 0,01. Найдём 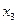 :
:
 ,
,
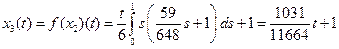 .
.
Итак, приближённое решение с нужной точностью есть 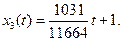
Точное решение имеет вид 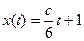 (см. формулу (4)). Подставив
(см. формулу (4)). Подставив 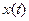 в (1), получим:
в (1), получим:
 . Отсюда
. Отсюда  ,
, 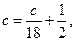
 . Следовательно, точное решение есть
. Следовательно, точное решение есть

Сравним его с приближённым:
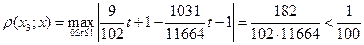 .
.
Замечание.Первую часть решения можно сократить, если воспользоваться тем фактом, что норма линейного оператора
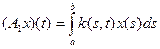
в пространстве C[0;1] дается формулой
 .
.
Поскольку норма есть точная константа в неравенстве ограниченности, отображение А1 является сжимающим тогда и только тогда, когда 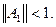 То же верно и для отображения
То же верно и для отображения 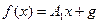 (почему?).
(почему?).
Задания лабораторной работы
Задача 1Является ли отображение F метрического пространства X в себя сжимающим?
Найти х3, где хк+1 = F(хк), х0 = 0. Оценить расстояние от х3 до неподвижной
точки, если F является сжимающим.
| № | X | F |
| 1.1 | 
| 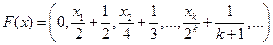
|
| 1.2 | 
| 
|
| 1.3 | C[-1;1] | 
|
| 1.4 | 
| 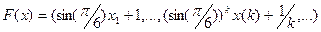
|
| 1.5 | C[-1;1] | 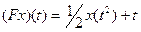
|
| 1.6 | 
| 
|
Задача 2 Применим ли принцип сжимающих отображений к заданному интегральному
уравнению в пространстве Х при 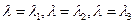 ? При
? При  с точностью
с точностью
до 0,01 найти приближённое решение и сравнить его с точным решением.
| № | Х | 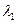
| 
| 
| Уравнение |
| 2.1 | C[0;1] | 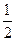
| 
| 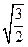
| 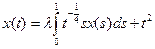
|
| 2.2 | C[-1;1] | 
| 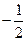
| 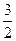
| 
|
| 2.3 | C[-2;2] | 
| 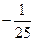
| 
| 
|
| 2.4 | C[-1;1] | 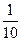
| 
| 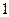
| 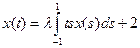
|
| 2.5 | C[0;1] | 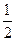
| 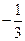
| 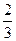
| 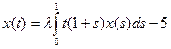
|
| 2.6 | C[-1;1] | 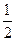
| 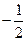
| 
| 
|
Лабораторная работа 7
Линейные нормированные пространства
Примеры решения задач
Задача 1 Является ли множество А выпуклым в пространстве Х?
Пример 1 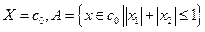

Решение. Воспользуемся определением выпуклости. Возьмем  и покажем, что
и покажем, что 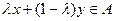 . Действительно, так как
. Действительно, так как 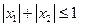 и
и  , то
, то
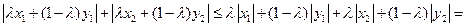

Значит, множество А является выпуклым.
Задача 2 Проверить, является ли заданная система векторов 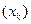 в бесконечномерном
в бесконечномерном
пространстве Х линейно независимой.
Пример 1 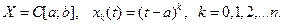
Решение. Покажем по определению, что система 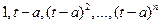 является линейно независимой. Пусть
является линейно независимой. Пусть
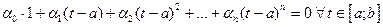 . (1)
. (1)
Подставив в это равенство t=a, получим  , а потому
, а потому
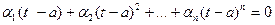 .
.
Сокращая на  и снова полагая t=a, получим
и снова полагая t=a, получим 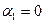 . Продолжая этот процесс, окончательно будем иметь
. Продолжая этот процесс, окончательно будем иметь 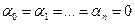 .
.
Второе решение: алгебраическое уравнение (1) не может иметь более n корней, если не все его коэффициенты равны нулю (почему?).
Пример 2 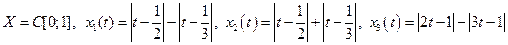 .
.
Решение. Заметим, что  .
.
Тогда 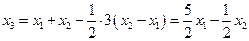 , а значит, данные функции линейно зависимы.
, а значит, данные функции линейно зависимы.
Задача 3 Привести пример последовательности  , сходящейся в Х, но не
, сходящейся в Х, но не
сходящейся в Y, если пространства Х и Y наделены естественными нормами.
Пример 1 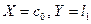 .
.
Решение. Рассмотрим последовательность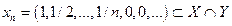 . В пространстве
. В пространстве 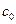 она сходится к вектору
она сходится к вектору  , так как
, так как
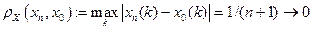
при 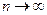 . Допустим, что
. Допустим, что  . Так как
. Так как
 ,
,
то 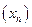 сходится к а и в пространстве
сходится к а и в пространстве 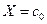 . В силу единственности предела отсюда следует, что
. В силу единственности предела отсюда следует, что 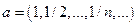 . Но
. Но 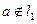 . Это противоречие доказывает, что в
. Это противоречие доказывает, что в 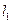 данная последовательность не сходится.
данная последовательность не сходится.
Пример 2 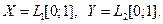
Решение. Рассмотрим последовательность  , которая
, которая  .
.
Тогда в  имеем
имеем 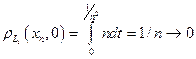 при
при 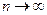 , т. е.
, т. е.  в
в  .
.
Допустим, что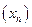 сходится в
сходится в  к некоторому
к некоторому  . В силу неравенства Коши-Буняковского
. В силу неравенства Коши-Буняковского
 .
.
Отсюда следует, что если 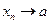 в
в , то
, то 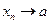 и в
и в  . В силу единственности предела, а=0. С другой стороны, легко проверить, что
. В силу единственности предела, а=0. С другой стороны, легко проверить, что  , противоречие. Следовательно, в
, противоречие. Следовательно, в  данная последовательность не сходится.
данная последовательность не сходится.
Пример 3 
Решение. Рассмотрим последовательность 
 . В
. В  имеем
имеем  , но в
, но в 
 0 (
0 (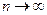 ). Значит,
). Значит, 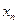
 0 в
0 в 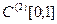 . Воспользовавшись неравенством:
. Воспользовавшись неравенством:  и рассуждая, как в предыдущих примерах, получим, что
и рассуждая, как в предыдущих примерах, получим, что 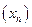 не сходится в
не сходится в 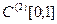 .
.
Задача 4 Выяснить, являются ли нормы p и q эквивалентными в данном пространстве X.
Пример 1
Решение. Очевидно, 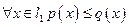 . Допустим теперь, что
. Допустим теперь, что
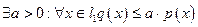 , т.е.
, т.е.  .
.
При  последнее неравенство примет вид:
последнее неравенство примет вид: 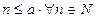 . Полученное противоречие доказывает, что p и q не эквивалентны.
. Полученное противоречие доказывает, что p и q не эквивалентны.
Пример 2 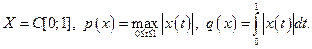
Решение. Заметим, что 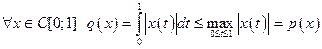 . Допустим, что
. Допустим, что  , т.е.
, т.е.  , и положим здесь
, и положим здесь 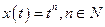 . Тогда последнее неравенство примет вид
. Тогда последнее неравенство примет вид 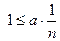 , т. е.
, т. е. 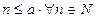 . Полученное противоречие показывает, что нормы p и q не эквивалентны.
. Полученное противоречие показывает, что нормы p и q не эквивалентны.
Пример 3 
Решение. Так как  , то
, то 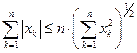 , т.е.
, т.е. 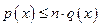 . С другой стороны, так как
. С другой стороны, так как 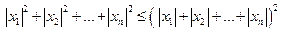 , то
, то 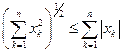 , т.е.
, т.е.  . Итак, мы доказали, что p и q – эквивалентные нормы.
. Итак, мы доказали, что p и q – эквивалентные нормы.
Пример 4 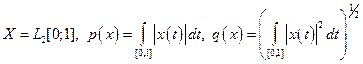 .
.
Решение. В силу неравенства Коши-Буняковского 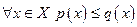 . Допустим, что
. Допустим, что  .
.
Возьмем  . Тогда
. Тогда 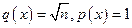 , и последнее неравенство примет вид:
, и последнее неравенство примет вид:  , что невозможно ни при каком a. Значит, нормы p и q не эквивалентны.
, что невозможно ни при каком a. Значит, нормы p и q не эквивалентны.
Задача 5 Построить изоморфизм между факторпространством L/M и одним из стандартных линейных пространств.
Пример 1 
Решение. Возьмем произвольный элемент  . Его класс эквивалентности есть
. Его класс эквивалентности есть

 .
.
Это равенство показывает, что отображение  инъективно. Очевидно также, что оно линейно и является сюръекцией (проверьте). Значит, f – изоморфизм линейных пространств.
инъективно. Очевидно также, что оно линейно и является сюръекцией (проверьте). Значит, f – изоморфизм линейных пространств.
Задания лабораторной работы
Задача 1Проверить, является ли функция p нормой в пространстве X. Образует ли пара
 , где
, где  , метрическое пространство?
, метрическое пространство?
| № | X | p(x) |
| 1.1 | 
| 
|
| 1.2 | 
| 
|
| 1.3 | 
| 
|
| 1.4 | 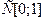
| 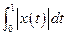
|
| 1.5 | 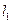
| 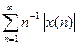
|
| 1.6 | 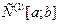
| 
|
Задача 2Является ли множество А выпуклым в пространстве X?
| № | X | A |
| 2.1 | 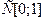
| неубывающие функции |
| 2.2 | 
| 
|
| 2.3 | 
| многочлены степени n |
| 2.4 | 
| 
|
| 2.5 | 
| многочлены степени  k k
|
| 2.6 | 
| 
|
Задача 3 Проверить, является ли данная последовательность векторов  в бесконечномерном пространстве X линейно независимой.
в бесконечномерном пространстве X линейно независимой.
| № | X | 
|
| 3.1 | 
| 
|
| 3.2 | 
| 
|
| 3.3 | 
| 
|
| 3.4 | 
| 
|
| 3.5 | 
|  -
функция Дирихле -
функция Дирихле
|
| 3.6 | 
| 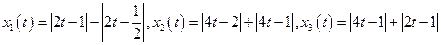
|
Задача 4 Привести пример последовательности  , которая сходится в X, но не сходится в Y, если пространства X и Y наделены естественными нормами.
, которая сходится в X, но не сходится в Y, если пространства X и Y наделены естественными нормами.
| № | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 |
| X | 
| 
| 
| 
| 
| 
|
| Y | 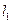
| 
| 
| 
| 
| 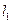
|
Задача 5 Являются ли нормы p и q эквивалентными в пространстве E?
| № | E | p | q |
| 5.1 |

|

| 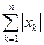 
|
| 5.2 |

|
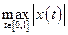
| 
|
| 5.3 |

| 
| 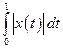
|
| 5.4 | c | 
| 
|
| 5.5 |
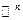
| 
| 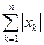
|
| 5.6 | 
| 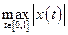
|  
|
Задача 6 Построить изоморфизм между факторпространством L/M и одним из стандартных линейных пространств.
| № | L | M |
| 6.1 |  
| 
|
| 6.2 | 
| 
|
| 6.3 | 
| 
|
| 6.4 | 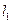
| 
|
| 6.5 |  
| 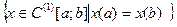
|
| 6.6 | 
| 
|
Лабораторная работа 8
Линейные ограниченные операторы в банаховых
Пространствах
Примеры решения задач
Задача 1Пусть X,Y – нормированные пространства. Выяснить, совпадает ли область
определения 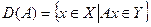 оператора А с нормированным простран-
оператора А с нормированным простран-
ством Х. Является ли оператор А линейным, непрерывным оператором из
D(A) в Y?
Пример 1  .
.
Решение. Если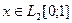 , то
, то  :=
:=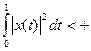
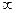 . В силу неравенства Коши-Буняковского
. В силу неравенства Коши-Буняковского
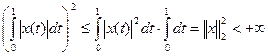 . (1)
. (1)
Отсюда следует, что  . Поэтому D(A)=X.
. Поэтому D(A)=X.
Оператор А не является линейным (рассмотрите, например,  ). Исследуем его на непрерывность. Для любой точки
). Исследуем его на непрерывность. Для любой точки 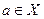 оценим расстояние
оценим расстояние


(мы воспользовались числовым неравенством  , а затем неравенством (1)). Поэтому
, а затем неравенством (1)). Поэтому 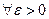 получаем при
получаем при 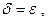 что
что  . Значит, оператор A непрерывен на
. Значит, оператор A непрерывен на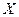 .
.
Пример 2  .
.
Решение. В этом примере D(a)≠X, так как  , но
, но  (в обоих случаях сходимость ряда исследуется с помощью интегрального признака; проделайте это). Очевидно, A является линейным оператором, поэтому исследование непрерывности равносильно исследованию ограниченности. Докажем, что A не является ограниченным. Допустим противное, то есть что
(в обоих случаях сходимость ряда исследуется с помощью интегрального признака; проделайте это). Очевидно, A является линейным оператором, поэтому исследование непрерывности равносильно исследованию ограниченности. Докажем, что A не является ограниченным. Допустим противное, то есть что  . При
. При  последнее неравенство примет вид
последнее неравенство примет вид
 , т.е.
, т.е. 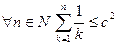 .
.
Поскольку частичные суммы ряда 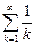
 не являются ограниченными, мы пришли к противоречию. Значит, A не является непрерывным.
не являются ограниченными, мы пришли к противоречию. Значит, A не является непрерывным.
Пример 3  .
.
Решение. Здесь D(A)≠X, так как последовательность  но
но 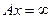 . Далее, оператор A не является линейным (как в примере 1). Докажем, что он не является непрерывным. Действительно, возьмём следующую последовательность
. Далее, оператор A не является линейным (как в примере 1). Докажем, что он не является непрерывным. Действительно, возьмём следующую последовательность  точек из
точек из 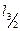 :
:
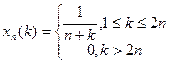 .
.
Тогда  в
в 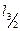 , так как
, так как
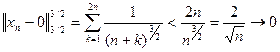 при
при  .
.
В то же время
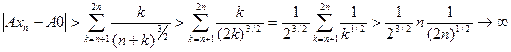 .
.
Таким образом, из того, что  , не следует, что
, не следует, что  . Мы показали, что А не является непрерывным в нуле, значит, A не является непрерывным на D(A).
. Мы показали, что А не является непрерывным в нуле, значит, A не является непрерывным на D(A).
Пример 4  .
.
Решение. Очевидно, что D(A)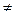 X и что A - нелинейный. Покажем, что A не является непрерывным в нуле. Возьмём последовательность
X и что A - нелинейный. Покажем, что A не является непрерывным в нуле. Возьмём последовательность  из C[0;1]. Она сходится к 0, так как
из C[0;1]. Она сходится к 0, так как 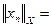
 при n→∞. Но в то же время
при n→∞. Но в то же время
 при n→∞.
при n→∞.
Т.е. из того, что  , не следует, что
, не следует, что 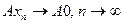 Значит, A не является непрерывным на D(A).
Значит, A не является непрерывным на D(A).
Задача 2 Доказать, что оператор  является линейным ограниченным, и
является линейным ограниченным, и
найти его норму.
а) Оператор умножения, действующий из X в Y.
Пример 1  .
.
Решение. Ясно, что A линейный.
Так как
 , (2)
, (2)
то A ограничен с константой ограниченности 1/2. А так как норма оператора есть наименьшая из констант ограниченности, то  .
.
Докажем теперь противоположное неравенство, т.е. что  . Для этого постараемся подобрать такой ненулевой вектор х0, для которого неравенство (2) превращается в равенство. Возьмём
. Для этого постараемся подобрать такой ненулевой вектор х0, для которого неравенство (2) превращается в равенство. Возьмём  . Тогда, как легко подсчитать,
. Тогда, как легко подсчитать,  .А так как
.А так как 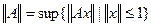 , то
, то  . Сопоставляя полученные неравенства, заключаем, что
. Сопоставляя полученные неравенства, заключаем, что 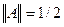 .
.
б) Диагональный оператор, действующий из  в
в  .
.
Пример 1 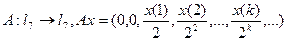 .
.
Решение. Ясно, что A - линейный оператор. Так как
 ,
,
то оператор A ограничен, причем  . Возьмём
. Возьмём  . Тогда
. Тогда 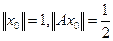 . Значит,
. Значит, 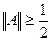 (почему?). Из полученных неравенств следует, что
(почему?). Из полученных неравенств следует, что 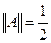 .
.
Пример 2  .
.
Решение. Оператор A - линейный. Докажем неравенство ограниченности:
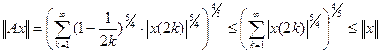 . (3)
. (3)
Значит, оператор А ограничен, причем  .
.
В отличие от предыдущих примеров, здесь не существует ненулевого вектора, при котором неравенство (3) превращается в равенство (подумайте, почему). Поэтому будем подбирать ненулевые векторы х так, чтобы обе части (3) мало отличались друг от друга. Возьмём 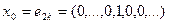 (единица стоит на 2k-м месте). Тогда имеем
(единица стоит на 2k-м месте). Тогда имеем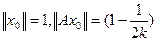 , откуда
, откуда 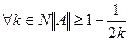 (см. решение примера 1). Ввиду произвольности k отсюда следует, что
(см. решение примера 1). Ввиду произвольности k отсюда следует, что  . Окончательно получаем, что
. Окончательно получаем, что  .
.
в) Оператор замены переменной.
Пример 1 .
Решение. Oчевидно, что оператор A линеен. Докажем его ограниченность:
 , (4)
, (4)
поскольку, как легко проверить,  =1/4. Следовательно,
=1/4. Следовательно,  . Далее, так как при
. Далее, так как при  неравенство (4) превращается в равенство, то
неравенство (4) превращается в равенство, то 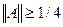 (см. решения предыдущих примеров). Итак,
(см. решения предыдущих примеров). Итак,  .
.

Пример 2  .
.
Решение. Oчевидно, что оператор A линеен. Докажем его ограниченность:

=
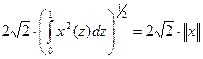 (5)
(5)
(мы воспользовались тем, что  ). Значит,
). Значит,  .
.
Как и в примере 2 пункта б не существует ненулевого вектора, при котором неравенство (5) превращается в равенство (подумайте, почему). Поэтому будем подбирать ненулевые векторы х так, чтобы обе части (5) мало отличались друг от друга. Возьмём последовательность  , состоящую из функций, сосредоточенных в окрестности точки z=1 и таких, что
, состоящую из функций, сосредоточенных в окрестности точки z=1 и таких, что  . Тогда
. Тогда
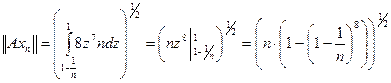 .
.
Значит,  . Перейдем в последнем неравенстве к пределу при
. Перейдем в последнем неравенстве к пределу при  . Воспользовавшись тем, что
. Воспользовавшись тем, что  при
при  , получим:
, получим:
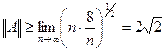 .
.
Из полученных неравенств следует, что  .
.
г) Интегральный оператор, действующий из X в Y.
Пример 1 .
Решение. Из свойства линейности интеграла следует, что А – линейный оператор. Далее,
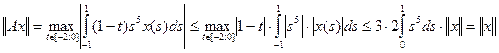 . (6)
. (6)
Значит, оператор А ограничен, причем  . Заметим, что неравенство (6) превращается в равенство при x(t)=sgn(t), но эта функция не принадлежит C[-1;3]. Возьмем следующую последовательность функций из C[-1;3], которые «похожи» на sgn(t) при больших n (сделайте чертеж):
. Заметим, что неравенство (6) превращается в равенство при x(t)=sgn(t), но эта функция не принадлежит C[-1;3]. Возьмем следующую последовательность функций из C[-1;3], которые «похожи» на sgn(t) при больших n (сделайте чертеж):
 .
.
Легко видеть, что  в
в 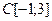 . Вычислим
. Вычислим 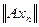 в
в 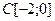 . Так как функция
. Так как функция 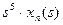 - четная на [-1;1], то
- четная на [-1;1], то

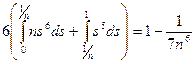 .
.
Значит,  , а потому
, а потому  . Окончательно получаем, что
. Окончательно получаем, что .
.
Задача 3Для последовательности операторов  X,Y
X,Y Norm и
Norm и 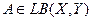
установить: 1) сходится ли 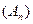 поточечно (сильно) к оператору А; 2) сходится
поточечно (сильно) к оператору А; 2) сходится
ли 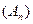 по норме к оператору А.
по норме к оператору А.
Пример 1 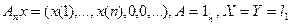
Решение. 1) Заметим, что  .
.
 при
при 
как остаток сходящегося ряда. Значит, последовательность 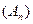 сходится поточечно (т.е. сильно) к оператору А.
сходится поточечно (т.е. сильно) к оператору А.
2) Воспользуемся тем, что 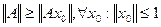 .
.
Возьмем  (единица стоит на
(единица стоит на 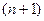 -м месте). Тогда
-м месте). Тогда
 .
.
Так как  , то
, то 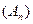 не сходится по норме к А.
не сходится по норме к А.
Задания лабораторной работы
Задача 1Пусть X,Y – нормированные пространства. Выяснить, совпадает ли область
определения 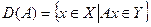 оператора А с нормированным простран-
оператора А с нормированным простран-
ством Х. Является ли оператор А линейным, непрерывным оператором из
D(A) в Y?
| № | Х | Y | A |
| 1.1 | 
| 
| 
|
| 1.2 | 
| 
| 
|
| 1.3 | 
| R | 
|
| 1.4 | 
| 
| 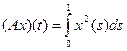
|
| 1.5 | 
| C | 
|
| 1.6 | 
| 
| 
|
Задача 2 Доказать, что оператор А: Х Y является линейным ограниченным, и найти его норму.
Y является линейным ограниченным, и найти его норму.
а) Оператор умножения, действующий из Х в Y.
| № | Х | Y | A |
| 2.1.1 | 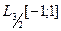
| 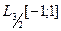
| 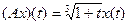
|
| 2.1.2 | 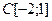
| 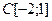
| 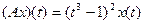
|
| 2.1.3 | 
| 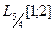
| 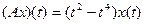
|
| 2.1.4 | 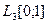
| 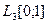
| 
|
| 2.1.5 | 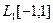
| 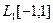
| 
|
| 2.1.6 | 
| 
| 
|
б) Диагональный оператор, действующий из  в
в  .
.
| № | Х | Y | A |
| 2.2.1 | 
| 
|  
|
| 2.2.2 | 
| 
| 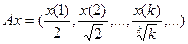
|
| 2.2.3 | 
| 
| 
|
| 2.2.4 | 
| 
| 
|
| 2.2.5 | 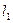
| 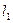
| 
|
| 2.2.6 | 
| 
| 
|
в) Оператор замены переменной.
| № | Х | Y | A |
| 2.3.1 | 
| 
| 
|
| 2.3.2 | 
| 
| 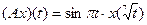
|
| 2.3.3 | 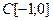
| 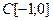
| 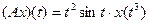
|
| 2.3.4 | 
| 
| 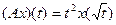
|
| 2.3.5 | 
| 
| 
|
| 2.3.6 | 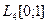
| 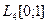
| 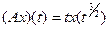
|
г) Интегральный оператор, действующий из X в Y.
| № | Х | Y | A |
| 2.4.1 | 
| 
| 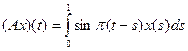
|
| 2.4.2 | 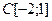
| 
| 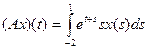
|
| 2.4.3 | 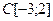
| 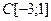
| 
|
| 2.4.4 | 
| 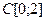
| 
|
| 2.4.5 | 
| 
| 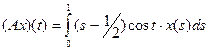
|
| 2.4.6 | 
| 
| 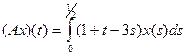
|
Задача 3 Для последовательности операторов  X,Y
X,Y Norm и
Norm и 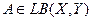
установить: 1) сходится ли 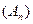 поточечно (сильно) к оператору А; 2) сходится
поточечно (сильно) к оператору А; 2) сходится
ли 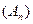 по норме к оператору А.
по норме к оператору А.
| № | Х | Y | A | А |
| 3.1 | 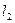
| 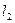
| 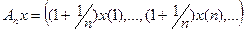
| 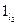
|
| 3.2 | 
| 
| 
| |
| 3.3 | 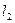
| 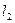
| 
| |
| 3.4 | 
| 
| 
| |
| 3.5 | 
| 
| 
| |
| 3.6 | 
| 
| 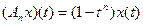
| Ax=x |
Лабораторная работа 9
Обратные операторы
Примеры решения задач
Задача 1 Пусть 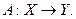 Доказать, что существует непрерывный обратный оператор
Доказать, что существует непрерывный обратный оператор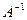 , и построить его.
, и построить его.
Пример 1 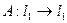 ,
, 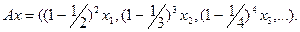
Решение. Очевидно, что А – линейный оператор. Докажем, что А – биекция. Рассмотрим уравнение 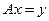 , которое равносильно системе уравнений
, которое равносильно системе уравнений
 ,
,  .
.
Отсюда
 . (1)
. (1)
А так как

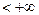 , (2)
, (2)
то 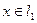 . Мы получили, что
. Мы получили, что  уравнение
уравнение  имеет единственное решение х из
имеет единственное решение х из 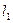 . Значит, А – биекция. Более того, из (1) следует, что обратный оператор
. Значит, А – биекция. Более того, из (1) следует, что обратный оператор 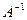 задается формулой
задается формулой

Ограниченность этого оператора следует из оценки (см (2))
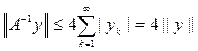 .
.
Пример 2 
Решение. Очевидно, что А – линейный оператор.
Запишем его в виде

и рассмотрим уравнение 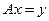 , т. е.
, т. е.
 (3)
(3)
Пусть
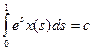 . (4)
. (4)
Тогда (3) примет вид , откуда
, откуда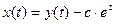 . Мы получили общий вид решения уравнения (3) с неопределенным коэффициентом с. Подставив это в (4), без труда находим, что
. Мы получили общий вид решения уравнения (3) с неопределенным коэффициентом с. Подставив это в (4), без труда находим, что
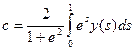 .
.
Таким образом,
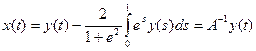 . (5)
. (5)
Итак,  уравнение (2) имеет единственное решение из
уравнение (2) имеет единственное решение из  . Значит, оператор А обратим, причем обратный оператор вычисляется по формуле (5). Непрерывность обратного оператора вытекает из теоремы об оценке интеграла. Действительно, по этой теореме
. Значит, оператор А обратим, причем обратный оператор вычисляется по формуле (5). Непрерывность обратного оператора вытекает из теоремы об оценке интеграла. Действительно, по этой теореме

 ,
,
а потому выполняется неравенство ограниченности  (другое доказательство непрерывности получается из (5) с помощью теоремы о предельном переходе под знаком интеграла Римана).
(другое доказательство непрерывности получается из (5) с помощью теоремы о предельном переходе под знаком интеграла Римана).
Задача 2 Пусть 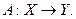
1) Что представляет собой область значений R(A) оператора А?
2) Существует ли на R(A) левый обратный оператор В?
3) Является ли оператор 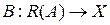 ограниченным, если он существует?
ограниченным, если он существует?
4) Существует ли обратный оператор 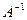 ?
?
Пример 1 .
Решение. 1) Очевидно, что
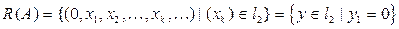
–множество последовательностей из 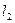 , первая координата которых равна нулю (проверьте). Заметим, что
, первая координата которых равна нулю (проверьте). Заметим, что 
2) Так как уравнение  имеет только нулевое решение, то
имеет только нулевое решение, то  . А это, как известно, равносильно тому, что левый обратный оператор В существует. Легко проверить, что
. А это, как известно, равносильно тому, что левый обратный оператор В существует. Легко проверить, что
 .
.
Действительно, при всех х из 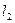 имеем
имеем 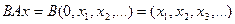 .
.
3) Оператор В ограничен, так как 
4) Поскольку уравнение  не при всех у имеет решение (например, при
не при всех у имеет решение (например, при  ), то А не является сюрьекцией. А это значит, что правого обратного оператора не существует. Следовательно, А необратим.
), то А не является сюрьекцией. А это значит, что правого обратного оператора не существует. Следовательно, А необратим.
Пример 2 .
Решение.  1) По теореме о дифференцировании интеграла с переменным верхним пределом (теорема Барроу) функция
1) По теореме о дифференцировании интеграла с переменным верхним пределом (теорема Барроу) функция  дифференцируема, причем
дифференцируема, причем 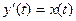 . Значит,
. Значит, 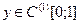 . Кроме того, очевидно, что у(0)=0. Обратно, если
. Кроме того, очевидно, что у(0)=0. Обратно, если 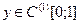 и у(0)=0, то по формуле Ньютона-Лейбница
и у(0)=0, то по формуле Ньютона-Лейбница  . Поэтому
. Поэтому
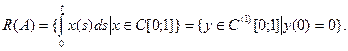
2) Рассмотрим оператор дифференцирования 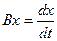 . Поскольку (снова по теореме Барроу)
. Поскольку (снова по теореме Барроу) 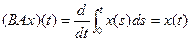 при всех
при всех  , то В – левый обратный для оператора А.
, то В – левый обратный для оператора А.
3) Покажем, что В не является ограниченным оператором. Допустим противное, т.е.
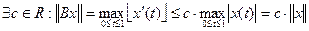 .
.
Возьмём 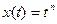
 . Тогда последнее неравенство примет вид
. Тогда последнее неравенство примет вид 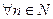
 . Противоречие.
. Противоречие.
4) Поскольку 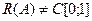 , то А не является сюръекцией. Значит, правого обратного оператора не существует. Следовательно, не существует и
, то А не является сюръекцией. Значит, правого обратного оператора не существует. Следовательно, не существует и 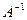 .
.
Задача 3Пусть 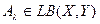 , где
, где  - числовой параметр, Х
- числовой параметр, Х - банахово пространство. Выяснить, при каких
- банахово пространство. Выяснить, при каких  существует обратный оператор к оператору
существует обратный оператор к оператору  , построить его. При каких
, построить его. При каких  оператор
оператор  непрерывно обратим?
непрерывно обратим?
Пример 1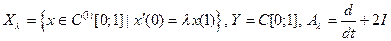 .
.
Решение. Для нахождения обратного оператора рассмотрим в  уравнение
уравнение  x=y, т. е. линейное дифференциальное уравнение
x=y, т. е. линейное дифференциальное уравнение
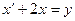 . (6)
. (6)
Нужно выяснить, при каких  у этого уравнения для любого
у этого уравнения для любого  существует единственное решение
существует единственное решение 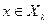 . Другими словами, для любого
. Другими словами, для любого  краевая задача
краевая задача
 (7)
(7)
для уравнения (6) должна иметь единственное непрерывно дифференцируемое решение. Воспользовавшись формулой для общего решения линейного дифференциального уравнения первого порядка, получим общее решение уравнения (1):
 . (8)
. (8)
Требуется узнать, при каких  для любого
для любого  найдется такое С, при котором формула (8) дает решение задачи (7). Подставив (8) в (7), получим после упрощений
найдется такое С, при котором формула (8) дает решение задачи (7). Подставив (8) в (7), получим после упрощений
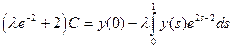 (9)
(9)
Возможны два случая.
а)  . Тогда уравнение (9) имеет единственное решение
. Тогда уравнение (9) имеет единственное решение
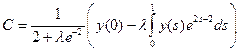
для любого  . Следовательно, при этих
. Следовательно, при этих  существует обратный оператор, который мы найдем, подставив это С в равенство (8):
существует обратный оператор, который мы найдем, подставив это С в равенство (8):
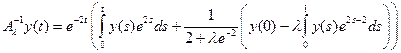 .
.
В силу теоремы Банаха об обратном операторе непрерывность этого оператора будет следовать из непрерывности оператора 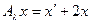 . Последний же факт легко доказать по Гейне. Действительно, если
. Последний же факт легко доказать по Гейне. Действительно, если  в пространстве
в пространстве  , то это значит, что
, то это значит, что  и
и  равномерно на [0;1]. Но тогда и
равномерно на [0;1]. Но тогда и  равномерно на [0;1].
равномерно на [0;1].
б)  . В этом случае уравнение (9) имеет вид
. В этом случае уравнение (9) имеет вид
 .
.
Так как правая часть этого уравнения при некоторых непрерывных у (например, при  не будет равна 0, то при этих у уравнение (9) не имеет решения (относительно С), а потому оператор
не будет равна 0, то при этих у уравнение (9) не имеет решения (относительно С), а потому оператор  не сюръективен.
не сюръективен.
Итак, обратный оператор к оператору  существует тогда и только тогда, когда
существует тогда и только тогда, когда  . Причем при таких
. Причем при таких  оператор
оператор  непрерывно обратим.
непрерывно обратим.
Задания лабораторной работы
Задача 1 Пусть  . Доказать, что существует непрерывный обратный оператор
. Доказать, что существует непрерывный обратный оператор
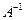 , и построить его.
, и построить его.
| № | X | Y | A |
| 1.1 |
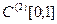
|
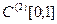
|  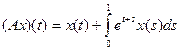
|
| 1.2 |

|

| 
|
| 1.3 |

|

| 
|
| 1.4 |

|

| 
|
| 1.5 | 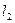
| 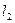
| 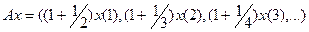
|
| 1.6 | 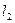
| 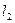
|    
|
Задача 2 Пусть 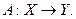
1) Что представляет собой область значений R(A) оператора А?
2) Существует ли на R(A) левый обратный оператор В?
3) Является ли оператор 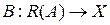 ограниченным, если он существует?
ограниченным, если он существует?
4) Существует ли обратный оператор 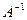 ?
?
| № | X | Y | A |
| 2.1 | 
| 
| 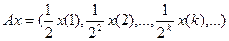
|
| 2.2 | 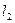
| 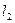
| 
|
| 2.3 | 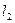
| 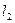
|  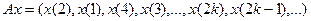
|
| 2.4 | 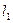
| 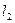
| 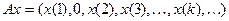
|
| 2.5 | 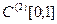
| 
| 
|
| 2.6 | 
| 
| 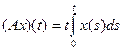
|

Задача 3Пусть 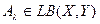 , где
, где  - числовой параметр,
- числовой параметр,  - банахово пространство. Выяснить, при каких
- банахово пространство. Выяснить, при каких  существует обратный оператор к оператору
существует обратный оператор к оператору  , построить его. При каких
, построить его. При каких  оператор
оператор  непрерывно обратим?
непрерывно обратим?
| № | 
| Y | 
|
| 3.1 | 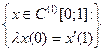
| 
| 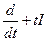
|
| 3.2 | 
| 
| 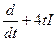
|
| 3.3 | 
| 
|  
|
| 3.4 | 
| 
|  
|
| 3.5 | 
| 
| 
|
| 3.6 | 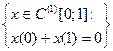
| 
| 
|
ЛИТЕРАТУРА
1 Антоневич, А. Б. Функциональный анализ и интегральные уравнения / А. Б. Антоневич, Я. В. Радыно. − Мн. : БГУ, 2003. − 430 с.
2 Колмогоров, А. Н. Элементы теории функций и функционального анализа / А. Н. Колмогоров, С. В. Фомин. − М. : Наука, 1972. – 496 с.
3 Антоневич, А. Б. Функциональный анализ и интегральные уравнения: Лабораторный практикум / А.Б. Антоневич [и др.]. − Мн. : БГУ, 2003. − 179 с.
4 Кириллов, А. А. Теоремы и задачи функционального анализа / А. А. Кириллов, А. Д. Гвишиани. − М. : Наука, 1979. – 381 с.
Учебное издание
Миротин Адольф Рувимович
Кульбакова Жанна Николаевна
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Лабораторный практикум
Для студентов математического факультета
Специальности 1-31 03 01 Математика
В авторской редакции
Подписано в печать . .09 (141). Формат 60х84 1/16. Бумага писчая № 1.
Гарнитура Таймс. Усл. печ. л. .
Уч.-изд. .л . Тираж 100 экз.
Отпечатано в учреждении образования
«Гомельский государственный университет
имени Франциска Скорины»
246019, г. Гомель, ул. Советская, 104
– Конец работы –
Используемые теги: функциональный, анализ, Интегральные, уравнения0.061
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов