рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Лабораторная работа 4
Реферат Курсовая Конспект
Лабораторная работа 4
Лабораторная работа 4 - раздел Математика, ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ Непрерывные Отображения Примеры Решения Зада...
Непрерывные отображения
Примеры решения задач
Задача 1 Является ли заданное отображение 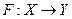 на своей естественной области
на своей естественной области
определения непрерывным в точке x0?
Пример 1  ,
, 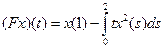 , x0(t) = t.
, x0(t) = t.
Решение. Очевидно, что заданное отображение определено на всем C[0;2]. Представим его в виде: Fx = F1x – F2x, где F1x = x(1), 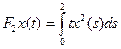 , и покажем, что F1 и F2 непрерывны в любой точке x0
, и покажем, что F1 и F2 непрерывны в любой точке x0  C[0;2]. Пусть последовательность (xn) сходится к x0 в C[0;2]. Тогда
C[0;2]. Пусть последовательность (xn) сходится к x0 в C[0;2]. Тогда
ρL1(F1xn, F1x0)= dt ≤
dt ≤  |xn(t) - x0(t)| = ρc(xn, x0)
|xn(t) - x0(t)| = ρc(xn, x0)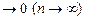 .
.
Отсюда следует, что F1 непрерывно.
Докажем непрерывность F2. Так как функция x0  C[0;2], то она ограничена на [0;2], т. е.
C[0;2], то она ограничена на [0;2], т. е.  M
M  R: |x0(s)| ≤ M
R: |x0(s)| ≤ M  s
s  [0;2]. А так как xn
[0;2]. А так как xn x0 равномерно на [0;2], то, начиная с некоторого номера |xn(s)| ≤ 2M на [0;2] (почему?). Тогда
x0 равномерно на [0;2], то, начиная с некоторого номера |xn(s)| ≤ 2M на [0;2] (почему?). Тогда
ρL1(F2xn, F2x0) =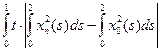 dt =
dt =  =
=
= ≤
≤ 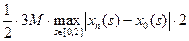 =
=
=3M ρc(xn, x0)
ρc(xn, x0)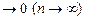 .
.
Отсюда следует, что F2 xn F2 x0 в L1[0;1]. Поэтому в силу произвольности х0 отображение F непрерывно в любой точке из C[0;2].
F2 x0 в L1[0;1]. Поэтому в силу произвольности х0 отображение F непрерывно в любой точке из C[0;2].
Пример 2 F: L2[0;1]  L1[0;1], (Fx)(t) = tx(t3), x0 = 0.
L1[0;1], (Fx)(t) = tx(t3), x0 = 0.
Решение. Пусть последовательность (xn) сходится к x0 в L2[0;1]. Заметим, что
ρL2(xn,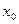 ) =
) =  =
=  .
.
Теперь в силу неравенства Коши-Буняковского
ρL1(Fxn, Fx0)=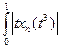 dt =
dt = 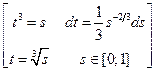 =
=  dt ≤
dt ≤
≤  ρL2(xn,
ρL2(xn,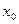 )
)
(аналогичные вычисления показывают, что Fх принадлежит L1[0;1] при х из L2[0;1]; поэтому отображение F определено на всем L1[0;1]). Значит, F – непрерывное отображение в точке 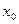 .
.
Пример 3 F: L1[0;1] → L2[0;1], (Fx)(t) = 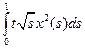 , x0 = 0.
, x0 = 0.
Решение. Покажем, что отображение не является непрерывным. Возьмём последовательность xn = 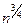 .
. 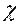 [0;1/n], которая
[0;1/n], которая  0 в L1[0;1] (действительно,
0 в L1[0;1] (действительно,
ρL1(xn,0)=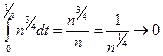 при
при 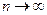 ).
).
Рассмотрим теперь выражение
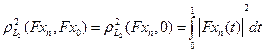 =
= = =
= = ==
==  =
=  =
=  .
.
Следовательно, последовательность ρL2(Fxn, Fx0) не стремится к нулю при 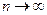 , а потому Fxn не стремится к Fx0.
, а потому Fxn не стремится к Fx0.
Пример 4 F: L2[0;1] → L1[0;1], (Fx)(t) =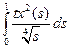 , x0 = 0.
, x0 = 0.
Решение. Покажем, что отображение не является непрерывным. Заметим, что
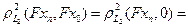
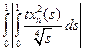 dt =
dt = 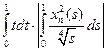 =
= 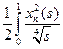 ds.
ds.
Возьмем последовательность xn =  .
. 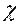 [0;1/ n-2], которая → 0 в L2[0;1], так как
[0;1/ n-2], которая → 0 в L2[0;1], так как 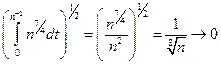 при n → ∞.
при n → ∞.
Тогда
ρL1(Fxn,0) =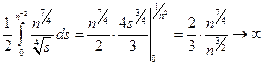 при n→ ∞,
при n→ ∞,
а потому Fxn не стремится к Fx0.
Задача 2 Является ли заданное отображение 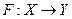 : а) непрерывным; б) равномерно
: а) непрерывным; б) равномерно
непрерывным; в) удовлетворяющим условию Липшица?
Пример 1 X = Y = C[-4;2], (Fx)(t) = x(t)sin x(t).
Решение. а) Отображение F является непрерывным, так как
ρ(Fx,Fx0) = 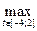 |x(t)sin x(t) - x0(t)sin x0(t)| ≤
|x(t)sin x(t) - x0(t)sin x0(t)| ≤ 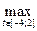 |x(t)sin x(t) - x0(t)sin x(t)| +
|x(t)sin x(t) - x0(t)sin x(t)| +
+ |x0(t)sin x(t) - x0(t)sin x0(t)| ≤ 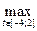 |x(t) - x0(t)| +
|x(t) - x0(t)| +
+ 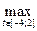 |x0(t)
|x0(t) 2sin
2sin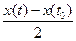 ·cos
·cos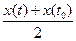 )| ≤
)| ≤ 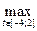 |x(t) - x0(t)| + M
|x(t) - x0(t)| + M
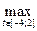 |x(t) - x0(t)| =
|x(t) - x0(t)| =
= (M+1)ρ(x,x0)
(здесь M =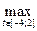 | x0(t) |; мы воспользовались неравенством
| x0(t) |; мы воспользовались неравенством 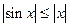 ).
).
б) Покажем, что F не является равномерно непрерывным. Возьмём
xn(t) = 2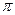
 , yn(t)=
, yn(t)=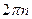 . Тогда ρ(xn,yn)=
. Тогда ρ(xn,yn)=  → 0 при n→ ∞, но
→ 0 при n→ ∞, но
ρ(Fxn, Fyn)= 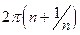 sin
sin -
- 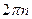
 sin
sin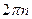 =
= 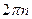 sin
sin +
+ sin
sin = =
= = ,
,
а значит, ρ(Fxn, Fyn) не стремится к нулю при n→ ∞. Это противоречит определению равномерной непрерывности (проверьте).
в) Так как F не является равномерно непрерывным, то оно не удовлетворяет условию Липшица (почему?).
Пример 2 X = l2, Y = l∞ , Fx =  .
.
Решение. Покажем, что F удовлетворяет условию Липшица с константой L=1. Заметим, что
ρl∞(Fx, Fy) =  {
{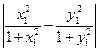 ; | x1 - y1 |; | x1 - y1 |; …}.
; | x1 - y1 |; | x1 - y1 |; …}.
Обозначим f(x) =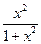 . Тогда
. Тогда
|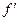 (x)| =
(x)| = =
= .
.
Следовательно, по теореме Лагранжа | f(x1) - f(y1) | ≤ | x1 - y1 |, а значит,
ρl∞(Fx, Fy) =  {
{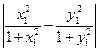 ; | x1 - y1 |; | x1 - y1 |; …} ≤
; | x1 - y1 |; | x1 - y1 |; …} ≤  | xk - yk | ≤ ρl2(x,y).
| xk - yk | ≤ ρl2(x,y).
Так как F удовлетворяет условию Липшица, то оно равномерно непрерывно, а потому и непрерывно.
Пример 3 X = L1[0;1], Y = L2[-1;1], (Fx)(t)=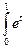 arctgx(s)ds.
arctgx(s)ds.
Решение. Покажем, что F удовлетворяет условию Липшица. Действительно,
ρL2(Fx, Fy) = =
=  =
=
= 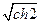
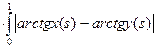 ds.
ds.
Так как 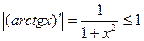 , то по теореме Лагранжа
, то по теореме Лагранжа  . Поэтому при любых х,у
. Поэтому при любых х,у
ρL2(Fx, Fy) 
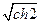 ρL1(x,y).
ρL1(x,y).
Так как F удовлетворяет условию Липшица, то оно является равномерно непрерывным.
Пример 4 X=l2 Y=l1 , Fx= .
.
Решение. а) Покажем, что F непрерывно. Действительно, если xn → x0 в l2, то чис-ловая последовательность xn(21) сходится к x0(21). Тогда
ρl2(Fxn, Fx0) = 0 при n→ ∞.
0 при n→ ∞.
б) Покажем, что F не является равномерно непрерывным. Пусть
xn(21) =  , yn(21) = n, xn (k) = yn (k) = 0
, yn(21) = n, xn (k) = yn (k) = 0 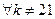 .
.
Тогда
ρl2(xn,yn) = при n→ ∞,
при n→ ∞,
но
ρl1(Fxn,Fyn) =  при n→ ∞.
при n→ ∞.
в) Так как F не является равномерно непрерывным, то оно не удовлетворяет и условию Липшица.
Задания лабораторной работы
Задача 1 Выяснить, является ли заданное отображение 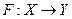 на своей естественной
на своей естественной
области определения непрерывным в точке x0?
| № | X | Y | F | x0(t) |
| 1.1 | L2[0;1] | L1[0;1] | (Fx)(t) = 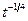 sin x(t) sin x(t)
| t2 |
| 1.2 | C[0;1] | L1[0;1] | (Fx)(t) =sin x2(t) | t |
| 1.3 | L2[0;1] | L2[0;1] | (Fx)(t) = x(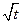 ) )
| 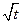
|
| 1.4 | C[0;1] | C[0;1] |
(Fx)(t) = ∫t|x(s)|/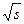 ds
0 ds
0
| t |
| 1.5 | C[0;1] | C[0;2] | (Fx)(t) = 2x3(t/2) | |
| 1.6 | L1[0;1] | L2[0;1] | (Fx)(t) = x(t) |
Задача 2 Является ли заданное отображение 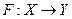 : а) непрерывным; б) равномерно
: а) непрерывным; б) равномерно
непрерывным; в) удовлетворяющим условию Липшица?
| № | X | Y | F |
| 2.1 | C[0;1] | C[0;1] | (Fx)(t) =x2(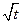 )et )et
|
| 2.2 | C[-1;1] | C[-1;1] | (Fx)(t) =x(t)/(1+x2(t)) |
| 2.3 | L2[-1;0] | L1[-1;0] | (Fx)(t) =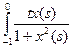 ds ds
|
| 2.4 | C[-1;2] | L1[-1;2] | (Fx)(t) =
|
| 2.5 | l1 | l1 | Fx = (cosx (1), x (2), x (3),…, x(k),…) |
| 2.6 | C[-5;2] | L1[-5;2] | Fx(t) =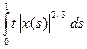
|
– Конец работы –
Эта тема принадлежит разделу:
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Учреждение образования... Гомельский государственный университет... имени Франциска Скорины...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Лабораторная работа 4
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов