рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Эксцентриситет вершины. Релейно-контактные (переключательные) схемы. Алгебра высказываний. Операции над множествами. Графы и Способы задания графов. Релейно-контактные схемы
Реферат Курсовая Конспект
Эксцентриситет вершины. Релейно-контактные (переключательные) схемы. Алгебра высказываний. Операции над множествами. Графы и Способы задания графов. Релейно-контактные схемы
Эксцентриситет вершины. Релейно-контактные (переключательные) схемы. Алгебра высказываний. Операции над множествами. Графы и Способы задания графов. Релейно-контактные схемы - раздел Математика, ...

также однозначно определяет структуру графа.
Весьма важным видом графа является связный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путем.
Рассмотрим связный граф  , пусть
, пусть  и
и 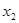 - две его вершины. Длина кратчайшего
- две его вершины. Длина кратчайшего  - маршрута называется расстоянием между вершинами
- маршрута называется расстоянием между вершинами  и
и 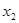 обозначается через
обозначается через  . Очевидно, что расстояние между вершинами является простой цепью и
. Очевидно, что расстояние между вершинами является простой цепью и  . Для любой вершины
. Для любой вершины  величина
величина
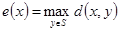 (1.13.6)
(1.13.6)
называется эксцентриситетом вершины  . Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается
. Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается 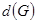 , т. е.
, т. е.
 . (1.13.7)
. (1.13.7)
Минимальный из эксцентриситетов вершин графа называется его радиусом и обозначается через  :
: 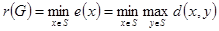 . (1.13.8)
. (1.13.8)
Вершина  называется периферийной, если ее эксцентриситет равен диаметру графа, т. е.
называется периферийной, если ее эксцентриситет равен диаметру графа, т. е. 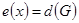 . Простая цепь, расстояние между концами которой равно
. Простая цепь, расстояние между концами которой равно 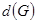 , называется диаметральной цепью.
, называется диаметральной цепью.
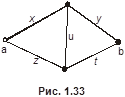
 Вершина
Вершина  называется центральной, если
называется центральной, если  . Множество всех центральных вершин графа называется его центром. Центром может быть единственная вершина графа или несколько вершин (см. рис. 1.15). Здесь
. Множество всех центральных вершин графа называется его центром. Центром может быть единственная вершина графа или несколько вершин (см. рис. 1.15). Здесь 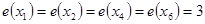 ,
, 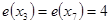 ,
,
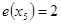 . Таким образом,
. Таким образом,  . Периферийные вершины
. Периферийные вершины 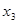 и
и  , диаметральные цепи:
, диаметральные цепи: 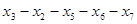 и
и 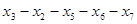 , центральная вершина
, центральная вершина  .
.
1.13.4. Релейно-контактные (переключательные) схемы. Рассмотрим еще один способ реализации функций алгебры логики – релейно-контактные схемы (РКС), широко используемые в электронно-вычислительной технике. Описание и конструирование таких схем в силу их громоздкости весьма затруднительно. Однако оказалось, что при конструировании РКС можно использовать аппарат булевых функций.
Исходное замечание состоит в том, что если логической переменной  поставить в соответствие проводник, по которому ток идет или нет в зависимости от того
поставить в соответствие проводник, по которому ток идет или нет в зависимости от того 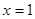 или
или 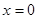 , то последовательному соединению проводников отвечает конъюнкция переменных, а параллельному – дизъюнкция. Часто проводники на схемах заменяют обозначением специальных устройств – переключателей, которые могут быть механическими и электронными. Многократно используя параллельно-последовательные соединения, можно строить сложные схемы. Мы ограничимся только схемами, в которых соединяются лишь контакты. Контакт или переключатель будем изображать отрезком или прямоугольником, концы контакта называть полюсами. Конструкция, изображенная на рис. 1.16, называется двухполюсником. Двухполюсник будем снабжать символом переменной
, то последовательному соединению проводников отвечает конъюнкция переменных, а параллельному – дизъюнкция. Часто проводники на схемах заменяют обозначением специальных устройств – переключателей, которые могут быть механическими и электронными. Многократно используя параллельно-последовательные соединения, можно строить сложные схемы. Мы ограничимся только схемами, в которых соединяются лишь контакты. Контакт или переключатель будем изображать отрезком или прямоугольником, концы контакта называть полюсами. Конструкция, изображенная на рис. 1.16, называется двухполюсником. Двухполюсник будем снабжать символом переменной  , если контакт замыкающий, и
, если контакт замыкающий, и 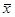 , если размыкающий. Двухполюсники соединяются полюсами. В результате схема будет представлять из себя граф.
, если размыкающий. Двухполюсники соединяются полюсами. В результате схема будет представлять из себя граф.
 Граф
Граф 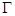 с
с 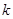 полюсами, в котором каждое ребро помечено буквой из алфавита
полюсами, в котором каждое ребро помечено буквой из алфавита  , называется
, называется 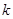 -полюсной контактной схемой, реализующей булевы функции переменных
-полюсной контактной схемой, реализующей булевы функции переменных  , или
, или  -схемой. Контактная схема называется связной (сильно связной, паралллельно-последовательной), если таковым является ее граф. Параллельно-последовательная схема называется
-схемой. Контактная схема называется связной (сильно связной, паралллельно-последовательной), если таковым является ее граф. Параллельно-последовательная схема называется 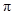 -схемой. В графе выделяются две вершины: вход и выход. Часто вход изображает полюс в виде светлого кружка, остальные полюса изображаются темными кружками.
-схемой. В графе выделяются две вершины: вход и выход. Часто вход изображает полюс в виде светлого кружка, остальные полюса изображаются темными кружками.
Какую же функцию алгебры логики реализует контактная схема? Эта функция равна единице при тех значениях аргументов, при которых в схеме есть проводимость, и нулю, если проводимости нет. Пусть 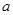 и
и 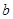 - два полюса контактной схемы
- два полюса контактной схемы  ,
,  - некоторая цепь, соединяющая
- некоторая цепь, соединяющая 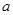 и
и 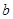 , и
, и  - конъюнкция букв, приписанных ребрам цепи
- конъюнкция букв, приписанных ребрам цепи  . Функция
. Функция 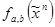 , определяемая формулой
, определяемая формулой
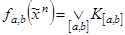 , (1.13.9)
, (1.13.9)
в которой дизъюнкция берется по всем простым цепям схемы, соединяющим полюса 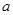 и
и 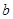 , называется функцией проводимости между полюсами
, называется функцией проводимости между полюсами 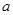 и
и 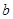 схемы
схемы 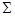 . На самом деле для получения функции проводимости достаточно брать дизъюнкцию не по всем цепям, а лишь по некоторым.
. На самом деле для получения функции проводимости достаточно брать дизъюнкцию не по всем цепям, а лишь по некоторым.
Цепь  называется существенной, если она ни через какую вершину графа не проходит дважды. Оказывается, что дизъюнкция конъюнкций, соответствующих существенным цепям, равносильна функции проводимости. Действительно, пусть имеется некоторая цепь, в которой некоторая вершина встречается дважды. Отбросим все контакты, которые встречаются между двумя прохождениями через эту вершину. Ясно, что при этом мы вновь получим цепь, причем если все контакты исходной цепи были замкнуты, то будут замкнуты и все контакты вновь полученной цепи. Таким образом, последовательно сокращая цепь, можно получить существенную цепь, в которой будет проводимость, если была проводимость в исходной цепи.
называется существенной, если она ни через какую вершину графа не проходит дважды. Оказывается, что дизъюнкция конъюнкций, соответствующих существенным цепям, равносильна функции проводимости. Действительно, пусть имеется некоторая цепь, в которой некоторая вершина встречается дважды. Отбросим все контакты, которые встречаются между двумя прохождениями через эту вершину. Ясно, что при этом мы вновь получим цепь, причем если все контакты исходной цепи были замкнуты, то будут замкнуты и все контакты вновь полученной цепи. Таким образом, последовательно сокращая цепь, можно получить существенную цепь, в которой будет проводимость, если была проводимость в исходной цепи.
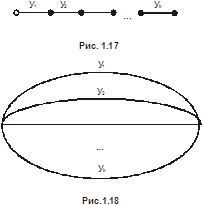 Посмотрим теперь как обстоит дело с обратной задачей: построением по функции реализующей ее схемы. Представим функцию в виде ДНФ. Каждой входящей в ДНФ элементарной конъюнкции
Посмотрим теперь как обстоит дело с обратной задачей: построением по функции реализующей ее схемы. Представим функцию в виде ДНФ. Каждой входящей в ДНФ элементарной конъюнкции 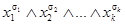 поставим в соответствие схему (рис. 1.17), состоящую из последовательно соединенных контактов
поставим в соответствие схему (рис. 1.17), состоящую из последовательно соединенных контактов 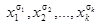 . Это схема элементарной конъюнкции. На рис. 1.17 и 1.18 величины
. Это схема элементарной конъюнкции. На рис. 1.17 и 1.18 величины 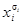 обозначены через
обозначены через 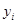 . После отождествления между собой, с одной стороны, входов всех этих схем, с другой стороны – выходов, получим функцию, соответствующую заданной схеме. Естественно, можно реализовать функцию по схемам также исходя из КНФ. Каждой элементарной дизъюнкции
. После отождествления между собой, с одной стороны, входов всех этих схем, с другой стороны – выходов, получим функцию, соответствующую заданной схеме. Естественно, можно реализовать функцию по схемам также исходя из КНФ. Каждой элементарной дизъюнкции 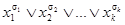 поставим в соответствие схему, изображенную на рис. 1.18. Затем последовательно соединим все эти схемы для всех элементарных дизъюнкций, входящих в КНФ, так, чтобы вход последующей схемы совпадал с выходом предыдущей.
поставим в соответствие схему, изображенную на рис. 1.18. Затем последовательно соединим все эти схемы для всех элементарных дизъюнкций, входящих в КНФ, так, чтобы вход последующей схемы совпадал с выходом предыдущей.
Схему, состоящую из одного контакта, называют элементарной. Ясно, что любая 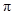 -схема может быть получена из элементарных за некоторое число шагов при помощи параллельных и последовательных соединений. Каждому способу построения
-схема может быть получена из элементарных за некоторое число шагов при помощи параллельных и последовательных соединений. Каждому способу построения  -схемы из элементарных схем отвечает представление функции проводимости в виде формулы, содержащей только дизъюнкции, конъюнкции и отрицания.
-схемы из элементарных схем отвечает представление функции проводимости в виде формулы, содержащей только дизъюнкции, конъюнкции и отрицания.
 Если контактная схема является
Если контактная схема является 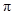 -схемой, то ее можно разбить на несколько схем, соединенных либо последовательно, либо параллельно. Обратное тоже верно. Если схема не допускает разбиения на две схемы, соединенные либо последовательно, либо параллельно, она не является
-схемой, то ее можно разбить на несколько схем, соединенных либо последовательно, либо параллельно. Обратное тоже верно. Если схема не допускает разбиения на две схемы, соединенные либо последовательно, либо параллельно, она не является 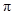 -схемой. Для примера рассмотрим схему “мостик” (рис. 1.19), которая не является элементарной. Если две схемы соединены последовательно, то у полученной общей схемы все полюсы, кроме соединяющего, либо не имеют общих контактов ни с входом, ни с выходом всей схемы, либо имеют общий контакт или только с входом, или только с выходом. Очевидно, что какой бы из внутренних полюсов на рис. 1.19 мы не приняли за соединяющий подсхемы, оставшийся полюс будет иметь общий контакт как с входом, так и с выходом схемы. Поэтому схему “мостик” нельзя получить последовательным соединением двух схем.
-схемой. Для примера рассмотрим схему “мостик” (рис. 1.19), которая не является элементарной. Если две схемы соединены последовательно, то у полученной общей схемы все полюсы, кроме соединяющего, либо не имеют общих контактов ни с входом, ни с выходом всей схемы, либо имеют общий контакт или только с входом, или только с выходом. Очевидно, что какой бы из внутренних полюсов на рис. 1.19 мы не приняли за соединяющий подсхемы, оставшийся полюс будет иметь общий контакт как с входом, так и с выходом схемы. Поэтому схему “мостик” нельзя получить последовательным соединением двух схем.
 Если общая схема – результат параллельного соединения двух схем, то ее контакты и полюсы можно разбить на две части так, чтобы либо в одной части содержались контакты, непосредственно соединяющие вход и выход, либо полюсы, входящие в рассматриваемые различные две части схемы и отличные от входа и выхода, не будут иметь общих контактов. Ни первая, ни вторая возможность на схеме рис. 1.19 не может реализоваться. Следовательно, эта схема не является
Если общая схема – результат параллельного соединения двух схем, то ее контакты и полюсы можно разбить на две части так, чтобы либо в одной части содержались контакты, непосредственно соединяющие вход и выход, либо полюсы, входящие в рассматриваемые различные две части схемы и отличные от входа и выхода, не будут иметь общих контактов. Ни первая, ни вторая возможность на схеме рис. 1.19 не может реализоваться. Следовательно, эта схема не является 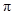 -схемой.
-схемой.
Две контактные схемы называются эквивалентными, если они реализуют одну и ту же булеву функцию или одну и ту же систему функций. Схема называется минимальной, если она содержит наименьшее возможное число контактов среди всех схем, имеющих ту же функцию проводимости.
Пример 3. Найти функции, реализуемые схемами на рис. 1.20.
Первые две функции представлены 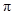 -схемами, поэтому их восстановление довольно просто: а)
-схемами, поэтому их восстановление довольно просто: а) 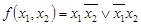 ; б)
; б)  .
.
Для последнего пункта (в) составим по формуле (1.12.9) функцию проводимости. Для этого необходимо перечислить все цепи, соединяющие начальный 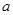 и конечный
и конечный 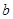 полюсы схемы:
полюсы схемы: 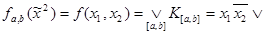
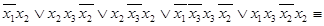
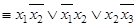 .
.
Практическое занятие № 2. Математические основы информатики.
Алгебра высказываний. Операции над множествами. Графы и
Способы задания графов. Релейно-контактные схемы
Основное понятие алгебры логики – высказывание. Основные понятия любой отрасли науки не могут быть определены строго формально, а лишь поясняются. Логическое значение высказывания “истина” (“ложь”) чаще всего обозначаются цифрой 1 (0). Все высказывания можно разделить на простые и составные или сложные. Логическое значение любого высказывания легко может быть установлено с помощью таблиц истинности основных логических операций.
Пример 1. Определить являются ли высказываниями следующие предложения, и установить истинность или ложность имеющихся высказываний:
1. число 15 не делится на 3;
2. летайте самолётами Аэрофлота!
3. есть ли жизнь на Марсе?
4. в Петербурге более 4-х миллионов жителей;
5. все действительные числа удовлетворяют коммутативному закону.
Из приведённых пяти предложений второе и третье не являются высказываниями, т. к. высказыванием может быть лишь повествовательное предложение. Первое высказывание ложно, четвертое и пятое – истинны.
Пример 2. Составить таблицу истинности для формулы  .
.
Применение таблицы истинности – самый простой способ исследования булевой функции. Каждая таблица для функции  переменных содержит
переменных содержит  строк, поэтому таблицы истинности удобно применять, если функция содержит не более 3-4-х переменных. В нашем случае
строк, поэтому таблицы истинности удобно применять, если функция содержит не более 3-4-х переменных. В нашем случае
Таблица 1.19

| 
| 
| 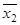
| 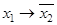
| 
| 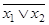
| 
| 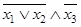
| 
|
По табл. 1.19 видно, что формула  - выполнима, т. к. принимает значения 0 и 1 при разных наборах переменных
- выполнима, т. к. принимает значения 0 и 1 при разных наборах переменных 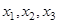 .
.
Пример 3. Доказать, что если формулы  и
и 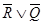 тождественно истинны, то формула
тождественно истинны, то формула 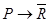 также тождественно истинна.
также тождественно истинна.
Предположим обратное, пусть 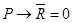 . Тогда из таблицы 1.16
. Тогда из таблицы 1.16  , т. е.
, т. е.  . Следовательно,
. Следовательно,  и
и 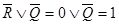 , т. е.
, т. е.  и
и  одновременно, что невозможно. Таким образом, наше предположение неверно и
одновременно, что невозможно. Таким образом, наше предположение неверно и 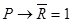 .
.
Пример 4. Булевы функции, представленные по формулам (1.13.4) и (1.13.5), находятся в виде совершенных дизъюнктивной и конъюнктивной нормальных форм. К такому виду любую булеву функцию можно привести путём эквивалентных преобразований с использованием формул (1.13.1)-(1.13.3). Однако самый простой, но не самый удобный способ – использование таблицы истинности.
По структуре формулы (1.13.4) ясно, что в её правой части стоят логические слагаемые, каждое из которых состоит из логического произведения всех переменных исходной формулы или их отрицаний, причём только из тех строк таблицы истинности, в которых сама функция равна единице.
Поэтому, чтобы получить совершенную дизъюнктивную нормальную форму булевой функции 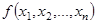 , необходимо записать в виде дизъюнкции все выражения вида
, необходимо записать в виде дизъюнкции все выражения вида  только в тех строках таблицы истинности, где
только в тех строках таблицы истинности, где 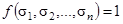 .
.
Рассмотрим в качестве примера функцию  и её таблицу истинности 1.20.
и её таблицу истинности 1.20.
Тогда 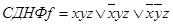 . Форму (1.13.5) удобнее получать не напрямую, а по формуле
. Форму (1.13.5) удобнее получать не напрямую, а по формуле  . В нашем случае
. В нашем случае  и
и 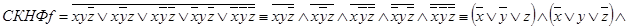
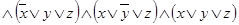 .
.
Таблица 1.20

| 
| 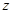
| 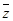
| 
| 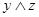
| 
| 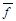
|
Алгебра логики и теория множеств являются двумя интерпретациями (моделями) одной общей теории, называемой алгеброй Буля*. Поэтому все понятия алгебры логики и теории множеств очень похожи.
 Пример 5. Доказать равенство
Пример 5. Доказать равенство 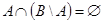 . Проще всего это сделать с помощью диаграмм Эйлера – Венна (см. рис. 1.21). Видно, что множества
. Проще всего это сделать с помощью диаграмм Эйлера – Венна (см. рис. 1.21). Видно, что множества  и
и 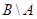 непересекающиеся, т. е. не имеют общих элементов. То же самое можно полу-чить чисто формально:
непересекающиеся, т. е. не имеют общих элементов. То же самое можно полу-чить чисто формально: 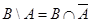 (см. рис. 1.21),
(см. рис. 1.21), 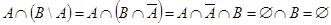 .
.
Пример 6. Пусть  ,
, 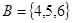 . Найти
. Найти  ,
, 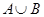 ,
,  ,
,  ,
, 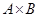 ,
,  .
.
 ,
, 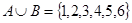 ,
, 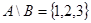 ,
,  ,
, 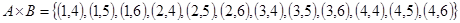 ,
, 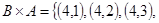
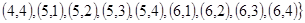 , очевидно
, очевидно 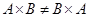 .
.
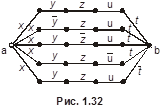
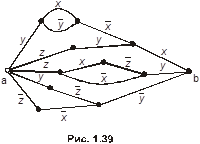
Пример 7. Дано бинарное отношение  , изображённое на рис. 1. 22. Определить является ли оно рефлексивным, иррефлексивным, симметричным, антисимметричным, транзитивным?
, изображённое на рис. 1. 22. Определить является ли оно рефлексивным, иррефлексивным, симметричным, антисимметричным, транзитивным?
 Матрица этого отношения имеет вид
Матрица этого отношения имеет вид 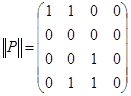 . Отношение
. Отношение  не рефлексивно, т. к. на главной диагонали его матрицы имеется два нуля; это отношение не иррефлексивно, т. к.
не рефлексивно, т. к. на главной диагонали его матрицы имеется два нуля; это отношение не иррефлексивно, т. к.  . Матрица
. Матрица  не симметрична, тогда не симметрично и отношение
не симметрична, тогда не симметрично и отношение 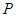 ; для симметричных отношений справедливо
; для симметричных отношений справедливо 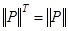 , что, очевидно, не выполняется в данном случае.
, что, очевидно, не выполняется в данном случае. 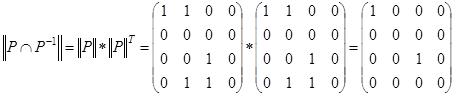 . Отношение
. Отношение 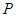 антисимметрично, т. к. все элементы, стоящие вне главной диагонали матрицы
антисимметрично, т. к. все элементы, стоящие вне главной диагонали матрицы 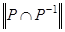 , равны нулю.
, равны нулю.
Транзитивность проще проверить по определению, используя элементы этого отношения: 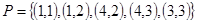 . По определению отношение
. По определению отношение 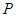 транзитивно, если из
транзитивно, если из 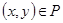 и
и  следует, что
следует, что 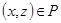 . В нашем случае
. В нашем случае  ,
,  , но и
, но и  ;
; 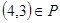 ,
, 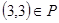 , но и
, но и 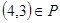 , т. е.
, т. е. 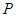 транзитивно.
транзитивно.
Пример 8. Для графов, изображённых на рис. 1.23, составить матрицу смежности вершин и инциденций.
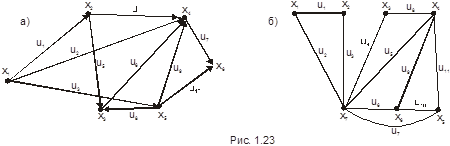
а) Дан ориентированный граф. Тогда

и
б) Этот граф неориентированный, поэтому матрица смежности вершин будет симметрической, а матрица инциденций – бинарной.


Пример 9. По данной матрице смежности вершин 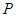 и инциденций
и инциденций 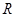 нарисовать соответствующий граф.
нарисовать соответствующий граф.
 ,
,  .
.
 По первой матрице
По первой матрице 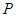 может быть построен ориентированный мульти- и псевдограф, изображённый на рис. 1.24. Следует помнить, что рисунок графа может быть и иным по расположению вершин и форме дуг, важно лишь количество вершин и дуг и порядок их инцидентности. Так как матрица
может быть построен ориентированный мульти- и псевдограф, изображённый на рис. 1.24. Следует помнить, что рисунок графа может быть и иным по расположению вершин и форме дуг, важно лишь количество вершин и дуг и порядок их инцидентности. Так как матрица  бинарна, то ей соответствующий граф будет неориентированным. Он изображён на рис. 1.25.
бинарна, то ей соответствующий граф будет неориентированным. Он изображён на рис. 1.25.
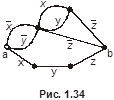
Пример 10. Найти эксцентриситет вершин, радиус и диаметр графа, изображённого на рис. 1.25.
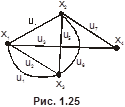
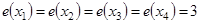 ,
, 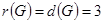 . Все вершины центральные и периферийные. Диаметральные цепи:
. Все вершины центральные и периферийные. Диаметральные цепи:
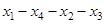 ,
, 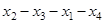 ,
, 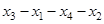 ,
,
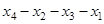 ,
, 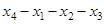 и т. п.
и т. п.
Пример 11. Реализовать релейно-контактными схемами функции: а) 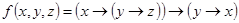 ;
;
б)  .
.
Поскольку релейно-контактные схемы реализуются на основе элементарных конъюнкции и дизъюнкции, то при необходимости следует упростить формулу по правилам (1.13.1)-(1.13.3).
а) 
 . Тогда релейно-контактная схема имеет вид, изображённый на рис. 1.26 а).
. Тогда релейно-контактная схема имеет вид, изображённый на рис. 1.26 а).


б) В этом случае формулу упрощать не требуется. Релейно-контактная схема этой формулы изображена на рис. 1.26 б).
Пример 12. Найти функции, реализуемые релейно-контактными схемами, изображёнными на рис. 1.27.
а)  ;
;
б) 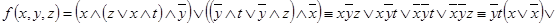
 .
.
1.14.1. Обозначить элементарные высказывания буквами и записать следующие высказывания с помощью символов алгебры логики:
а)  или
или  ;
;
б) если число 512 делится на 2 и 8, то оно делится на 16;
в) тает лёд и  .
.
1.14.2. Пусть высказывание 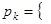 мишень поражена
мишень поражена 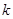 -м выстрелом
-м выстрелом ,
, 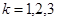 . Что означают следующие высказывания:
. Что означают следующие высказывания:
а) 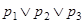 ;
;
б) 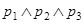 ;
;
в) 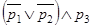 ?
?
1.14.3. Составить таблицы истинности для формул:
а)  ;
;
б) 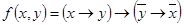 ;
;
в)  .
.
1.14.4. По таблице истинности получить СДНФ и СКНФ для формул:
а) 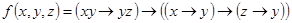 ;
;
б) 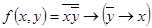 ;
;
в) 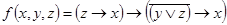 .
.
1.14.5. Доказать следующие тождества:
а)  ;
;
б) 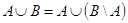 ;
;
в) 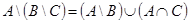 .
.
1.14.6. Определить в каком отношении (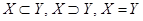 ) находятся множества
) находятся множества 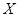 и
и 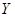 , если:
, если:
а)  ;
;
б)  ;
;
в) 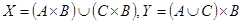 .
.
1.14.7. По данной матрице смежности вершин 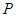 или инциденций
или инциденций 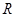 построить соответствующий граф:
построить соответствующий граф:
а)  ; б)
; б) 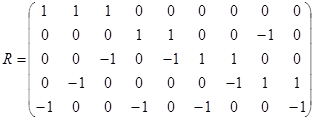 ;
;
в)  ; г)
; г)  .
.
1.14.8. Для графов, изображённых на рис. 1.28, составить матрицы смежности вершин и инциденций:

1.14.9. Построить 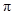 -схемы для формул:
-схемы для формул:
а) 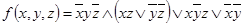 ;
;
б) 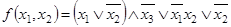 ;
;
в)  .
.
1.14.10. Найти функции, реализуемые контактными схемами, изображёнными на рис. 1.29.

1.14.11. Варианты расчётно-графической работы.
Задание к расчётно-графической работе.
1. По таблице истинности найти СДНФ формулы алгебры логики.
2. Доказать равенство.
3. По данной матрице смежности вершин 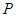 или инциденций
или инциденций 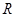 построить граф и найти его метрические характеристики (эксцентриситеты вершин, радиус и диаметр графа).
построить граф и найти его метрические характеристики (эксцентриситеты вершин, радиус и диаметр графа).
4. Восстановить булеву функцию по данной релейно-контактной схеме ( см. рис. 1.30-1.44) или построить релейно-контактную схему по данной функции.
Вариант 1
1.  ;
;
2. 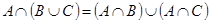 ;
;
3. 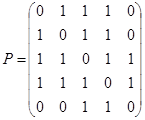 ;
;
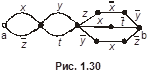
4.
Вариант 2
1.  ;
;
2.  ;
;
3.  ;
;
4. 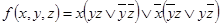 .
.
Вариант 3
1. 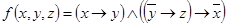 ;
;
2. 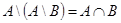 ;
;
3.  ;
;
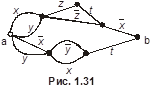
4.
Вариант 4
1.  ;
;
2.  ;
;
3.  ;
;
4.  .
.
Вариант 5
1.  ;
;
2. 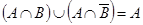 ;
;
3.  ;
;
4.
Вариант 6
1.  ;
;
2.  ;
;
3. 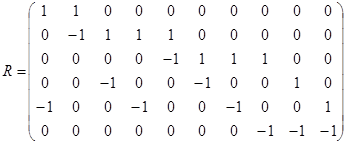 ;
;
4.  .
.
Вариант 7
1. 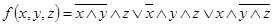 ;
;
2. 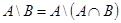 ;
;
3. 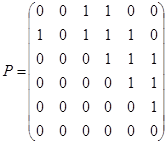 ;
;
4.
Вариант 8
1. 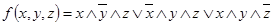 ;
;
2. 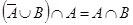 ;
;
3.  ;
;
4. 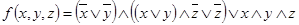 .
.
Вариант 9
1.  ;
;
2. 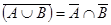 ;
;
3. 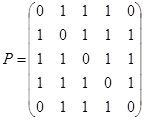 ;
;
4.
Вариант 10
1. 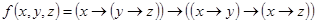 ;
;
2. 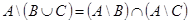 ;
;
3.  ;
;
4.  .
.
Вариант 11
1. 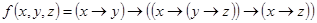 ;
;
2. 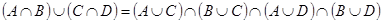 ;
;
3.  ;
;
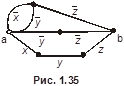
4.
Вариант 12
1.  ;
;
2. 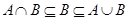 ;
;
3. 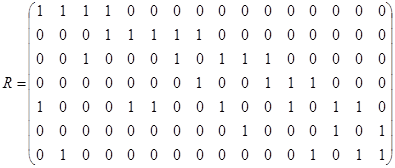 ;
;
4. 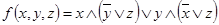 .
.
Вариант 13
1.  ;
;
2.  ;
;
3.  ;
;

4.
Вариант 14
1. 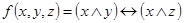 ;
;
2.  ;
;
3. 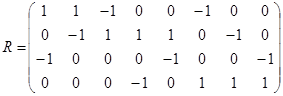 ;
;
4.  .
.
Вариант 15
1. 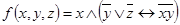 ;
;
2.  ;
;
3.  ;
;

4.
Вариант 16
1. 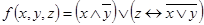 ;
;
2.  ;
;
3. 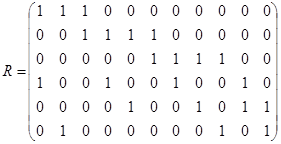 ;
;
4.  .
.
Вариант 17
1. 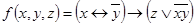 ;
;
2.  ;
;
3. 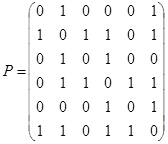 ;
;

4.
Вариант 18
1. 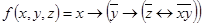 ;
;
2.  ;
;
3. 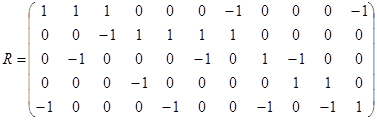 ;
;
4. 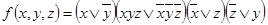 .
.
Вариант 19
1. 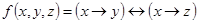 ;
;
2.  ;
;
3. 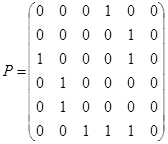 ;
;
4.
Вариант 20
1.  ;
;
2. 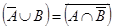 ;
;
3. 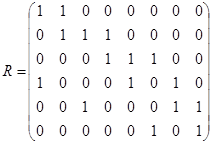 ;
;
4. 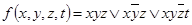 .
.
Вариант 21
1. 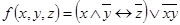 ;
;
2. 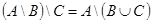 ;
;
3.  ;
;
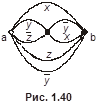
4.
Вариант 22
1. 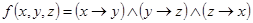 ;
;
2. 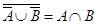 ;
;
3. 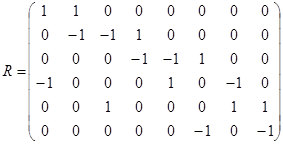 ;
;
4. 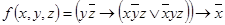 .
.
Вариант 23
1. 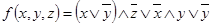 ;
;
2.  ;
;
3. 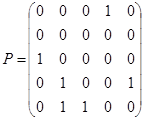 ;
;

4.
Вариант 24
1. 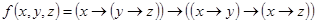 ;
;
2.  ;
;
3.  ;
;
4. 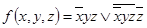 .
.
Вариант 25
1. 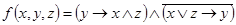 ;
;
2. 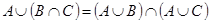 ;
;
3.  ;
;

4.
Вариант 26
1. 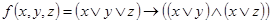 ;
;
2.  ;
;
3. 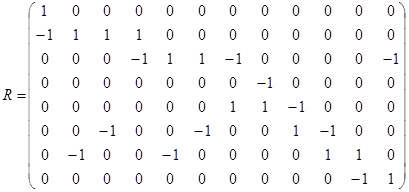 ;
;
4.  .
.
Вариант 27
1.  ;
;
2. 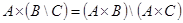 ;
;
3.  ;
;

4.
Вариант 28
1. 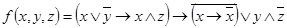 ;
;
2. 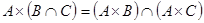 ;
;
3. 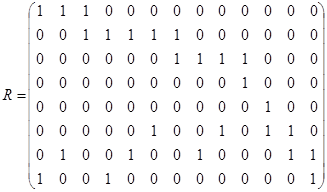 ;
;
4.  .
.
Вариант 29
1. 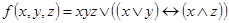 ;
;
2. если 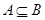 , то
, то 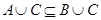 ;
;
3.  ;
;

4.
Вариант 30
1.  ;
;
2. если 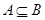 и
и 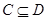 , то
, то  ;
;
3. 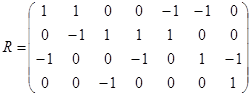 ;
;
4. 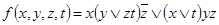 .
.
* Джордж Буль (1815-1864) – английский математик и логик.
– Конец работы –
Используемые теги: Эксцентриситет, вершины, Релейно-контактные, переключательные, схемы, Алгебра, высказываний, операции, над, множествами, Графы, способы, задания, графов, Релейно-контактные, схемы0.169
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Эксцентриситет вершины. Релейно-контактные (переключательные) схемы. Алгебра высказываний. Операции над множествами. Графы и Способы задания графов. Релейно-контактные схемы
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов