рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Нормы векторов и матриц
Реферат Курсовая Конспект
Нормы векторов и матриц
Нормы векторов и матриц - раздел Математика, Вычислительные методы линейной алгебры Приведем Определения Норм Векторов И Матриц [1]. Пусть Задан Вектор ...
Приведем определения норм векторов и матриц [1]. Пусть задан вектор x= (x1, x2, …, xn)T. Наиболее часто для векторов используются следующие нормы:
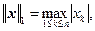 (3.1)
(3.1)
 (3.2)
(3.2)
 (3.3)
(3.3)
Норма (3.3) порождена скалярным произведением векторов
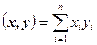 .
.
Для скалярного произведения справедливы следующие соотношения:
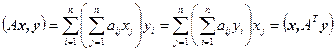 .
.
Если A симметричная матрица, то (Ax, y) = (x, Ay).
Определение 3.1. Нормой матрицы A называется число
 . (3.4)
. (3.4)
Согласованные с нормами векторов (3.1) — (3.3) нормы матриц определяются формулами
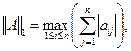 (3.5)
(3.5)
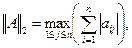 (3.6)
(3.6)
 (3.7)
(3.7)
Здесь  — собственные значения матрицы ATA, которая является симметричной. Чтобы обосновать формулу (3.7) рассмотрим определение нормы матрицы (3.4):
— собственные значения матрицы ATA, которая является симметричной. Чтобы обосновать формулу (3.7) рассмотрим определение нормы матрицы (3.4):

Можно доказать [1], что для симметричной матрицы B верно соотношение
 , (3.8)
, (3.8)
где λi — собственные значения матрицы B. Отсюда следует формула (3.7).
Пример 3.1. Вычислить нормы ||x||1, ||x||2, ||x||3 вектора x= (1, 2, – 3)T.
Решение. Пользуясь определениями норм (3.1) — (3.3), вычислим
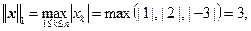
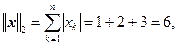

Пример 3.2. Вычислить нормы ||A||1, ||A||2, ||A||3 матрицы

Решение. По формулам (3.5), (3.6) находим нормы матриц


Чтобы вычислить норму матрицы по формуле (3.7) необходимо найти собственные значения матрицы, полученной умножением транспонированной матрицы AT на данную матрицу A:
 .
.
Не вдаваясь пока в подробности методов вычисления собственных значений матриц, вычислим в программе Mathcad собственные значения матрицы с помощью функции eigenvals:
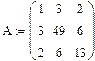
|
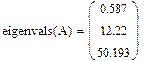
|
Теперь мы можем вычислить норму матрицы по формуле (3.7):
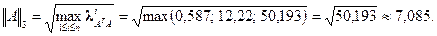
Определение 3.2. Две нормы ||x||α и ||x||β называются эквивалентными, если существуют постоянные γ1 и γ2 такие, что при всех x ≠ 0 справедливы соотношения
||x||α/||x||β ≤ γ1, ||x||β /||x||α ≤ γ2.
Нормы ||x||1, ||x||2, ||x||3 эквивалентны между собой, так как выполняются неравенства [1]
||x||1 ≤ ||x||3 ≤ ||x||2 ≤ n||x||1.
Из эквивалентности норм ||x||1, ||x||2, ||x||3 следует, что, если последовательность векторов сходится по одной из этих норм, то она сходится и по остальным нормам.
Ниже мы будем подразумевать под нормой ||x|| одну из указанных норм, а при необходимости конкретизировать, какую именно. При этом будем под нормой матрицы подразумевать норму, согласованную с нормой вектора.
– Конец работы –
Эта тема принадлежит разделу:
Вычислительные методы линейной алгебры
Вычислительные методы линейной алгебры изучают численные методы решения следующих задач... Решить систему линейных алгебраических уравнений СЛАУ... Вычислить определитель квадратной матрицы A...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Нормы векторов и матриц
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов