Итерационный метод

Запишем систему уравнений (3.9) в виде

 

Ax = b, (3.21)

где A — матрица коэффициентов, а b — вектор правых частей системы.

Преобразуем (3.21) к виду, удобному для итераций

x = Bx+ c. (3.22)

 

Тогда метод простой итерации определяется формулой:

x^{k +1} = Bx^k+ c, k = 0, 1, … (3.23)

 

где начальное приближение x⁰ задано.

Сформулируем теоремы об условиях сходимости метода простых итераций (доказательство теорем приведено в [1]).

Теорема 3.1(достаточное условие сходимости).Если ||B|| < 1, то система (3.21) имеет единственное решение, а итерационный метод (3.23) сходится к решению со скоростью геометрической прогрессии.

Теорема 3.2(необходимое и достаточное условие сходимости).Пусть система (3.22) имеет единственное решение. Итерационный процесс (3.23) сходится к решению системы (3.22) тогда и только тогда, когда все собственные значения матрицы B по модулю меньше единицы.

Теоремы 3.1 и 3.2 не дают способов преобразования произвольной системы линейных уравнений к виду (3.22) так, чтобы метод итераций (3.23) при этом сходился к решению. Эти теоремы имеют важное теоретическое значение. Отметим, что на практике для проверки условия сходимости метода итераций более полезна теорема 3.1, а теорему 3.2 удается использовать тогда, когда собственные значения матрицы B известны. Задача определения собственных значений матрицы в общем случае сложнее, чем решение системы линейных уравнений.

Для преобразования системы уравнений к виду, удобному для итераций можно [7] умножить систему (3.21) на матрицу D = A^–1 – ε, где ε — произвольная матрица. Тогда система примет вид (3.22)

 

x = Bx+ c, B = εA, c = Db (3.24)

 

и матрица B будет удовлетворять теореме (3.1), если выбрать элементы матрицы ε достаточно малыми по модулю. Однако, этот прием не выгоден, так как для вычисления обратной матрицы A^–1 необходимо выполнить не меньше операций, чем на решение самой системы.

При небольшом числе уравнений систему иногда удается привести к виду, удобному для итераций с помощью нескольких преобразований. Пример, иллюстрирующий этот способ, содержится в [7].

Ниже, в последующих главах, будут рассмотрены разностные методы решения краевых задач для обыкновенных дифференциальных уравнений и уравнений в частных производных, которые приводят к решению систем линейных уравнений с большим числом неизвестных. Учитывая специфику таких систем, часто удается построить эффективные итерационные методы решения.

Пример 3.4.Система линейных уравнений приведена к виду, удобному для итераций. Проверить условия сходимости и найти решения.

 

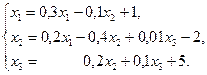
Решение.Найдем норму матрицы B и проверим условие сходимости

 

.

 

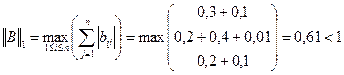По теореме 3.1 мы имеем сходящийся итерационный процесс:

 

 

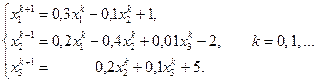
Выберем в качестве начального приближения вектор свободных членов x⁰ = (1, –2, 5)^T и проведем вычисления в программе Excel.

1) В ячейки A2:C4 введем элементы матрицы B, а в ячейки F2:F4 — свободные члены, как показано в таблице 3.3.

2) В столбце D будем вычислять последовательные приближения к решению. В ячейках D2: D4 запишем начальное приближение, т.е. введем числовые значения компонент вектора x⁰: 1, –2, 5. Выделим диапазон D5: D7, введем формулу =МУМНОЖ(A$2:C$4;D2:D4)+F$2:F$4 и, удерживая нажатыми клавиши Ctrl и Shift, нажмем Enter. В ячейках D5: D7 появятся значения компонент вектора x¹. Выделим D5: D7 и с помощью мыши протянем маркер заполнения вниз до D22. Здесь надо иметь ввиду, что в ячейках D5: D7 записана операция с массивом, поэтому число новых строк, в которые копируем эти ячейки, должно быть кратно 3. В нашем случае имеем 15 строк, т.е. 5 новых итераций, а всего, с учетом D5: D7, выполнено 6 итераций.

3) В столбце E вычислим разности между компонентами последовательных приближений x^k и x^{k +1}. Выделим диапазон E5: E7, введем формулу =ABS(D2:D4-D5:D7), и протянем маркер заполнения вниз до E22. В ячейках
E20: E22 максимальное число равно 0,0067 = ||x^{k +1} – x^k||₁, что соответствует приблизительно погрешности 0,01. Решение системы

 

x₁ ≈ 1,59; x₂ ≈ – 1,16; x₃ ≈ 5,29.

 

В табл. 3.3 показано содержимое ячеек A1: F7 в режиме формул, которое высвечивается, если выполнить команду меню «Сервис — параметры», выбрать вкладку «Вид» и отметить в параметрах окна флажком пункт «формулы». Если этот флажок снять, то увидим вычисленные компоненты решения.

Таблица 3.3

	A	B	C	D	E	F
				Вектор Xk	Разность
	0,3	-0,1
	0,2	-0,4	0,01	-2		-2
		0,2	0,1
				=МУМНОЖ(A$2:C$4;D2:D4)+F$2:F$4	=ABS(D2:D4-D5:D7)
				=МУМНОЖ(A$2:C$4;D2:D4)+F$2:F$4	=ABS(D2:D4-D5:D7)
				=МУМНОЖ(A$2:C$4;D2:D4)+F$2:F$4	=ABS(D2:D4-D5:D7)

 

Составим программу на языке C++ для решения системы уравнений методом итераций:

 

#include <except.h>

#include <iostream.h>

#include <math.h>

int iter(long double **b, long double *c, long double *x,

long double eps, int k_max, const int n);

int main(){

long double **b; long double *c, *x, eps; int i,j,n,k_max;

cout <<"n input n = " ; cin >> n;

cout <<"n input eps = " ; cin >> eps;

cout <<"n input k_max = " ; cin >> k_max;

try {

b= new long double*[n]; for(i=0;i<n;i++) b[i]=new long double[n];

c= new long double[n]; x= new long double[n];

}

catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}

cout <<"n input matrix b n";

for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> b[i][j];

cout <<"n input vector cn";

for (i=0; i<n; i++)cin >> c[i];

cout << "n matrix b: ";

for (i=0; i<n; i++){cout << "n"; for (j=0; j<n; j++) cout <<" "<< b[i][j];}

cout << "n vector c: ";

for (i=0; i<n; i++)cout << "n " << c[i];

iter(b, c, x,eps,k_max, n);

cout << "n vector x: ";

for (i=0; i<n; i++)cout << "n x[" << i <<"] = " << x[i];

cout << "n Press Key and Enter to continue";

cin >> i; // for pause

for(i=0;i<n;i++)delete[] b[i];

delete b;

delete[] c;

delete[] x;

return 0;

}//end main

int iter(long double **b, long double *c, long double *x,

long double eps, int k_max, const int n){

int i, j, m; long double *x1, xerr;

try {x1 = new long double[n];}

catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}

for (m = 0; m <= k_max; m++) {// m

for (i = 0; i < n; i++){

x1[i] = c[i]; for (j = 0; j < n; j++) x1[i] = x1[i] + b[i][j]*x[j];}

xerr = 0;

for (i = 0; i < n; i++) xerr = xerr + (x1[i] - x[i])* (x1[i] - x[i]);

xerr = sqrt(xerr);

for (i = 0; i < n; i++) x[i] = x1[i]; if(xerr < eps) break;

}// end m

delete[] x1;

return 0;

}// end iter

 

Найдем с помощью этой программы решение системы уравнений примера 3.4:

 

input n = 3

input eps = 0.00001

input k_max = 10000

input matrix b

0.3 –0.1 0 0.2 –0.4 0.01 0 0.2 0.1

Input vector c

1 –2 5

matrix b:

0.3 –0.1 0

0.2 –0.4 0.01

0 0.2 0.1

vector c:

–2

vector x:

x[0] = 1.5947

x[1] = –1.16292

x[2] = 5.29713

Press Key and Enter to continue

 

Как видим, решение совпадает с решением, полученным в программе Excel.