Вычисление определителя и обратной матрицы

Вычисление определителя матрицы является классическим примером задач, для решения которых важно найти эффективные алгоритмы.

При непосредственном раскрытии определителя квадратной матрицы n-го порядка надо найти сумму n! слагаемых, каждое из которых равно произведению n элементов матрицы, взятых по одному с каждого столбца и каждой строки, т.е. надо выполнить порядка n!n операций. Число операций для вычисления определителя 100-го порядка приблизительно равно 100!∙100 ≈ 100^157,9∙100. Такое число операций не способен выполнить ни один из существующих суперкомпьютеров. Тем не менее, современные компьютерные программы вычисления определителей справляются с матрицами и более высокого порядка, используя экономичные алгоритмы. Одним из таких алгоритмов является метод Гаусса.

Если матрица приведена к диагональному или треугольному виду, то её определитель равен произведению диагональных элементов.

Для преобразования матрицы к треугольному виду можно применить метод Гаусса, что потребует порядка 2n³/3 операций. Для n = 100 имеем 2n³/3 ≈ 0,67∙10⁶. На такой объем арифметических операций современный персональный компьютер тратит не более одной секунды.

Если внимательно проанализировать метод Гаусса, то можно увидеть, что он фактически позволяет одновременно с приведением матрицы коэффициентов к треугольному виду, вычислить определитель этой матрицы. Действительно, определитель матрицы коэффициентов системы уравнений (3.18) равен произведению диагональных элементов, т.е. равен единице. С другой стороны, если к любой строке матрицы прибавить другую строку, умноженную на число, то определитель не изменится. А если строку матрицы разделить на число, отличное от нуля, то определитель матрицы разделится на то же число. Отсюда следует, что в результате преобразований виду (3.18), определитель матрицы коэффициентов системы уравнений (3.9) изменился на множитель, который равен произведению ведущих элементов, т.е. мы получаем формулу для вычисления определителя

 

.

 

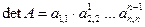Метод Гаусса также эффективен и для вычисления обратной матрицы. Вычисление обратной матрицы можно рассматривать как частный случай решения совокупности систем линейных уравнений с одной и той же матрицей коэффициентов и разными правыми частями. В этом случае преобразования, которые применяются к столбцу b правых частей системы, нужно применить к нескольким столбцам правых частей.

Пример 3.8. Для заданной матрицы вычислить определитель и обратную матрицу.

 

.

 

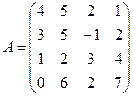Решение.Используем рабочий лист решения примера 3.3. Введем элементы данной матрицы в диапазоне A2:D5.

В ячейке G17 вычислим произведение ведущих элементов (т.е. тех чисел, на которые делили строки), для этого введем формулу =A2*B7*C12*D17. В ячейку F17 введем формулу =МОПРЕД(A2:D5) и убедимся в правильности результата. Получим значение –190.

Для вычисления обратной матрицы используем новый рабочий лист.

Рассмотрим расширенную матрицу

 

 

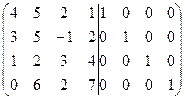
Мы должны преобразовать методом Гаусса исходную матрицу к единичной, тогда единичная матрица справа от вертикальной черты преобразуется к обратной матрице.

Прямой ход метода Гаусса.

0. Запишем элементы матрицы в диапазоне A2:D5 и элементы единичной матрицы в диапазоне E2:H5.

1. В ячейку A7 вводим формулу =A2/$A2; выделим A7 и протянем маркер заполнения до ячейки H7.

Затем в ячейку A8 вводим формулу =A3-A$7*$A3; выделим A8 и протянем маркер заполнения до H8.

Выделим строку A8:H8 и протянем маркером заполнения вниз до строки 10.

В ячейках A7:HE10 появятся следующие значения:

1,0000	1,2500	0,5000	0,2500	0,2500	0,0000	0,0000	0,0000
0,0000	1,2500	-2,5000	1,2500	-0,7500	1,0000	0,0000	0,0000
0,0000	0,7500	2,5000	3,7500	-0,2500	0,0000	1,0000	0,0000
0,0000	6,0000	2,0000	7,0000	0,0000	0,0000	0,0000	1,0000

 

2. Присвоим строке A12:H12 значения строки A7:H7:

Выделим диапазон A12:H12, введем формулу =A7:H7 и удерживая нажатыми клавиши Ctrl и Shift, нажимаем Enter (Ctrl + Shift + Enter).

В ячейку B13 вводим формулу =B8/$B8; выделим B13 и протянем маркер заполнения до H13.

Затем в ячейку B14 вводим формулу =B9-B$13*$B9; выделим B14 и протянем мышью маркер заполнения до H14.

Выделим диапазон B14:H14 и протянем маркер заполнения до H15.

В ячейках A12:H15 появятся следующие значения:

 

1,0000	1,2500	0,5000	0,2500	0,2500	0,0000
0,0000	1,0000	-2,0000	1,0000	-0,6000	0,8000	0,0000	0,0000
	0,0000	4,0000	3,0000	0,2000	-0,6000	1,0000	0,0000
	0,0000	14,0000	1,0000	3,6000	-4,8000	0,0000	1,0000

 

3. Перепишем значения строк A12:H15 в строки A17:H18, для этого выделим диапазон A12:H15, введем формулу =A12:H13 и удерживая клавиши Ctrl и Shift нажатыми, нажимаем Enter.

В ячейку C19 вводим формулу =C14/$C14; выделим C19 и протянем мышью за правый нижний угол до H19.

В ячейку C20 вводим формулу =C15-C$19*$C15, выделим C20 и протянем маркер заполнения до H20. В ячейках A17:H20 получим значения:

 

1,0000	1,2500	0,5000	0,2500	0,2500	0,0000
0,0000	1,0000	-2,0000	1,0000	-0,6000	0,8000
		1,0000	0,7500	0,0500	-0,1500	0,2500	0,0000
		0,0000	-9,5000	2,9000	-2,7000	-3,5000	1,0000

 

4. Осталось разделить последнюю строку на ведущий элемент. Сформируем в диапазоне A22:H25 матрицы, которые получаются после применения прямого хода метода Гаусса.

Выделим диапазон A22:H24 и введем формулу =A17:H19 и, удерживая нажатыми клавиши Ctrl и Shift, нажимаем Enter. В ячейку D25 вводим формулу =D20/$D20, выделим D25 и протянем мышью за правый нижний угол до H25. В диапазоне A22:H25 получим:

 

1,0000	1,2500	0,5000	0,2500	0,2500	0,0000
0,0000	1,0000	-2,0000	1,0000	-0,6000	0,8000
0,0000	0,0000	1,0000	0,7500	0,0500	-0,1500	0,25
			1,0000	-0,3053	0,2842	0,3684	-0,1053

 

Далее применим обратный ход метода Гаусса.

5. Выделим A30:H30, введем =A25:H25 и нажмем комбинацию клавиш Ctrl + Shift + Enter. В ячейку D29 введем =D24-D$25*$D24, выделим D29 и протянем маркер заполнения вправо до H29. А затем снова выделим D29 и протянем маркер заполнения влево до A29. Теперь выделим всю строку A29:H29 и протянем вверх до строки 27.

6. Выделим A34:H35, введем =A29:H30 и нажмем комбинацию клавиш Ctrl + Shift + Enter. В ячейку C33 введем =C28-C$34*$C28, выделим C33 и протянем маркер заполнения вправо до H33. А затем снова выделим C33 и протянем маркер заполнения влево до A33. Теперь выделим всю строку A33:H33 и протянем маркером заполнения на одну строку вверх до строки 32.

7. Выделим A38:H40, введем формулу =A33:H35 и нажмем комбинацию клавиш Ctrl + Shift + Enter. В ячейку B37 введем формулу =B32-B$38*$B32, выделим B37 и протянем маркер заполнения вправо до H37. Затем снова выделим B37 и протянем маркер заполнения влево в ячейку A37.

В диапазоне A37:D40 получена единичная матрица, а в диапазоне E37:H40 — обратная:

 

	A	B	C	D	E	F	G	H
					-0,14211	0,373684	0,447368	-0,34211
					0,263158	-0,21053	-0,42105	0,263158
					0,278947	-0,36316	-0,02632	0,078947
					-0,30526	0,284211	0,368421	-0,10526

 

Для проверки полученного результата выделим диапазон A43:D46, введем формулу =МУМНОЖ(A2:D5;E37:H40) и нажмем комбинацию клавиш Ctrl + Shift + Enter. Получим единичную матрицу.

Приведем программу на языке C++ для вычисления определителя матрицы методом Гаусса с выбором главного элемента.

 

#include <except.h>

#include <iostream.h>

long double detA(long double **a, const int n);

int main(){

long double **a; long double dA; int i,j,n;

cout <<" input n = " ; cin >> n;

try {

a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n];

}

catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}

cout <<"n input matrix a n";

for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j];

dA = detA(a, n);

cout << "n matrix a: ";

for (i=0; i<n; i++){cout << "n"; for (j=0; j<n; j++) cout <<" "<< a[i][j];}

cout << "n determinant A = "; cout << dA;

cout << "n Press Key and Enter to continue";

cin >> i; // for pause

for(i=0;i<n;i++)delete[] a[i];

delete a;

return 0;

}//end main

long double detA(long double **a, const int n){

long double **aa;

int i, k, m, im; long double amm, aim, r,d;

try {aa= new long double*[n];

for(i=0;i<n;i++) aa[i]=new long double[n]; }

catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}

for (i = 0; i <= n-1; i++)

for (k = 0; k <= n-1; k++) aa[i][k] = a[i][k];

d = 1;

for (m = 0; m <= n-2; m++) {// m

amm = aa[m][m]; im = m;

for (i = m; i <= n-1; i++)

if(aa[i][m] > amm){amm = aa[i][m]; im = i; } d = d*amm;

if(im != m)d = - d;

cout <<"n amm = "<<amm;

if(im != m)for (k = m; k <= n-1; k++)

{r = aa[im][k]; aa[im][k] = aa[m][k]; aa[m][k] = r;}

for (k = m; k <= n-1; k++)aa[m][k] = aa[m][k]/amm; // 3.16

for (i = m + 1; i <= n-1; i++){// i

aim = aa[i][m];

for (k = m; k <= n-1; k++)

aa[i][k] = aa[i][k] - aa[m][k]*aim; // 3.17

}// end i

}// end m

d = d* aa[n-1][n-1]; cout <<"n amm = "<< aa[n-1][n-1];

for(i=0;i<n;i++)delete[] aa[i];

delete aa;

return d;

}// end detA

 

Отметим, что в данной программе исходная матрица a[][] сохраняется, так как для преобразований в подпрограмме-функции detA() используется дополнительный массив aa[][]. Все используемые массивы динамические, их размерность задается во время выполнения программы.

Приведем результат расчета определителя по этой программе:

 

input n = 4

input matrix a

4 5 2 1 3 5 -1 2 1 2 3 4 0 6 2 7 [столбец чисел ]

amm = 4

amm = 6

amm = 2.25

amm = 3.51852

matrix a:

4 5 2 1

3 5 -1 2

1 2 3 4

0 6 2 7

Determinant A = –190

Press key and Enter to continue

 

Приведем теперь программу вычисления обратной матрицы методом Гаусса с выбором главного элемента:

 

#include <except.h>

#include <iostream.h>

int Matr_inv(long double **a, long double **a1, const int n);

int main(){

long double **a; long double **ainv; int i,j,n;

cout <<" input n = " ; cin >> n;

try {

ainv= new long double*[n]; for(i=0;i<n;i++) ainv[i]=new long double[n];

}

catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}

try {

a= new long double*[n]; for(i=0;i<n;i++) a[i]=new long double[n];

}

catch (xalloc){cout <<"nCould not allocaten"; exit(-1);}

cout <<"n input matrix a n";

for (i=0; i<n; i++)for (j=0; j<n; j++)cin >> a[i][j];

cout << "n matrix a: ";

for (i=0; i<n; i++){cout << "n";

for (j=0; j<n; j++) cout <<" "<< a[i][j];}

Matr_inv(a, ainv, n);

cout << "n ------------------- matr a: ";

for (i=0; i<n; i++){cout << "n";

for (j=0; j<n; j++) cout <<" "<< a[i][j];}

cout << "n -------------------- inv matr ainv: ";

for (i=0; i<n; i++){cout << "n";

for (j=0; j<n; j++) cout <<" "<< ainv[i][j];}

cout << "n Press Key and Enter to continue";

cin >> i; // for pause

for(i=0;i<n;i++)delete[] a[i];

delete a;

for(i=0;i<n;i++)delete[] ainv[i];

delete ainv;

return 0;

}//end main

int Matr_inv(long double **a, long double **a1, const int n){

int i, k, m, im; long double amm, aim, r;

for (i = 0; i <= n-1; i++)

for (k = 0; k <= n-1; k++){

if(i==k)a1[i][k] = 1; else a1[i][k] = 0;}

// 1.

for (m = 0; m <= n-2; m++) {// m

amm = a[m][m]; im = m;

for (i = m; i <= n-1; i++)

if(a[i][m] > amm){amm = a[i][m]; im = i; }

if(im != m){

for (k = m; k <= n-1; k++){

r = a[im][k]; a[im][k] = a[m][k]; a[m][k] = r;}

for (k = 0; k <= n-1; k++){

r = a1[im][k]; a1[im][k] = a1[m][k]; a1[m][k] = r;}

}

for (k = m; k <= n-1; k++)a[m][k] = a[m][k]/amm;

for (k = 0; k <= n-1; k++) a1[m][k] = a1[m][k]/amm;

for (i = m + 1; i <= n-1; i++){// i

aim = a[i][m];

for (k = m; k <= n-1; k++)a[i][k] = a[i][k] - a[m][k]*aim;

for (k = 0; k <= n-1; k++)a1[i][k] = a1[i][k] - a1[m][k]*aim;

}// end i

}// end m

// 2.

amm = a[n-1][n-1]; a[n-1][n-1] = 1;

for (k = 0; k <= n-1; k++) a1[n-1][k] = a1[n-1][k]/amm;

for (m = n-1; m >= 0; m--){

for (i = m-1; i >= 0; i--){// i

aim = a[i][m]; a[i][m] = 0;

for (k = 0; k <= n-1; k++)a1[i][k] = a1[i][k] - a1[m][k]*aim;

}// end i

}// end m

return 0;

}// end Matr_inv

 

Подпрограмма Matr_inv(a, a1, n) не сохраняет исходную матрицу. В результате выполнения программы в массиве a формируется единичная матрица, а в массиве a1 — обратная матрица. Приведем результат выполнения программы для примера 3.8:

 

input n = 4

input matrix a

4 5 2 1 3 5 -1 2 1 2 3 4 0 6 2 7 [столбец чисел ]

matrix a

4 5 2 1

3 5 -1 2

1 2 3 4

0 6 2 7

---------------------------- matr a

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 0

---------------------------- inv matr ainv

-0,142105 0,373684 0,447368 -0,342105

0,263158 -0,210526 -0,421053 0,263158

0,278947 -0,363158 -0,0263158 0,0789474

-0,305263 0,284211 0,368421 -0,105263

Press Key and Enter to continue

 

Как видим, результат совпадает с обратной матрицей, найденной в программе Excel обычным методом Гаусса.