Задача 10.

Прогнозирование на основе сглаженного временного ряда

Динамика удельного расхода условного топлива на производство тепло-энергии (yt, кг/Гкал) на ТЭЦ по годам представлена в таблице. Требуется:

1)произвести сглаживание ряда методом трехлетней скользящей средней;

2)выровнять ряд по прямой - т.е. оценить параметры bo,b1 линейного
тренда 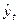= b0 + b1t методом наименьших квадратов;

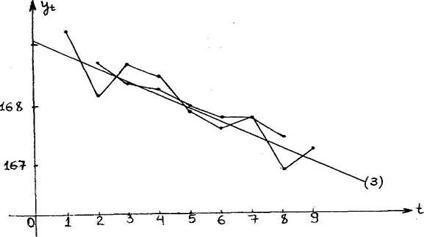
3)начертить графики первичного и сглаженных рядов;

4)на уровне значимости α = 0,05 проверить согласованность линейной
трендовой модели с результатами наблюдений;

5)методом экстраполяции найти точечные и интервальные (с доверитель­
ной вероятностью γ = 0,95) оценки прогноза экономического показателя yt на
2002 и 2003г.г.

yt 169,2 168,1 168,6 168,4 167,9 167,6 167,8 166,9 167,1

(n=9)
Временным рядом называется последовательность значений (уровней) не­которого экономического показателя yt, расположенных в порядке возрастания времени. Уровни ряда должны отражать значения экономического показателя за одинаковые или через одинаковые промежутки времени.

Одной из важнейших задач исследования временного ряда является задача выявления основной тенденции развития (тренда) изучаемого процесса.

Решение этой задачи необходимо для прогнозирования. При этом исходят из того, что тенденция развития, установленная в прошлом, может быть распространена (экстраполирована) на будущий период.

Наиболее простыми и часто применяемыми способами выявления основ­ной тенденции развития являются сглаживание временного ряда методом скользящей средней или выравнивание по прямой методом наименьших квадратов.

1) Метод скользящей средней основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени "скользит" вдоль ряда, получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд.

Для нашего примера скользящие средние находим по формуле

.

Например, при t = 2

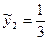(169,2 +168,1 +168,9)168,7,

при t = 3 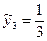(168,1 +168,9 +168,4) 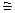168,5.

По результатам получим сглаженный ряд:

yt – 168,6 168,4 168,3 168,0 167,8 167,8 167,3 –

 

2) По статистическим данным найдем оценки и параметров линейно­го тренда 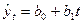методом наименьших квадратов. Для этого применим из­вестные формулы [1]:

,

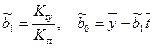где .

Здесь и в дальнейшем t - номер уровня ряда: 1993 г. соответствует номер 1,... 2001 году - номер 9.

Вычисление средних значений 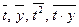организуем в форме расчетной таблицы.

 

 

 

 

 

 

 

 

 

 

  yt
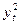
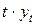
169,2 28628,64 169,2
168,1 28257,61 336,2
168,6 28425,96 505,8
168,4 28358,56 673,6
167,9 28190,41 839,5
167,6 28089,76 1005,6
167,8 28156,84 1174,6
166,9 27855,61 1335,2
167,1 27922,41 1503,9
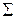
1511,6 253885,8 7543,6
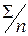
167,955 31,67 28209,53 838,18
 

 

.

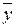
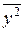
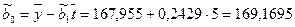Таким образом, искомые оценки параметров линейного аренда равны: = 169,1695, = -0,2429. Уравнение линейного тренда имеет вид:

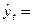169,1695 - 0,2429·t.

3)

 
 

(2)
На рисунке цифрой (1) отмечен первичный ряд, цифрой (2) - скользящая трехлетняя средняя, цифрой (3) помечен ряд, выровненный по прямой.

 
 
(1)


(1)
4) Проверка согласованности линейной трендовой модели с результатами наблюдений выполняется как решение задачи проверки статистической гипотезы об отсутствии линейной статистической связи переменных 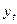и t на заданном уровне значимости α = 0,05. Для проверки гипотезы используется коэффициент детерминации 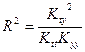и применяется статистика Фишера с и к2=п - 2 степенями свободы.

 

В рассматриваемом случае 28209,53 - (167,955)2 = 0,648, , .

Критическое значение статистики Фишера равно

.

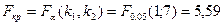Так как 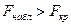, то выдвинутая гипотеза Hо отвергается, что свидетельствует о согласии линейной трендовой модели с результатами наблюдений.

5) По полученному уравнению линейного тренда 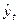=169,1695- 0,2429 t найдем точечные (индивидуальные) прогнозы показателя 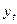на 2002 и 2003 г.г.

Для 2002г. t = 10

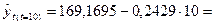166,7405.

Для 2003г. t = 11

166,4976.

Дать интервальную оценку тренда - значит указать границы интервала, в который попадет возможное значение переменной с заданной доверитель­ной вероятностью γ (в нашем примере γ = 0,95).

Этот интервал определяется по известным формулам [3]

,

где δ - точность прогноза , здесь к=п-2 - число степеней свободы, α=1-γ, ищется по таблице критических точек распределения Стьюдента для двусторонней критической области (см., например [4]); в нашем случае α=1 - 0,95 = 0,05; к = 9-2 =7; 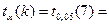2,36. (Можно воспользоваться так же таблицами [3]). 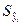- исправленное среднеквадратическое отклонение (С.К.О.) индивидуальных значений зависимой переменной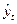

.

 

Из этой формулы видно, чем больше , тем меньше точность прогноза. S - исправленное С.К.О. ошибок линейной регрессии

.

Вычисление доверительных интервалов прогнозов организуем в виде таблицы

t yt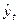
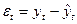
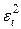
169,2 168,9266 0,2734 0,07475
168,1 168,6837 -0,5837 0,34071
168,6 168,4408 0,1592 0,02534
168,4 168,1979 0,2021 0,04084
167,9 167,9550 -0,055 0,00303
167,6 167,7121 -0,1121 0,01257
167,8 167,4692 0,3308 0,10943
166,9 167,2263 -0,3263 0,10647
167,1 166,9834 0,1166 0,01360
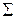
– – – 0,72674

.

.

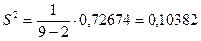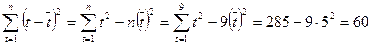Дальнейшие вычисления проводим отдельно для t =10 (2002 г.) и t =11 (2003 г.)

Для t = 10

.

,

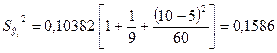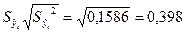
166,74-0,94<<166,74+0,94.

Итак, с вероятностью γ = 0,95, удельный расход условного топлива в 2002 г. будет принадлежать интервалу (кг/Гкал)

165,8 << 167,68.

Аналогично для 2003 г. t = 11, получим

. , ,

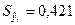166,498-0,995<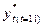<166,498+0,995. 165,50<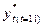<167,49, γ=0,95.