Задача 10.
Динамика удельного расхода условного топлива на производство теплоэнергии ( , кг/Гкал) на ТЭЦ по городам представлена в таблице.
, кг/Гкал) на ТЭЦ по городам представлена в таблице.
Требуется:
1) произвести сглаживание ряда методом трехлетней скользящей средней;
2) выровнять ряд по прямой;
3) методом экстраполяции определить прогноз экономического показателя 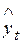 на 2002 и 2003 г.г.;
на 2002 и 2003 г.г.;
4) начертить графики первичного и выроненного рядов.
10.1.
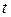
| |||||||||

| 167,6 | 165,8 | 167,4 | 168,0 | 167,5 | 167,2 | 166,5 | 166,5 | 166,4 |
10.2.
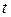
| |||||||||

| 169,1 | 167,3 | 168,9 | 169,5 | 169,0 | 168,7 | 168,0 | 168,0 | 167,9 |
10.3.
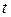
| |||||||||

| 166,1 | 164,3 | 165,9 | 166,5 | 166,0 | 165,7 | 165,0 | 165,0 | 164,9 |
10.4.
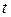
| |||||||||

| 168,6 | 166,8 | 168,4 | 169,0 | 168,5 | 168,2 | 167,5 | 167,5 | 167,4 |
10.5.
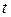
| |||||||||

| 166,6 | 164,8 | 166,4 | 167,0 | 166,5 | 166,2 | 165,5 | 165,5 | 165,4 |
10.6.
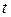
| |||||||||

| 168,1 | 166,3 | 167,9 | 168,5 | 168,0 | 167,7 | 167,0 | 167,0 | 166,9 |
10.7.
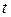
| |||||||||

| 170,1 | 168,3 | 169,9 | 170,5 | 170,0 | 169,7 | 169,0 | 169,0 | 168,9 |
10.8.
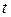
| |||||||||

| 165,6 | 163,8 | 165,4 | 166,0 | 165,5 | 165,2 | 164,5 | 164,5 | 164,4 |
10.9.
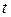
| |||||||||

| 169,6 | 167,8 | 169,4 | 170,0 | 169,5 | 169,2 | 168,5 | 168,5 | 168,4 |
10.10.
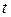
| |||||||||

| 169,1 | 167,3 | 168,9 | 169,5 | 169,0 | 168,7 | 168,0 | 168,0 | 167,9 |
Методические указания к выполнению контрольной работы.
Решение типовых задач.
Задача 1.
Из генеральной совокупности  , распределенной по нормальному закону, извлечена выборка. Требуется:
, распределенной по нормальному закону, извлечена выборка. Требуется:
1. Составить вариационный, статистический и выборочный ряды распределения; найти размах выборки;
По полученному распределению выборки:
2. Построить полигон относительных частот;
3. Построить график эмпирической функции распределения;
4. Вычислить выборочную среднюю, выборочную дисперсию, выборочное исправленное среднее квадратическое отклонение, моду и медиану;
5. С надежностью  найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
найти доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
1.0. 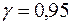
| 5,6 | 5,8 | 5,0 | 5,4 | 5,2 | 5,8 | 5,2 | 5,6 |
| 5,6 | 5,6 | 5,4 | 5,0 | 5,4 | 5,8 | 5,4 | 5,6 |
| 5,4 | 5,2 | 5,4 | 5,4 | 5,6 | 5,0 | 6,0 | 5,8 |
| 5,2 | 5,8 | 5,6 | 5,8 | 6,0 | 5,2 | 5,8 | 6,0 |
| 6,2 | 5,4 | 6,2 | 5,6 | 6,0 | 5,6 | 5,2 | 5,6 |
Составим вариационный ряд. Напомним, что вариационным рядом называется последовательность наблюдаемых значений признака  , расположенных в неубывающем порядке
, расположенных в неубывающем порядке 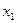 ,
, ,…,
,…,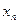 , где
, где 
 …
…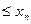 . Следовательно, в нашей задаче вариационный ряд запишется так:
. Следовательно, в нашей задаче вариационный ряд запишется так:
| 5,0 | 5,0 | 5,0 | 5,2 | 5,2 | 5,2 | 5,2 | 5,2 |
| 5,2 | 5,4 | 5,4 | 5,4 | 5,4 | 5,4 | 5,4 | 5,4 |
| 5,4 | 5,6 | 5,6 | 5,6 | 5,6 | 5,6 | 5,6 | 5,6 |
| 5,6 | 5,6 | 5,6 | 5,8 | 5,8 | 5,8 | 5,8 | 5,8 |
| 5,8 | 5,8 | 6,0 | 6,0 | 6,0 | 6,0 | 6,2 | 6,2 |
Составим статистический ряд распределения данной нам выборки
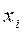
| 5,0 | 5,2 | 5,4 | 5,6 | 5,8 | 6,0 | 6,2 |

|
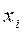 - варианты,
- варианты,  - частоты.
- частоты.
Найдем объем выборки
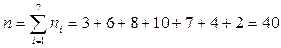 .
.
Относительная частота вычисляется по формуле  .
.
Запишем выборочный ряд распределения
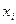
| 5,0 | 5,2 | 5,4 | 5,6 | 5,8 | 6,0 | 6,2 |

| 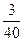
| 
| 
| 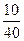
| 
| 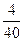
| 
|

 .
.
Размах выборки  , т.е. в нашем случае
, т.е. в нашем случае 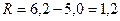 .
.
 |
Построим полигон относительных частот
Вычислим выборочную среднюю
 = =
= = (
(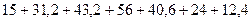 )=
)=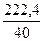 =5,56.
=5,56.
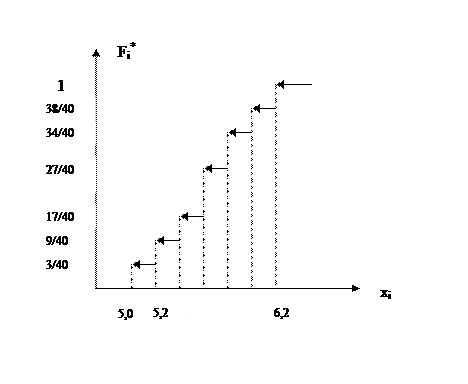
Построим график эмпирической функции распределения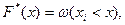 где
где 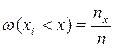 (
(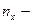 число вариант, меньших, чем значение аргумента
число вариант, меньших, чем значение аргумента 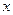 ).
).
Вычислим выборочную дисперсию , где в нашем случае
, где в нашем случае  =
= (
(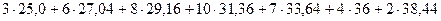 )=
)= =31,012
=31,012

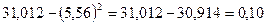 .
.
Найдем выборочное среднее квадратическое отклонение
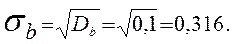
Вычислим "исправленную" дисперсию 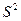 , которая выражается формулой
, которая выражается формулой
 (в нашем случае
(в нашем случае  )
)
и "исправленное" среднее квадратическое отклонение  .
.
Модой  называется варианта с наибольшей частотой, т.е. в нашей задаче
называется варианта с наибольшей частотой, т.е. в нашей задаче  . Медиана
. Медиана 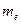 - варианта, которая делит вариационный ряд на две части, равные по числу вариант, т.е. в нашей задаче
- варианта, которая делит вариационный ряд на две части, равные по числу вариант, т.е. в нашей задаче 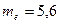 .
.
Найдем с надежностью g=0,95 доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения изучаемого признака генеральной совокупности.
Так как по условию задачи генеральная совокупность x распределена по нормальному закону и объем выборки равен n=40, то искомый доверительный интервал для оценки математического ожидания имеет вид
 ,
,
где  - среднее квадратическое отклонение, а величина t определяется по таблице значений функции Лапласа из равенства
- среднее квадратическое отклонение, а величина t определяется по таблице значений функции Лапласа из равенства 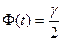 .
.
Следовательно, в нашем случае последнее равенство принимает вид 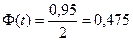 . Из этого равенства по таблице значений интегральной функции Лапласа
. Из этого равенства по таблице значений интегральной функции Лапласа  находим значение t=1,96. Величина
находим значение t=1,96. Величина  была найдена ранее:
была найдена ранее:  и
и  .
.
Вычислим  .
.  .
.
Учитывая, что 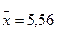 , доверительный интервал для оценки математического ожидания запишется
, доверительный интервал для оценки математического ожидания запишется 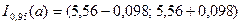 или, окончательно,
или, окончательно, 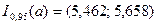 .
.
Доверительный интервал для среднего квадратического отклонения нормально распределенной случайной величины находится по формуле 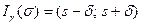 , где s - "исправленное" среднее квадратическое отклонение, а d находится по формуле
, где s - "исправленное" среднее квадратическое отклонение, а d находится по формуле 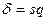 , где величина q определяется по специальной таблице значений функции
, где величина q определяется по специальной таблице значений функции 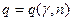 .
.
Найдем  для нашей конкретной задачи:
для нашей конкретной задачи:
q=q(0,95;40)=0,24; d=sq=0,321×0,24=0,077. Следовательно,  или окончательно
или окончательно  .
.
На этом решение задачи 1 закончено.