Свойства определителя

1) Определитель транспонированной матрицы равен определителю исходной

Доказательство: обозначим , , 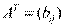где 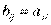. Тогда по определению:

Теперь упорядочим множители 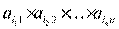по i индексам: 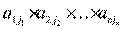. В результате такой перестановки, очевидно, не изменится ни число инверсий перестановки , ни число самих перестановок, так как просто меняются местами сами строки перестановки 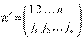. Поэтому имеем:

 

 

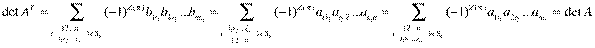
Отсюда и получается .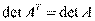

Следствие: принцип равноправия строк и столбцов: все свойства, доказанные для строк определителя верны и для его столбцов.

2) Общий для всех элементов строки множитель можно выносить за знак определителя

Доказательство: Пусть, для определённости, строка с номером k имеет общий для всех элементов множитель . По определению имеем: .

При этом в каждое произведение вида входит по одному элементу из каждой строки, а стало быть, и из строки с номером k:

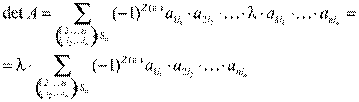
Что и требовалось.

Следствие: если матрица содержит нулевую строку (столбец), её определитель равен нулю.

Доказательство: в доказательстве свойства (2) достаточно положить

3) При сложении двух определителей, различающихся только одной строкой, элементы этой строки складываются.

Доказательство: пусть имеются две матрицы порядка n, различающиеся лишь k-ой строкой:

Тогда сумма их определителей:

Следствие: из свойств (2) и (3) следует линейность определителя как функции матрицы.

4) Если в матрице две строки поменять местами, то определитель сменит знак.

Доказательство: пусть, для начала, мы поменяли местами соседние строки. Например, i-ую и (i+1)-ую. Рассмотрим, какие изменения это повлечет в записи определителя исходной матрицы:

Произведения будут отличаться лишь порядком сомножителей, но перестановка отличается от перестановки 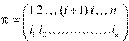, на одну инверсию, вследствие чего каждое слагаемое, входящее в определение определителя, поменяет знак. Стало быть, определитель матрицы, полученной перестановкой строк, тоже поменяет знак.

Если переставить не две соседние строки, а, скажем, i-ю и (i+k)-ю, то такую перестановку можно представить как последовательное смещение i-й строки на k строк вниз (при этом каждый раз знак определителя меняется), а (i+k)-ой строки на (k-1) вверх, что тоже сопровождается (k-1) изменением знака, то есть знак поменяется нечетное (2k-1) число раз. Следовательно, знак поменяется.

5) Если квадратная матрица содержит две одинаковые строки, то ее определитель равен 0.

Доказательство: действительно, поменяем одинаковые строки местами. С одной стороны значение определителя не изменилось, так как не изменилась матрица. С другой стороны по свойству (4) определитель должен был сменить знак. И то, и другое возможно одновременно, только если определитель равен нулю.

6) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен нулю.

Доказательство: пусть i-я строка равна k-ой, умноженной на . Тогда по свойству (2) этот общий множитель можно вынести за знак определителя. Полученный определитель, очевидно, содержит две одинаковые строки, и по свойству (5) равен нулю.

7) Прибавление кратного k-ой строке к i-ой строке не изменяет значение определителя

Доказательство: пусть к i-ой строке прибавили k-ую, умноженную на . Тогда определитель полученной матрицы примет вид:

Тогда используя последовательно свойство (3) и свойство (2), получим:

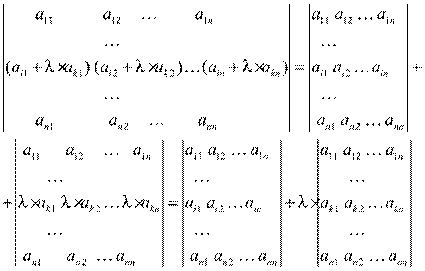
Первое из этих слагаемых есть определитель исходной матрицы, а второй определитель на i-м и k-м месте содержит k-ю строку и по свойству (5) равен нулю.

Это и означает, что:

 

Теорема: Разложение определителя по элементам строки:

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

, ()

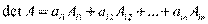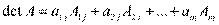Доказательство: Рассмотрим произвольный определитель n–го порядка:

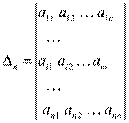
Каждый член определителя обязательно содержит в виде сомножителя только один из элементов его первой строки 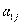(j = 1, 2, . . ., n). Следовательно, 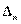можно представить в виде суммы: . Рассмотрим множитель 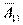при элементе 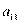. Очевидно, что он представляет собой алгебраическую сумму (n−1)! членов, каждый из которых является произведением (n−1) матричных элементов, взятых по одному из каждой строки и каждого столбца исходного определителя, за исключением первой строки и первого столбца, на пересечении которых располагается сам элемент .

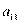Упорядочим матричные элементы в этих произведениях таким образом, чтобы их первые индексы располагались в порядке возрастания: 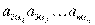. Поскольку второй индекс элемента 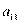(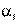=1) не образует инверсий в перестановке 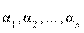, составленной из вторых индексов матричных элементов в каждом из содержащих исходного определителя 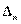, то очевидно, что знак каждого члена в выражении для 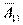определяется как 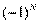, где N – число инверсий в перестановке 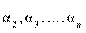из (n−1) номеров столбцов матричных элементов в произведении 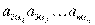, если при этом номера строк образуют возрастающую последовательность (n−1) чисел (2,3, . . .,n). Но тогда 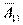представляет собой не что иное, как определитель (n−1)–го порядка, получающийся из исходного вычеркиванием 1–ой строки и 1–го столбца, т. е. минор матричного элемента : .

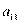Найдем теперь множитель 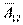при элементе . Для этого поменяем местами 1–ый и 2–й столбцы определителя 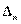. Тогда в преобразованном определителе элемент займет положение элемента 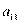исходного определителя.

Используя свойство (4), следствие свойства (1) и представление , получаем:

Повторяя рассуждения, приведенные ранее при определении 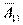, найдем, что . Пронося третий столбец исходного определителя на место второго, а затем и на место первого столбца, найдем, что .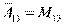

Продолжая этот процесс, нетрудно установить, что , если для того, чтобы разместить j–й столбец на месте 1–го, его необходимо последовательно переставить с четным числом 1,2,. . ., (j−1) столбцов, и - если с нечетным. В первом случае j должно быть нечетным числом, а во втором - четным. Следовательно, общее выражение для коэффициентов (j=1,2,. . .,n) разложения произвольного определителя n–го порядка по элементам 1–ой строки можно представить в форме: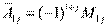

Для того, чтобы разложить определитель по элементам любой строки, достаточно переставить эту строку на место первой, учитывая, что при каждой перестановке строк определитель меняет знак на противоположный. Очевидно, что разложение определителя по элементам i–й строки будет иметь вид: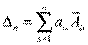, (i = 1,2, . . .,n) .

При этом коэффициенты разложения являются алгебраическими дополнениями

элементов определителя :.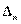

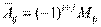Следствие: Сумма произведений элементов какой-либо строки определителя

n–го порядка на алгебраические дополнения элементов другой его строки равна

нулю, т. е. 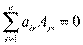при i, j =1,2, . . .,n и .

Доказательство: Рассмотрим определитель

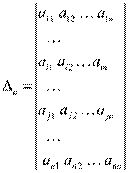и вспомогательный определитель: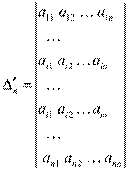

полученный из 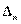заменой j–й строки на i–ю. По свойству (4) 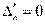как имеющий две одинаковые строки. С другой стороны, его можно вычислить, разлагая по элементам j–й строки. Используя Теорему о разложении определителя, находим:

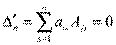при i, j =1,2, . . .,n и .

 

Теорема: Определитель произведения 2-х квадратных матриц порядка n равен произведению определителей этих матриц:

Доказательство: рассмотрим определитель произведения квадратных матриц A и B:

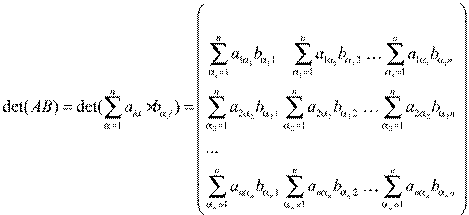
Применяя к каждой из строк полученного в правой части определителя свойство линейности определителей, получаем последовательно:

Заметим, что в правой части последнего соотношения достаточно учитывать лишь такие произведения , в которых все индексы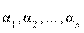различны. Действительно, при совпадении хотя бы двух индексов, определитель в правой части имеет две одинаковые строки и по свойству (5) равен нулю.

Таким образом, суммирование в правой части фактически проводится по всем возможным перестановкам 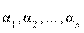чисел 1,2,. . ., n, а само выражение представляет собой сумму n! слагаемых, каждое из которых включает в себя произведение n элементов матрицы A, взятых по одному из каждой строки и каждого столбца.

Рассмотрим в сумме слагаемое, отвечающее расположению чисел 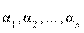в возрастающей последовательности 1,2,. . .,n, при которой перестановка 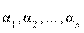не содержит инверсий. Очевидно, что в этом случае определитель в правой части является определителем матрицы B. Если какая-то пара чисел 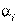и 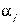(i, j = 1, 2, . . . , n) в перестановке 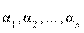образует инверсию, то поменяв местами в определителе в правой част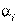и –ю и 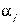–ю строки, мы получим определитель матрицы B, умноженный на 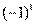. Если перестановка 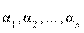содержит две инверсии, то очевидно, что дважды поменяв местами соответствующие строки определителя в правой части, мы получим определитель матрицы B, умноженный на .

Продолжая эти рассуждения и далее, нетрудно убедиться, что определитель в правой части равен , где N - число инверсий в перестановке .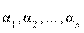

Вынося общий множитель |B| всех слагаемых за знак суммы, найдем:

где сумма берется по всем перестановкам 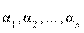. Но согласно определению данная сумма представляет собой не что иное, как определитель |A| матрицы A. Следовательно, det(AB) = detA · detB .

Обратная матрица.

Матрица А называется обратимой, если существует матрица В такая, что АВ=ВА=Е.

Обратимая матрица обязательно квадратная. Если А обратима, то есть только одна матрица В, удовлетворяющая условию АВ=ВА=Е (симметричный элемент), матрица B называется обратной к матрице А и обозначается .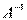

Матрицу называют невырожденной, если ее определитель , и вырожденной, если ее определитель =0.

 

Теорема: Критерий обратимость матрицы

Для того, чтобы матрица А имела обратную 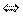, чтобы она была невырождена.

Доказательство:

Предположим, что матрица А обратима, тогда существует такая В, что АВ=ВА=Е. К равенству Е=АВ применяем теорему об определителе произведения матриц: .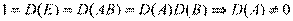

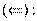
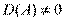. Суммируя результаты теоремы о разложении определителя, следствия из неё, а также учитывая принцип равноправия строк и столбцов, имеем:

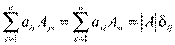(символ Кронекера ) при i, j =1,2, . . .,n.

Разделим каждую часть на |A| и введем в рассмотрение:

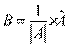
Матрицу n–го порядка 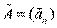с элементами , составленными из алгебраических дополнений 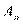матрицы A (i,j=1,2,. . .,n), в дальнейшем будем называть присоединенной. Ее явный вид:

С учетом обозначений имеем: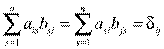

Или в матричной форме: АВ=ВА=Е

Сравнивая эти записи и принимая во внимание, что обратная матрица 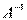, если она существует, является единственной, получаем, что 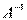= B. Теорема доказана.

Рассмотрим линейную систему:

Составим матрицу 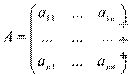- коэффициенты при неизвестных.

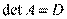Матрица А - квадратнаяимеет определитель . Теперь обозначим 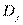- определитель матрицы, который получается из матрицы А заменой j-го столбца на столбец свободных членов:

Теорема(Правило Крамера): если матрица коэффициентов при неизвестных в СЛУ (n уравнений и n неизвестных) невырождена, то эта система совместная и определенная. Ее единственным решением является строчка: .

Доказательство: Докажем, что данная строчка является решением СЛУ.

Если решение существует, значит СЛУ совместна, подставим эту строчку в i-ое уравнение:

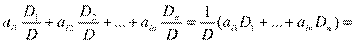
Разложим определитель по первому столбцу; определитель - по второму и т.д.

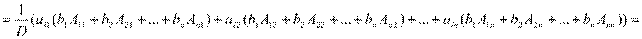
Группируем слагаемые, в которые входит 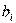, 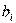выносим за скобки, аналогично

Коэффициент при 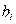равен 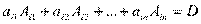; коэффициенты при остальных равны нулю. По формуле разложения определителя по строке:

- является решением СЛУ.

Докажем единственность решения. Берем любое решение 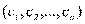и подставляем его в систему, получаем n тождеств:

…

Из этих тождеств следует, что столбец свободных членов является линейной комбинацией столбцов матрицы А: . Подставим в определитель 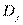эту линейную комбинацию. И применим свойство (2). Получим аналогичную линейную комбинацию n определителей, из которых (n-1) определитель имеет 2 равных столбца (j-ый столбец равен какому-то другому), поэтому обращается в ноль. А последний определитель, который не имеет одинаковых столбцов – есть определитель матрицы А, он равен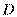 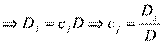- что доказывает единственность решения.

2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ (С.Л.У.)