Уравнение прямой на плоскости
| Th. 13.1 | Любая прямая на координатной плоскости может быть задана уравнением первой степени:
 (13.4)
И, наоборот, любое уравнение первой степени определяет на плоскости прямую. (13.4)
И, наоборот, любое уравнение первой степени определяет на плоскости прямую.
| |
Доказательство.
1) Положение прямой  однозначно определяется точкой однозначно определяется точкой 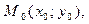 которая принадлежит прямой, и вектором которая принадлежит прямой, и вектором  Будем называть этот вектор нормальным вектором прямой или нормалью. Т.к Будем называть этот вектор нормальным вектором прямой или нормалью. Т.к 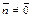 , то , то 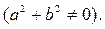 Выберем
Выберем  - текущую точку прямой - текущую точку прямой 
| 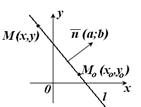 Рис. 13.1
Рис. 13.1
| |
Очевидно, что 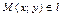 тогда и только тогда, когда
тогда и только тогда, когда  или
или  В координатной форме последнее равенство имеет вид:
В координатной форме последнее равенство имеет вид:
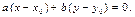 (13.5)
(13.5)
После раскрытия скобок получаем  , где
, где 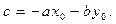 Таким образом, первая часть утверждения теоремы доказана.
Таким образом, первая часть утверждения теоремы доказана.
2) Пусть 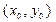 – одно из решений уравнения (13.4), т.е.
– одно из решений уравнения (13.4), т.е.
 (13.6)
(13.6)
Вычтем из уравнения (13.4) уравнение (13.6), получим 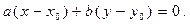 Это уравнение является координатной записью условия
Это уравнение является координатной записью условия 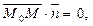 где
где 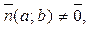
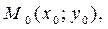
 Но это условие определяет прямую, которая проходит через точку М перпендикулярно вектору
Но это условие определяет прямую, которая проходит через точку М перпендикулярно вектору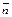 . Таким образом, доказано и второе утверждение теоремы .
. Таким образом, доказано и второе утверждение теоремы .