Уравнение плоскости в пространстве
Уравнению первой степени  на координатной плоскости соответствует в координатном простанстве уравнение
на координатной плоскости соответствует в координатном простанстве уравнение
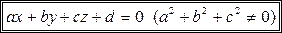 (14.1)
(14.1)
| Th. 14.1 | Каждое уравнение вида (14.1) определяет в пространстве плоскость наоборот, любая плоскость в координатном пространстве может быть задана уравнением (14.1) |
Доказательство этой теоремы полностью моделирует доказательство соответсвующего утверждения для прямой на плоскости (проведите его самостоятельно, используя рис. 14.1).
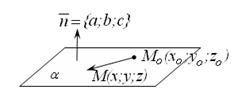 Рис. 14.1
Рис. 14.1
| 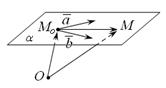 Рис. 14.2
Рис. 14.2
|
Уравнение (14.1) называется общим уравнением плоскости, вектор  – нормальным вектором плоскости.
– нормальным вектором плоскости.
Если плоскость проходит через точку 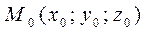 перпендикулярно вектору
перпендикулярно вектору 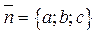 (рис. 14.1), то ее уравнение можно записать в виде:
(рис. 14.1), то ее уравнение можно записать в виде:
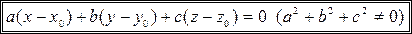 (14.2)
(14.2)
Плоскость  однозначно определяется точкой
однозначно определяется точкой  и двумя векторами
и двумя векторами  и
и  (
(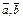 неколлинеарны). Векторы
неколлинеарны). Векторы  и
и  называются направляющими векторами плоскости. Пусть
называются направляющими векторами плоскости. Пусть  – текущая точка плоскости
– текущая точка плоскости 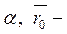 радиус вектор точки
радиус вектор точки 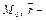 радиус-вектор точки
радиус-вектор точки 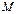 (рис. 14.2).
(рис. 14.2).
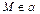 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 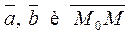 компланарны. А поскольку
компланарны. А поскольку 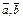 неколлинеарны, то
неколлинеарны, то  можно разложить по этим векторам, т.е. имеет место равенство:
можно разложить по этим векторам, т.е. имеет место равенство:

Учитывая, что 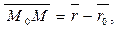 получаем:
получаем:
 (14.3)
(14.3)
Уравнение (14.3) называется векторным уравнением плоскости.
Т.к. 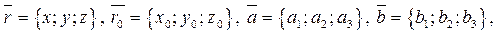 тоуравнение (14.3) в координатной форме принимает вид:
тоуравнение (14.3) в координатной форме принимает вид:
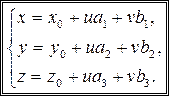 (14.4)
(14.4)
Уравнения (14.4) называются параметрическими уравнениями плоскости.
Условие компланарности векторов  можно выразить через смешанное произведение этих векторов:
можно выразить через смешанное произведение этих векторов:  , или в координатной форме:
, или в координатной форме:
 (14.5)
(14.5)
Уравнение (14.5) – уравнение плоскости, проходящей через точку  с заданными направляющими векторами
с заданными направляющими векторами 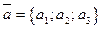 и
и 
Плоскость  однозначно определяется тремя точками
однозначно определяется тремя точками 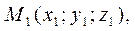
 не лежащими на одной прямой. В этом случае
не лежащими на одной прямой. В этом случае  и
и  – направляющие векторы плоскости
– направляющие векторы плоскости 
 Тогда из уравнения (14.5) получаем:
Тогда из уравнения (14.5) получаем:
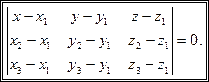 (14.6)
(14.6)
Уравнение (14.6) носит название уравнения плоскости, проходящей через три точки.
Пусть, в частности, известны точки, в которых плоскость  пересекает оси координат: пересекает оси координат: 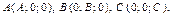 где где  (рис. 14.3) Тогда из уравнения (14.6) имеем: (рис. 14.3) Тогда из уравнения (14.6) имеем:
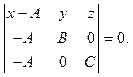
|  Рис. 14.3
Рис. 14.3
|
После раскрытия определителя получаем:
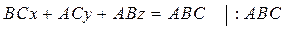
 (14.7)
(14.7)
Уравнение (14.7) называется уравнением плоскости в отрезках на осях.
5. Корни многочлена и их кратность. Теорема Безу. Схема Горнера.