Взаимное расположение прямой и плоскости

Угол между прямой и плоскостью.

Условие перпендикулярности прямой и плоскости.

Пусть плоскость a задана уравнением

 

Ах + Ву + Сz + D = 0,

а прямая l – уравнением

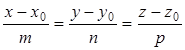
Углом между прямой и плоскостью является любой из двух смежных углов, образованных прямой и её проекцией на плоскости. Острый угол определяется из формулы

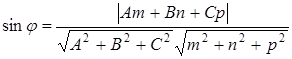
Плоскость и прямая взаимно перпендикулярны, если нормальный вектор плоскости коллинеарен направляющему вектору прямой, т.е.

 

Пересечение прямой и плоскости.

Условие принадлежности прямой к плоскости.

Пусть требуется найти точки пересечения прямой l с плоскостью a. Для этого надо решить систему, состоящую из уравнений плоскости a и прямой l. Проще всего это сделать, записав уравнение l в параметрическом виде:

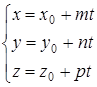
Подставляя эти выражения для x, y, z в уравнение плоскости, получим:

А(х₀ + mt) + B(y₀ + nt) + C(z₀ + pt) + D = 0,

откуда

t(Am + Bn + Cp) + (Aх₀ + By₀ + Cz₀ + D) = 0 (7)

Если прямая l не параллельна плоскости, т.е.

Am + Bn + Cp ≠ 0,

то из уравнения (7) находим значение t:

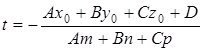
Подставляя значение в параметрическое уравнение прямой, найдем координаты точки пересечения прямой с плоскостью.

Рассмотрим случай, когда Am + Bn + Cp =0.

a) если F = Aх₀ + By₀ + Cz₀ + D ≠ 0, то l пересекать не будет плоскость a ввиду того, что t∙0 + F ≠ 0.

b) если Aх₀ + By₀ + Cz₀ + D = 0, то (7) имеет вид: t∙0 + 0 = 0. Любая точка прямой – точка пересечения прямой и плоскости, т.е. прямая лежит в плоскости. Таким образом, одновременное выполнение равенств

Aх₀ + By₀ + Cz₀ + D = 0 и Am + Bn + Cp =0

есть условие принадлежности прямой к плоскости.