рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- БУЛЕВА АЛГЕБРА
Реферат Курсовая Конспект
БУЛЕВА АЛГЕБРА
БУЛЕВА АЛГЕБРА - раздел Математика, Булева Алгебра В Этом Параграфе Будут Рассмотрены П...
БУЛЕВА АЛГЕБРА
В этом параграфе будут рассмотрены представления логических функций в виде суперпозиций функций И, ИЛИ, НЕ.
Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма. Введем обозначение х0 = 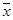 , х1 = х. Пусть
, х1 = х. Пусть — параметр, равный 0 или 1. Тогда
— параметр, равный 0 или 1. Тогда  = 1, если х =
= 1, если х =  и
и  = 0, если х
= 0, если х 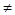 а.
а.
1 До сих пор все, что говорилось о формулах и суперпозициях, было справедливо не только для логических, но и для любых функций вообще (см. § 1-2). Данный же метод проверки эквивалентности годится только для функций о конечными областями определения.
Теорема 3-1. Всякая логическая функция f (х1, ..., хn) может быть представлена в следующем виде:
f(x1 , ..., xm , xm+1, ..., xn )= 
 f(
f(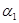 , ...,
, ...,  , xm+1, ..., xn ), (3–4)
, xm+1, ..., xn ), (3–4)
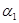 , ...,
, ..., 
где m  n, а дизъюнкция берется по всем 2m наборам значений переменных x1, ..., хm.
n, а дизъюнкция берется по всем 2m наборам значений переменных x1, ..., хm.
Это равенство называется разложением по переменным х1, ..., хm. Например, при n = 4, m = 2 разложение (3-4) имеет вид:
f(x1, x2, x3, x4) =  f(0, 0, x3, x4)
f(0, 0, x3, x4) 
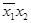 f&(0, 1, x3, x4)
f&(0, 1, x3, x4)

 f(1, 0, x3, x4 )
f(1, 0, x3, x4 ) 
 f(1, 1, x3, x4).
f(1, 1, x3, x4).
Теорема доказывается подстановкой в обе части равенства (3-4) произвольного набора ( , ...,
, ..., 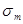 ,
,  , ...,
, ...,  ) всех n переменных. Так как
) всех n переменных. Так как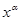 = 1 только когда х = а, то среди 2m конъюнкций
= 1 только когда х = а, то среди 2m конъюнкций  , ...,
, ...,  правой части (3-4) в 1 обратится только одна — та, в которой
правой части (3-4) в 1 обратится только одна — та, в которой 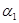 =
=  , ...,
, ...,  =
= 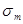 . Все остальные конъюнкции равны 0.
. Все остальные конъюнкции равны 0.
Поэтому получим: f( , ...,
, ...,  ) =
) = 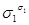 ...
... 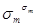 f(
f( , ...,
, ..., 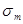 ,
,  , ...,
, ...,  )=f(
)=f( , ...,
, ...,  ),
),
т. е. тождество. D
При m =1 из (3-4) получаем разложение функции по одной переменной:
f(x1, x2, ..., xn) = 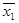 f(0, x2, ..., xn)
f(0, x2, ..., xn)  x1f(1, x2, ..., xn) (3-5)
x1f(1, x2, ..., xn) (3-5)
Ясно, что аналогичное разложение справедливо для любой из n переменных.
Другой важный случай — разложение по всем n переменным (m = n). При этом все переменные в правой части (3-4) получают фиксированные значения и функции в конъюнкциях правой части становятся равными 0 или 1, что дает:
f(x1, ..., xn) = 
 ...
...  , (3-6)
, (3-6)
f( , ...,
, ...,  )=1
)=1
где дизъюнкция берется по всем наборам ( , ...,
, ...,  ), на которых f = 1. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f.
), на которых f = 1. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции f.
СДНФ функции f содержит ровно столько дконъюнкций, сколько единиц в таблице f; каждому единичному набору ( , ...,
, ...,  ) соответствует конъюнкция всех переменных, в которой xi взято с отрицанием, если
) соответствует конъюнкция всех переменных, в которой xi взято с отрицанием, если 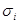 = 0, и без отрицания, если
= 0, и без отрицания, если  = 1. Таким образом, существует взаимнооднозначное соответствие между таблицей функции f (x1, ..., xn) и ее СДНФ и, следовательно, СДНФ для всякой логической функции единственна (как говорят в математике, “единственна с точностью до порядка конъюнкций”: это означает, что ввиду коммутативности дизъюнкции и конъюнкции — см. далее (3-8) — формулы, получаемые из (3-6) перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Например, функция, заданная табл. 3-1, имеет СДНФ
= 1. Таким образом, существует взаимнооднозначное соответствие между таблицей функции f (x1, ..., xn) и ее СДНФ и, следовательно, СДНФ для всякой логической функции единственна (как говорят в математике, “единственна с точностью до порядка конъюнкций”: это означает, что ввиду коммутативности дизъюнкции и конъюнкции — см. далее (3-8) — формулы, получаемые из (3-6) перестановкой конъюнкций и букв в конъюнкции, не различаются и считаются одной и той же СДНФ). Например, функция, заданная табл. 3-1, имеет СДНФ
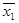

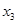



 .
.
Единственная функция, не имеющая СДНФ, — это константа 0.
Формулы, содержащие кроме - переменных (и, разумеется, скобок) только знаки функций дизъюнкции, конъюнкции и отрицания, будем называть булевыми формулами (напомним, что знак конъюнкции, как правило, опускается).
Соотношение (3-6) приводит к важной теореме.
Теорема 3-2. Всякая логическая функция может быть представлена булевой формулой, т. е. как суперпозиция конъюнкции, дизъюнкции и отрицания.
Действительно, для всякой функции, кроме константы 0, таким представлением может служить ее СДНФ. Константу 0 можно представить булевой формулой  [см. далее равенство (3-15)]. D
[см. далее равенство (3-15)]. D
Булева алгебра функций и эквивалентные преобразования в ней. Пусть функция f1 задана формулой F1 а функция f2 — формулой F2. Подстановка F1 и F2 в дизъюнкцию 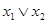 дает формулу
дает формулу  . Если взять формулу
. Если взять формулу 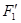 , эквивалентную F1 (т. е. тоже представляющую f1), и
, эквивалентную F1 (т. е. тоже представляющую f1), и  , эквивалентную f2, то получим формулу
, эквивалентную f2, то получим формулу  , эквивалентную
, эквивалентную  . (Доказательство эквивалентности можно провести стандартным методом (см. § 3-1); рекомендуем читателю его проделать). Таким образом, дизъюнкцию можно рассматривать как бинарную операцию на множестве логических функций, которая каждой паре функций f1, f2 независимо от вида формул, которыми они представлены, однозначно ставит в соответствие функцию
. (Доказательство эквивалентности можно провести стандартным методом (см. § 3-1); рекомендуем читателю его проделать). Таким образом, дизъюнкцию можно рассматривать как бинарную операцию на множестве логических функций, которая каждой паре функций f1, f2 независимо от вида формул, которыми они представлены, однозначно ставит в соответствие функцию 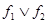 . Аналогично этому можно рассматривать конъюнкцию как бинарную операцию, а отрицание — как унарную операцию над функциями.
. Аналогично этому можно рассматривать конъюнкцию как бинарную операцию, а отрицание — как унарную операцию над функциями.
Алгебра (Р2;  , &,
, &,  ) основным множеством которой является все множество логических функций, а операциями — дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций. Операции булевой алгебры также часто называют булевыми операциями.
) основным множеством которой является все множество логических функций, а операциями — дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций. Операции булевой алгебры также часто называют булевыми операциями.
Фактически мы имеем дело, как правило, не с самими функциями в чистом виде, а с представляющими их формулами, т. е. с алгеброй формул, которых гораздо больше, чем функций, — ведь каждую функцию представляет бесконечное множество формул. Для того чтобы алгебра формул соответствовала алгебре функций, ей придается следующий вид. Элементами основного множества алгебры формул объявляются не формулы, а классы эквивалентности формул, т. е. классы формул, представляющих одну и ту же функцию. Результатом, например, дизъюнкции классов K1 и K2 считается класс всех формул, эквивалентных  , где
, где 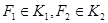 . Так определенная алгебра классов формул называется алгеброй Линденбаума—Тарского. Она изоморфна булевой алгебре функций. Этот изоморфизм настолько очевиден, что часто — особенно в прикладных работах — возникает смешение понятий формулы и функции. Следует ясно представлять себе, что, например, логическая схема на своем выходе реализует функцию от входов; когда же речь идет об эквивалентных преобразованиях, об упрощении и т. д., то имеются в виду преобразования формул, реализующих одну и ту же функцию.
. Так определенная алгебра классов формул называется алгеброй Линденбаума—Тарского. Она изоморфна булевой алгебре функций. Этот изоморфизм настолько очевиден, что часто — особенно в прикладных работах — возникает смешение понятий формулы и функции. Следует ясно представлять себе, что, например, логическая схема на своем выходе реализует функцию от входов; когда же речь идет об эквивалентных преобразованиях, об упрощении и т. д., то имеются в виду преобразования формул, реализующих одну и ту же функцию.
Рассмотрим теперь основные свойства булевых операций.
Ассоциативность:
a) x1(x2x3) = (x1x2)x3, б) (x1  x2)
x2)  x3 = x1
x3 = x1  (x2
(x2  x3). (3-7)
x3). (3-7)
Коммутативность:
a) x1x2 = x2x1; б) x1  x2 = x2
x2 = x2  x1. (3-8)
x1. (3-8)
Дистрибутивность конъюнкции относительно дизъюнкции:
x1(x2 x3) = x1x2
x3) = x1x2  x1x3 (3-9)
x1x3 (3-9)
Дистрибутивность дизъюнкции относительно конъюнкции:
x1  (x2x3) = (x1
(x2x3) = (x1  x2)(x1
x2)(x1  x3) (3-10)
x3) (3-10)
Идемпотентность:
а) хх = х; б) x  x = x. (3-11)
x = x. (3-11)
Двойное отрицание:
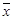 = x . (3-12)
= x . (3-12)
Свойства констант:
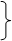 а) x & 1 = x; б) x & 0 = 0; в) x
а) x & 1 = x; б) x & 0 = 0; в) x  1 = 1;
1 = 1;  (3-13)
(3-13)
г) x  0 = x; д)
0 = x; д)  = 1; е)
= 1; е)  = 0.
= 0.
Правила де Моргана:
a) 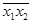 =
= 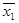

 ; б)
; б)  =
= 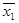
 . (3-14)
. (3-14)
Закон противоречия:
 = 0. (3-15)
= 0. (3-15)
Закон “исключенного третьего”:
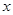

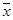 = 1. (3-16)
= 1. (3-16)
Соотношения (3-7) — (3-16) можно проверить указанным ранее стандартным методом — вычислением обеих частей равенств на всех наборах значений переменных. Ясно, что результат вычисления не зависит от того, как получены значения переменных, входящих в эти равенства, т. е. от того, являются ли эти переменные независимыми или, в свою очередь, получены в результате каких-то вычислений. Поэтому равенства (3-7) — (3-16) остаются справедливыми при подстановке вместо переменных любых логических функций и, следовательно, любых формул, представляющих эти функции. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной: при подстановке формулы F вместо переменной х все вхождения переменной х в исходное соотношение должны быть одновременно заменены формулой F. Например, соотношение  = 1 полученное из (3-16), верно для любых F, а соотношение
= 1 полученное из (3-16), верно для любых F, а соотношение  = 1 получено из (3-16) с нарушением правила подстановки и для некоторых F может оказаться неверным. Правило подстановки позволяет получать из соотношений (3-7) — (3-16) новые эквивалентные соотношения.
= 1 получено из (3-16) с нарушением правила подстановки и для некоторых F может оказаться неверным. Правило подстановки позволяет получать из соотношений (3-7) — (3-16) новые эквивалентные соотношения.
Зачем нужны эквивалентные соотношения? Во всякой алгебре (в том числе и в булевой алгебре функций) равенство F1 = F2 означает, что формулы F1 и F2 описывают один и тот же элемент алгебры, в данном случае одну и ту же логическую функцию f1. Следовательно, если какая-либо формула F содержит F1 в качестве подформулы, то замена F1 на F2 не изменяет элемента булевой алгебры f над которым производятся операции в формуле F; поэтому F', полученная из F такой заменой, эквивалентна F. Это утверждение представляет собой правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной.
Подчеркнем разницу между правилами подстановки и замены. При подстановке переменная заменяется на формулу; формула может быть любой, но требуется одновременная ее подстановка вместо всех вхождений переменной. При замене подформул может быть заменена любая подформула, однако не на любую другую, а только на эквивалентную ей. При этом замена всех вхождений исходной подформулы не обязательна. Пусть имеется эквивалентность F1 = F2, где F1 и F2 содержат переменную х. Если вместо всех вхождений х в F1 и F2 подставить произвольную формулу F, то получаются новые формулы 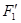 и
и  , причем не обязательно F1 =
, причем не обязательно F1 = 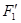 ,F2 =
,F2 =  ; однако между собой новые формулы будут эквивалентны:
; однако между собой новые формулы будут эквивалентны: 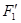 =
=  . Если же в F1 какую-либо подформулу заменить на эквивалентную ей, то получится новая формула
. Если же в F1 какую-либо подформулу заменить на эквивалентную ей, то получится новая формула 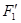 , эквивалентная F1.
, эквивалентная F1.
Пример 3-1. Возьмем первое из соотношений (3-14) и подставим  вместо x1. Получим
вместо x1. Получим 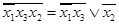 , т. е. две формулы, неэквивалентные исходным, но эквивалентные между собой. Если же в правой части нового соотношения
, т. е. две формулы, неэквивалентные исходным, но эквивалентные между собой. Если же в правой части нового соотношения  заменить формулой
заменить формулой 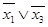 , эквивалентной ей в силу (3-14), а в полученной подформуле х1 заменить на эквивалентную ей в силу (3-12) формулу x1, то все формулы в построенной цепи преобразований
, эквивалентной ей в силу (3-14), а в полученной подформуле х1 заменить на эквивалентную ей в силу (3-12) формулу x1, то все формулы в построенной цепи преобразований  эквивалентны.
эквивалентны.
Такие преобразования, использующие эквивалентные соотношения (запас которых можно расширять с помощью правила подстановки) и правило замены, называются эквивалентными преобразованиями. Эквивалентные преобразования являются мощным средством доказательства эквивалентности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных.
Рассмотрим некоторые основные эквивалентные преобразования в булевой алгебре и новые соотношения, получаемые с их помощью из (3-7) — (3-16). При этом будем иметь в виду, что в булевой алгебре принято опускать скобки в следующих двух случаях: а) при последовательном выполнении нескольких конъюнкций или дизъюнкций (например, вместо (х1х2)x3 пишут х1х2x3 — это не вызывает неоднозначности ввиду ассоциативности этих операций (3-7); б) если они являются внешними скобками у конъюнкции: например, вместо (x1 (x2  x3))
x3))  (x4x5) пишут x1 (x2
(x4x5) пишут x1 (x2  x3)
x3)  x4x5. Оба соглашения совершенно аналогичны общепринятому опусканию скобок для умножения в арифметических формулах 1.
x4x5. Оба соглашения совершенно аналогичны общепринятому опусканию скобок для умножения в арифметических формулах 1.
1. Упрощение формул (т. е. получение эквивалентных формул, содержащих меньшее число символов).
а) Поглощение:
x  xy = x; (3-17а)
xy = x; (3-17а)
x (x  y) = x. (3-176)
y) = x. (3-176)
Докажем подробно первое равенство [для его доказательства используются последовательно соотношения (3-13а), (3-9), (3-1 Зв) и (3-1 За)]:
x  xy = x & 1
xy = x & 1  xy = x(1
xy = x(1  y) = x & 1 = x.
y) = x & 1 = x.
Второе равенство доказывается с помощью (3-9), (3-11) и первого равенства:
x(x  y) = xx
y) = xx  xy = x
xy = x  xy = x .
xy = x .
б) Склеивание:
xy 
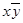 = x. (3-18)
= x. (3-18)
Доказательство: xy 
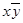 = x (y
= x (y 
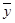 ) = x & 1 = x.
) = x & 1 = x.
в) Обобщенное склеивание:
xz 
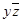
 xy = xz
xy = xz 
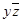 (3-19)
(3-19)
Доказывается с помощью расщепления, т. е. применения (3-18) в обратную сторону и поглощения (3-17): xz 
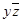
 xy = xz
xy = xz 
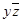
 xyz
xyz 
 = xz
= xz 
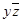 .
.
г) x 
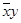 = x
= x  y. (3-20)
y. (3-20)
Доказательство: x 
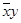 = xy
= xy 
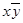

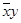
 xy
xy 
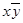
 xy
xy 
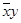 = x
= x  y.
y.
д) Обобщением равенств (3-17а) и (3-20) является равенство
x1  f(x1, x2, ..., xn) = x1
f(x1, x2, ..., xn) = x1  f(0, x2, ..., xn) (3-21)
f(0, x2, ..., xn) (3-21)
При доказательстве используется разложение по x1 , (3-17а) и (3-20):
x1  f(x1, x2, ..., xn) = x1
f(x1, x2, ..., xn) = x1 
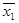 f(0, x2, ..., xn)
f(0, x2, ..., xn)  x1f(1, x2, ..., xn) = x1
x1f(1, x2, ..., xn) = x1  f(0, x2, ..., xn).
f(0, x2, ..., xn).
__________________
1 Внимательный читатель должен был обратить внимание на то, что эти два соглашения; а также соотношения (3-13) использованы уже в формуле (3-4).
2. Приведение к дизъюнктивной нормальной форме (в том числе к СДНФ).
Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций. Соотношение (3-19) показывает, что ДНФ функции может быть не единственной.
Приведение к ДНФ делается так. Сначала с помощью (3-12) и правил деМоргана (3-14) все отрицания “спускаются" до переменных. Затем раскрываются скобки, с помощью (3-11), (3-15) и (3-16) удаляются лишние конъюнкции и повторения переменных в конъюкциях, а с помощью (3-13)
удаляются константы.
Пример 3-2.
xy 
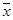 (y
(y  xz)
xz)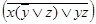 = xy
= xy 
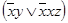
 = xy
= xy 
 = xy
= xy 

 = xy
= xy 
 =
= 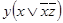 = xy
= xy 
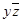 .
.
Всякую ДНФ можно привести к СДНФ расщеплением конъюнкций, которые содержат не все переменные, например:
xy 
 = xyz
= xyz 


 .
.
Если из формулы F1 с помощью некоторых эквивалентных соотношений можно получить формулу F2, то F2 можно получить из F1, используя те же эквивалентные соотношения; иначе говоря, всякое эквивалентное преобразование обратимо. Это позволяет доказать следующую теорему.
Теорема 3-3. Для любых двух эквивалентных формул F1 и F2 существует эквивалентное преобразование F1 в F2 с помощью соотношений (3-7) — (3-16).
Действительно, преобразуем F1 и F2 в СДНФ. Поскольку F1 и F2 эквивалентны, то их СДНФ совпадают. Обратив второе преобразование, получим преобразование F1 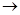 СДНФ
СДНФ 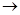 F2. D
F2. D
Важность этой теоремы в том, что соотношений (3-7) — (3-16) оказывается достаточно для любого эквивалентного преобразования в булевой алгебре.
3. Приведение к конъюнктивной нормальной форме.
Аналогично ДНФ определяется конъюнктивная нормальная форма (КНФ) как конъюнкция элементарных дизъюнкций.
От ДНФ к КНФ перейдем следующим образом. Пусть ДНФ F имеет вид 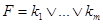 , где k1, ..., km — элементарные конъюнкции. Формулу
, где k1, ..., km — элементарные конъюнкции. Формулу  приведем к ДНФ
приведем к ДНФ  . Тогда
. Тогда  . По правилу де Моргана отрицания элементарных конъюнкций преобразуются в элементарные дизъюнкции, что и даст КНФ.
. По правилу де Моргана отрицания элементарных конъюнкций преобразуются в элементарные дизъюнкции, что и даст КНФ.
Пример 3-3.
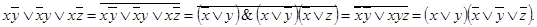 .
.
Аналогом СДНФ является СКНФ — совершенная конъюнктивная нормальная форма, каждая элементарная дизъюнкция которой содержит все переменные. Единственная функция, не имеющая СКНФ, — константа 1.
Двойственность. Функция f1 (x1, ..., хn) называется двойственной к функции f2 (х1, ..., хn), если f1 (x1, ..., xn) = f2(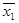 , ...,
, ...,  ). Беря отрицание над обеими частями равенства и подставляя
). Беря отрицание над обеими частями равенства и подставляя 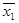 , ...,
, ...,  вместо x1, ..., хn получаем
вместо x1, ..., хn получаем  (
(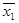 , ...,
, ...,  ) =
) =  (
( , ...,
, ..., 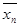 ) = f2 (x1, ..., xn), т. е. f2 двойственна к f1. Таким образом, отношение двойственности между функциями симметрично. Из определения двойственности ясно, что для любой функции двойственная функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
) = f2 (x1, ..., xn), т. е. f2 двойственна к f1. Таким образом, отношение двойственности между функциями симметрично. Из определения двойственности ясно, что для любой функции двойственная функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
Пример 3-4. Дизъюнкция двойственна конъюнкции (в силу правил де Моргана); константа 1 двойственна 0; отрицание самодвойственно. Еще один традиционный пример самодвойственной функции — ху  хz
хz  yz.
yz.
Пользуясь определением двойственности, нетрудно (прямой выкладкой) доказать следующее утверждение, называемое принципом двойственности: если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полу-ченнаяформула F* будетпредставлять функцию f*, двойственную f. В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из ранее приведенных примеров: если в формуле F, представляющей функцию f все конъюнкции заменить на дизъюнкции, дизъюнкции — на конъюнкции, 1 на 0, 0 на 1, то получим формулу F*, представляющую функцию f*, двойственную f.
Если функции равны, то и двойственные им функции также равны. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства F1 = F2 с помощью указанных замен к равенству F1* = F2*. Примером пары соотношений, получаемых друг из друга по принципу двойственности, являются два равенства (3-17).
Булева алгебра и теория множеств. В примере 2-1, п. 3 были описаны булевы алгебры множеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не случаен.
Всякая алгебра типа (2, 2, 1) называется булевой алгеброй, если ее операции удовлетворяют соотношениям (3-7) — (3-16). В алгебре множеств элементами являются подмножества фиксированного (“универсального”) множества U (напомним, что система всех подмножеств U обозначается через B(U)), операции & соответствует пересечение, операции  — объединение, операции
— объединение, операции  соответствует дополнение; единицей является само множество U, нулем — пустое множество. Справедливость соотношений (3-7) — (3-16) для алгебры множеств можно показать непосредственной их проверкой. Для этого нужно рассмотреть переменные в них как множества, знаки &,
соответствует дополнение; единицей является само множество U, нулем — пустое множество. Справедливость соотношений (3-7) — (3-16) для алгебры множеств можно показать непосредственной их проверкой. Для этого нужно рассмотреть переменные в них как множества, знаки &,  заменить на
заменить на 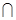 ,
, 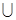 и показать, что если какой-либо элемент принадлежит множеству из левой части равенства, то он принадлежит правой части, и наоборот. Эту проверку мы предоставляем читателю.
и показать, что если какой-либо элемент принадлежит множеству из левой части равенства, то он принадлежит правой части, и наоборот. Эту проверку мы предоставляем читателю.
В предыдущих главах уже отмечалось и использовалось (см. теорему 1-2) взаимно-однозначное соответствие Г между множеством B(U), где U = {a1, ..., аn}, и множеством Вn двоичных векторов длины n: каждому подмножеству М 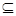 U соответствует двоичный вектор F (М) =
U соответствует двоичный вектор F (М) =  = (
= ( , ...,
, ...,  ), где
), где 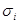 = 1, если ai
= 1, если ai  M, и
M, и 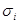 = 0, если ai
= 0, если ai 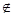 M. Булева алгебра (Вn;
M. Булева алгебра (Вn;  , &,
, &,  ) на множестве Вn определяется следующим образом: для любых векторов
) на множестве Вn определяется следующим образом: для любых векторов  = (
= ( , ...,
, ...,  ) и
) и 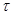 = (
= (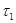 , ...,
, ...,  )
)


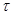 = (
= (

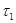 ,
,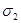

 , ...,
, ..., 

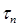 );
);
 &
& 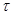 = (
= ( &
& 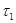 ,
,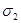 &
&  , ...,
, ...,  &
& 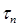 ); (3-22)
); (3-22)
 = (
= (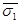 ,
, 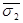 , ...,
, ...,  ).
).
Поскольку компоненты (разряды) 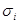 и
и  векторов
векторов  и
и 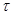 принимают значения 0 и 1, то указанные операции над компонентами — это просто логические операции над двоичными переменными; операции над векторами естественно назвать покомпонентными (поразрядными) логи
принимают значения 0 и 1, то указанные операции над компонентами — это просто логические операции над двоичными переменными; операции над векторами естественно назвать покомпонентными (поразрядными) логи
ческими операциями над двоичными векторами. Такие операции (наряду с логическими операциями над переменными) входят, в частности, в систему команд любой современной ЭВМ. Выполнение их очень просто: вектор 

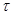 содержит единицы во всех разрядах, в которых есть 1 либо в
содержит единицы во всех разрядах, в которых есть 1 либо в  , либо в
, либо в 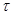 , вектор
, вектор  &
& 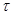 — в тех разрядах, в которых 1 есть и в
— в тех разрядах, в которых 1 есть и в  , и в
, и в 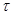 ; вектор
; вектор  содержит единицы в тех разрядах, в которых
содержит единицы в тех разрядах, в которых  содержит нули. Например, если
содержит нули. Например, если  = 01011,
= 01011, 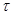 = 11010, то
= 11010, то 

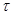 = 11011,
= 11011,  &
& 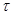 = 01010,
= 01010,  = 10100.
= 10100.
Теорема 3-4. Если |U| = n, то булева алгебра (B(U); 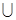 ,
, 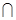 ,
,  ) изоморфна булевой алгебре (Bn;
) изоморфна булевой алгебре (Bn;  , &,
, &,  ).
).
Взаимно-однозначное соответствие Г между подмножествами U и векторами из Вn было описано ранее. Остается показать, что Г — изоморфизм, т. е. что для него выполнено условие (2-1), которое в данном случае сводится к трем равенствам: если Г (M1) =  , а Г (М2) =
, а Г (М2) = 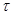 , то
, то
Г(M1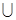 M2) =
M2) = 

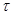 ;
;
Г(M1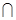 M2) =
M2) =  &
& 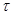 ; (3-23)
; (3-23)
Г(M1) =  .
.
Справедливость их вытекает непосредственно из (3-22): если ai  M1
M1 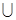 М2, то i-й разряд вектора Г (М1
М2, то i-й разряд вектора Г (М1 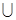 М2) = 1; с другой стороны, это означает, что ai
М2) = 1; с другой стороны, это означает, что ai  M1 или ai
M1 или ai  M2, т. е.
M2, т. е. 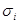 = 1 или
= 1 или  = 1 и, следовательно, i-й разряд вектора
= 1 и, следовательно, i-й разряд вектора 

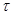 равен 1. Если же ai
равен 1. Если же ai 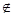 M1
M1 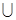 М2, то i-й разряд Г (M1
М2, то i-й разряд Г (M1 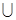 M2) равен 0. Но тогда ai
M2) равен 0. Но тогда ai 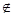 M1 и ai
M1 и ai 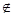 М2, следовательно, i-й разряд
М2, следовательно, i-й разряд 

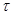 также равен 0. Аналогично доказываются остальные два равенства. D
также равен 0. Аналогично доказываются остальные два равенства. D
Эта теорема позволяет заменять теоретико-множественные операции (объединение, пересечение, дополнение) над системой подмножеств поразрядными логическими операциями над двоичными векторами. Такая замена очень часто используется при программировании, поскольку представление двоичных векторов и поразрядные операции над ними в ЭВМ реализуются очень просто.
Рассмотрим теперь множество Р2(m) всех логических функций m переменных х1, ..., хm. Оно замкнуто относительно операций &, ,
,  (результат их применения к функциям из P2(m) снова дает функцию из Р2 (m)) и, следовательно, образует конечную булеву алгебру (Р2(m);
(результат их применения к функциям из P2(m) снова дает функцию из Р2 (m)) и, следовательно, образует конечную булеву алгебру (Р2(m);  , &,
, &,  ), являющуюся подалгеброй булевой алгебры логических функций.
), являющуюся подалгеброй булевой алгебры логических функций.
Теорема 3-5. Если |U| = 2m, то булева алгебра множеств (B(U); 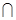 ,
, 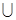 ,
,  ) изоморфна булевой алгебре функций (Р2(m);
) изоморфна булевой алгебре функций (Р2(m);  , &,
, &,  ).
).
Прежде всего отметим, что эти две алгебры равномощны и содержат 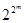 элементов. Кроме того, поскольку все множества U одинаковой мощности порождают изоморфные булевы алгебры множеств (см. пример 2-2, п. 5), то теорему достаточно доказать для какого-либо конкретного U, удовлетворяющего условию |U| = 2m. В качестве такого U возьмем множество Вm и, следовательно, будем доказывать изоморфизм между
элементов. Кроме того, поскольку все множества U одинаковой мощности порождают изоморфные булевы алгебры множеств (см. пример 2-2, п. 5), то теорему достаточно доказать для какого-либо конкретного U, удовлетворяющего условию |U| = 2m. В качестве такого U возьмем множество Вm и, следовательно, будем доказывать изоморфизм между
(B (Вm); 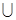 ,
, 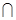 ,
,  ) и (Р2(m);
) и (Р2(m);  , &,
, &,  ).
).
Обозначим через Mf множество единичных наборов функции f; тогда набор  из Вm принадлежит Mf, если и только если f(
из Вm принадлежит Mf, если и только если f( ) = 1. Соответствие Г (f) = Mf между функциями и их единичными множествами является взаимно-однозначным соответствием между Р2(m) и B(Вm), поскольку различным функциям соответствуют различные множества, и наоборот. (Функцию f, единичным множеством которой служит М, называют характеристической функцией множества М.) Покажем, что Г является изоморфизмом. Для этого достаточно проверить услойие (2-1), которое в данном случае сводится к трем равенствам
) = 1. Соответствие Г (f) = Mf между функциями и их единичными множествами является взаимно-однозначным соответствием между Р2(m) и B(Вm), поскольку различным функциям соответствуют различные множества, и наоборот. (Функцию f, единичным множеством которой служит М, называют характеристической функцией множества М.) Покажем, что Г является изоморфизмом. Для этого достаточно проверить услойие (2-1), которое в данном случае сводится к трем равенствам
Г(f g) = Mf
g) = Mf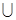 Mg;
Mg;
Г(f&g) = Mf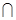 Mg;
Mg;
Г(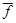 ) =
) = 
для любых функций f и g m переменных. Докажем первое из них. Пусть 
 Г (f
Г (f  g). Тогда f (
g). Тогда f ( )
) g (
g ( ) = 1, следовательно, f (
) = 1, следовательно, f ( ) = 1 или g (
) = 1 или g ( ) = 1 и, значит,
) = 1 и, значит, 
 Mf или
Mf или 
 Мg; откуда следует, что
Мg; откуда следует, что 
 (Mf
(Mf 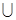 Mg). Обратный случай
Mg). Обратный случай 
 (Mf
(Mf 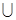 Mg). Тогда
Mg). Тогда 
 Mf или
Mf или 
 Мg и, следовательно, f (
Мg и, следовательно, f ( ) = 1 или g (
) = 1 или g ( ) = 1. Поэтому f (
) = 1. Поэтому f ( )
) g (
g ( ) = 1 и
) = 1 и 
 Г (f
Г (f  g). Аналогично доказываются и остальные два равенства. D
g). Аналогично доказываются и остальные два равенства. D
Замечание. Во избежание путаницы обращаем внимание читателя на различия объектов в доказанных нами теоремах.
1. В теореме 3-4 фигурировали алгебры со следующими основными множествами:
U ={a1, ..., аn} — множество произвольной природы и любой конечной мощности n;
B(U) — множество подмножеств U мощности 2n;
Вn — множество двоичных векторов длины n также мощности 2n.
В теореме 3-5 участвуют:
то же множество U, но с дополнительным условием n = 2m (m — любое натуральное число);
Вm — конкретное множество U с этим же условием: |Вm| = 2m;
множество Р2(m) логических функций m переменных;
|Р2(m)| = 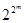 ;
;
B(Вm) — множество подмножеств Вm; |B(Вm)| = 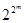 .
.
2. Множества Вn и Вm, хотя и имеют одну и ту же природу (состоят из двоичных наборов), использовались в теоремах 3-4 и 3-5 по-разному. В теореме 3-4 была использована структура элементов Вn, благодаря чему над ними оказались возможными поразрядные логические операции. Подмножества Вn не рассматривались. В теореме 3-5 структура элементов Вn не учитывалась, само Вn было выбрано только для естественности и наглядности, зато рассматривалась B(Вn) — система подмножеств Вn.
Теоремы 3-4 и 3-5 указывают на тесную связь между множествами и логическими функциями и позволяют переходить от операций над множествами к операциям над функциями и обратно. В частности, они дают возможность непосредственно производить операции над функциями, заданными не формулами, а таблицами или единичными множествами. Из теорем 3-4 и 3-5 следует, что булевы операции над функциями, заданными таблицами, сводятся к поразрядным логическим операциям над столбцами значений функций. Пример приведенв табл. 3-4, содержащей две функции f и g и результаты булевых операций над ними.
Таблица 3-4
| x1 | x2 | x3 | f | g | f g g
| fg | 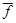
|
В завершение отметим еще один факт, связывающий логические функции с основными понятиями теории множеств: если (f 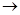 g)
g) 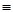 1, то Mf
1, то Mf 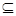 Mg. Действительно, если (f
Mg. Действительно, если (f 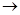 g)
g) 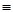 1, то из определения импликации (табл. 3-3, функция
1, то из определения импликации (табл. 3-3, функция 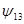 ) следует, что ни для какого набора
) следует, что ни для какого набора  не может быть одновременно f (
не может быть одновременно f ( ) = 1 и g (
) = 1 и g ( ) = 0, Поэтому если f (
) = 0, Поэтому если f ( ) = 1, то g (
) = 1, то g ( ) = 1, т. е. если
) = 1, т. е. если 
 Мf, то
Мf, то 
 Мg и, следовательно, Mf
Мg и, следовательно, Mf 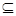 Mg. В таком случае говорят, что функция f имплицирует функцию g. При этом если f — элементарная конъюнкция, то f называется импликантом g, а если после удаления буквы f перестает быть импликантом g, то f называется простым импликантом g. Например, для функции х (у
Mg. В таком случае говорят, что функция f имплицирует функцию g. При этом если f — элементарная конъюнкция, то f называется импликантом g, а если после удаления буквы f перестает быть импликантом g, то f называется простым импликантом g. Например, для функции х (у  z) конъюнкции ху и хz — простые импликанты, а хуz — импликант, но не простой. Отметим, что любая конъюнкция любой ДНФ данной функции является импликантом этой функции.
z) конъюнкции ху и хz — простые импликанты, а хуz — импликант, но не простой. Отметим, что любая конъюнкция любой ДНФ данной функции является импликантом этой функции.
ДНФ, интервалы и покрытия. Теоретико-множественная интерпретация булевой алгебры функций оказывается очень удобным языком для изучения дизъюнктивных нормальных форм (ДНФ) и построения методов их упрощения. Рассмотрим кратко основные понятия, связанные с ДНФ.
Если функция f (x1, ..., хm) представляется элементарной конъюнкцией всех m переменных, то Mf содержит ровно один элемент множества Вm. Если же f — элементарная конъюнкция k переменных, где k < m, то Mf содержит 2m-k двоичных наборов (так как m — k переменных, не вошедших в эту конъюнкцию, несущественны для f и могут принимать любые 2m-k значений, не изменяя f). Множество Mf такой функции f называется интервалом. Например, для m = 4 и f(x1, х2, х3, x4) = x2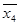 Mf = {0100, 0110, 1100, 1110} и |Mf| = 22 = 4. В этом случае говорят, что конъюнкция x2
Mf = {0100, 0110, 1100, 1110} и |Mf| = 22 = 4. В этом случае говорят, что конъюнкция x2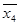 (точнее, интервал
(точнее, интервал 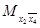 покрывает множество Mf (и все его подмножества). Представление f в виде ДНФ соответствует представлению ее единичного множества в виде объеди-
покрывает множество Mf (и все его подмножества). Представление f в виде ДНФ соответствует представлению ее единичного множества в виде объеди-
Таблица 3-5
| xz | ||||
y
| ||||
| xy |
нения интервалов; в совокупности все конъюнкции ДНФ покрывают все единичное множество f. Верно и обратное: если все элементы некоторого интервала Мk, принадлежат Mf, то существует ДНФ функции f, содержащая конъюнкцию k. В частности, СДНФ функции f соответствует просто перечислению элементов Mf. Отношение покрытия между конъюнкциями ДНФ и элементами Mf наглядно задается таблицей покрытия, строки которой соответствуют конъюнкциям (т. е. интервалам), столбцы — элементам Mf, а на пересечении строки i со столбцом j стоит какая-либо отметка (например, 1), если i-я конъюнкция покрывает j-й элемент Mf. Например, ДНФ F = хz / y / ху соответствует таблица покрытия (табл. 3-5).
/ ху соответствует таблица покрытия (табл. 3-5).
Из табл. 3-5 видно, что интервал Мху покрывается объединением интервалов Мхz и Мy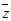 . Поэтому исключение ху из F не изменит единичного множества данной функции и получится теоретико-множественное доказательство соотношения (3-19). Еще более очевидное обоснование имеет закон поглощения х / ху = х: интервал Мху всегда покрывается интервалом Мх. Этот закон в терминах ДНФ можно переформулировать следующим образом: любой импликант k ДНФ, не являющийся простым, можно заменить простым импликантом k0, покрывающим k; импликант k0 получается из k вычеркиванием некоторых букв.
. Поэтому исключение ху из F не изменит единичного множества данной функции и получится теоретико-множественное доказательство соотношения (3-19). Еще более очевидное обоснование имеет закон поглощения х / ху = х: интервал Мху всегда покрывается интервалом Мх. Этот закон в терминах ДНФ можно переформулировать следующим образом: любой импликант k ДНФ, не являющийся простым, можно заменить простым импликантом k0, покрывающим k; импликант k0 получается из k вычеркиванием некоторых букв.
Таким образом, для любой функции f существует ДНФ F, состоящая только из простых импликантов. Ясно, что ДНФ F / k, где k — простой импликант f, не содержащийся в F, также представляет f. Поэтому дизъюнкция всех простых импликантов f, называемая сокращенной ДНФ, также будет представлять f.
Методы упрощения ДНФ (а их в настоящее время известно довольно много) состоят, как правило, из двух этапов. На первом этапе получают список всех простых импликантов, т. е. сокращенную ДНФ. Это можно сделать, например, при помощи эквивалентных преобразований. На втором этапе, используя таблицу покрытия (или аналогичные методы), удаляют “лишние” импликанты, покрываемые другими импликантами. ДНФ, из которой нельзя удалить ни одного импликанта, называется тупиковой.
– Конец работы –
Используемые теги: Булева, Алгебра0.058
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: БУЛЕВА АЛГЕБРА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов