рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Решение систем линейных уравнений в EXCEL

Реферат Курсовая Конспект

Выберите учебное заведение

Решение систем линейных уравнений в EXCEL

Решение систем линейных уравнений в EXCEL - раздел Математика, ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Сначала Рассмотрим Решение Системы Линейных Уравнений ...

Сначала рассмотрим решение системы линейных уравнений методом Крамера. Для этого используем уже решенный пример 11.

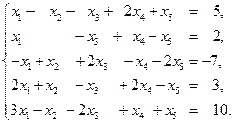
В EXCEL реализована функция вычисления определителей (см. п.7). Запишем матрицу коэффициентов и матрицы, полученные из нее заменой по очереди всех столбцов на столбец свободных членов. Листинг вычислений представлен на рис. 8:

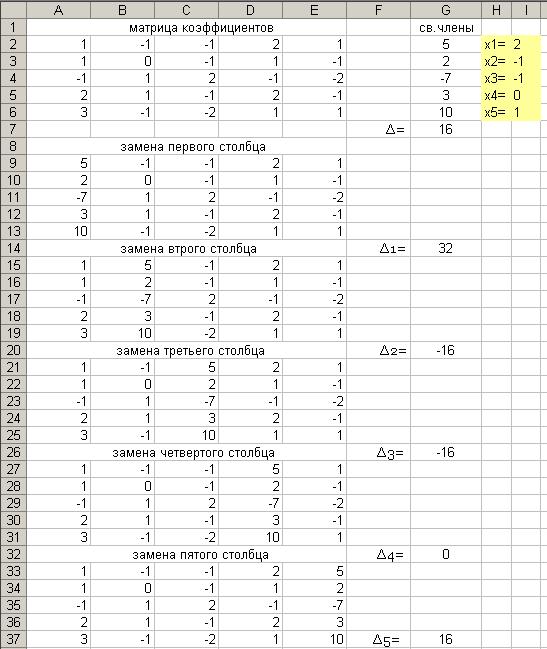
Рис. 8

Матрицы записаны в диапазонах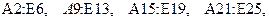

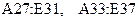, а значения определителей – в ячейках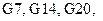 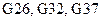. Столбец свободных членов – в G2:G6. Решение системы – в I2:I6.

Тот же пример решим с помощью обратной матрицы. В EXCEL реализованы функции для нахождения обратных матриц и перемножения матриц (см. п.7). Листинг решения представлен на рис. 9. В диапазоне 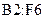записана матрица коэффициентов, в ячейках 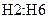– вектор свободных членов, в диапазоне 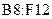обратная матрица, в ячейках 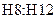– решение системы, полеченное как результат умножения матрицы 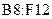на матрицу .

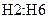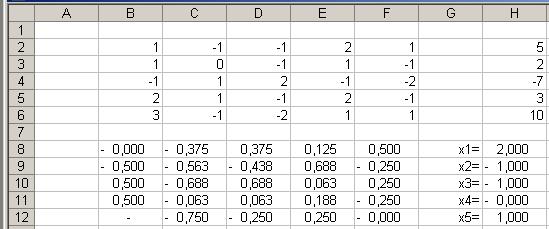
Рис. 9

Предложим еще один способ решения линейных систем в EXCELL. Возможно, для систем он не покажется эффективным, однако знакомство с ним полезно для решения задач оптимизации, в частности задач линейного программирования. Инструментом для этого метода служит процедура Поиск решения,которая находится в Надстройках. После вызова процедуры появляется окно, представленное на рис. 11.

Покажем решение системы на примере.

►Пример 18.Решить систему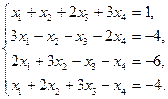

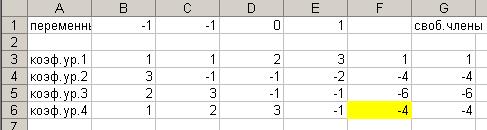
Рис. 10

В ячейки 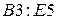введена матрица коэффициентов 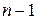уравнений системы, в 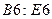– коэффициенты последнего уравнения, в ячейки G3:G6 - столбец свободных членов. Ячейки B1:E1 отведем для значений неизвестных. В ячейках F3:F6 сосчитаем сумму произведений коэффициентов каждого уравнения на неизвестные (для этого воспользуемся встроенной функцией СУММПРОИЗВ). Выберем ячейку F6 в качестве целевой и вызовем процедуру Поиск решения. В окошке установим, что целевая ячейка должна быть равной свободному члену последнего уравнения, и заполним поля. В поле «изменяя ячейки» введем B1:E1. В поле «ограничения» будем вводить первые 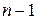уравнения. А именно, значение в ячейке F3 должно равняться заданному значению в ячейке G3 (1-е уравнение). Аналогично добавляем два других уравнения. После заполнения всех полей нажимаем .

Решение системы находится в ячейках B1:E1.

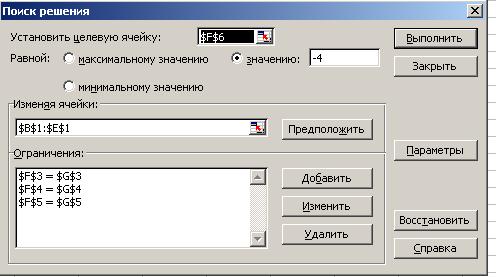
Рис. 11

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ... Введение...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение систем линейных уравнений в EXCEL

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Матрицы и действия с матрицами
Матрицей размера называется прямоугольная таблица чисел, содержащая

Упражнения.
1. Даны матрицы: Выполнить действия: а)

Определители
Определителем (детерминантом) n-го порядка называется числовая характеристика квадратной матрицы A размера

Свойства определителей.
Так как определитель не меняется при транспонировании матрицы, свойства, приведенные ниже для строк, справедливы и для столбцов. 1. Определитель, имеющий нулевую строку равен нулю.

Упражнения.
1. Вычислить определители: а) ; б)

Обратная матрица. Решение матричных уравнений
Матрица называется обратной к квадратной матрице

Упражнения.
1. Для заданных матриц найти обратную матрицу: а) ; б)

Ранг матрицы
Рангом матрицы (обозначение:

Теорема Крамера.
Пусть дана система, в которой число уравнений совпадает с числом неизвестных (10) Е

Упражнения.
Решить системы по формулам Крамера: 1) 2)

Решение систем с помощью обратной матрицы
Система из уравнений с

Упражнения.
Найти решение систем с помощью обратной матрицы: а) б)

Теорема Кронекера-Капелли.
Для совместности системы линейных уравнений необходимо и достаточно, чтобы ранг ее основной матрицы (

Упражнения.
Исследовать и решить системы уравнений: 1. Ответ:

Однородные системы
Система однородных уравнений всегда совместна. Если ранг матрицы коэффициентов равен числу неизвестных, то система имеет единственное нулевое (тривиальное) решение.

Упражнения.
Решить системы: 1) 2)

Собственные значения и собственные векторы матрицы
Комплексное число называется собственным числом квадратной матрицы

Упражнения.
Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц: 1)

Действия с матрицами на компьютере в EXCEL
Рассмотрим применение табличного процессора EXCEL для работы с матрицами. Процессор EXCEL работает с числовыми матрицами и может осуществлять следующие опер

Сложение матриц.
Рис.3 В ячейки

Умножение матрицы на число.
Рис.4 В ячейки

Вычисление определителя, транспонирование, нахождение обратной матрицы.
Перечисленные операции проводятся с помощью соответствующих встроенных функций. При выполнении операций транспонирования, умножения матриц, нахождения обратной матрицы необходимо предварите

Вычисление ранга матрицы.
Будем последовательно получать нули в первом, втором и т.д. столбцах ниже диагональных элементов.

Ввод матрицы.
In[4]:= m1 = {{2, -5, 4}, {3, -1, 8}, {2, 6, 1}, {-1, 3, 4}} Out[4]= {{2, -5, 4}, {3, -1, 8}, {2, 6, 1}, {-1, 3, 4}} Имя матрицы m1. Сама матрица вводится построчно с использование фиг

Определение ранга матрицы.
In[18]:= MatrixRank[m1] Out[18]= 3 Решение систем линейных уравнений. In[17]:= Solve[{2 x + y - z + 2 t == 12, -x + 2 y + 4 z + 3 t == 4, 2 x + y + 4 z -