рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Свойства определителей.
Реферат Курсовая Конспект
Свойства определителей.
Свойства определителей. - раздел Математика, ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Так Как Определитель Не Меняется При Транспонировании Матрицы, Свойства, Прив...
Так как определитель не меняется при транспонировании матрицы, свойства, приведенные ниже для строк, справедливы и для столбцов.
1. Определитель, имеющий нулевую строку равен нулю.
2. Определитель, у которого две строки равны или пропорциональны, равен нулю.
3. Общий множитель строки можно выносить за знак определителя.
4. Перестановка двух строк определителя изменяет знак определителя.
5. Если строку определителя умножить на постоянное число и прибавить к другой строке, то определитель не изменится.
6. Сумма произведений элементов строки на соответствующие алгебраические дополнения к элементам другой строки равна нулю.
7. Определитель можно представить в виде суммы определителей согласно формуле
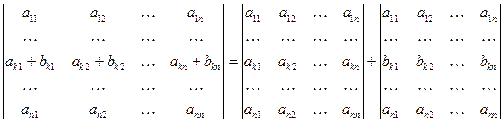 .
.
8. Определитель 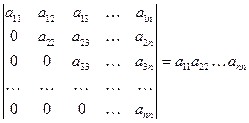 .
.
То есть определитель треугольной матрицы равен произведению ее диагональных элементов.
9. Определитель произведения квадратных матриц равен произведению определителей этих матриц:  .
.
►Пример 2. Вычислить определители:
1) ,2)
,2)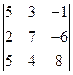 ,3)
,3) , 4)
, 4) 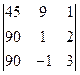 , 5)
, 5) 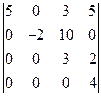 ,
,
6) 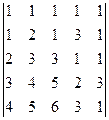 , 7)
, 7)  .
.
Решение.
1) Определитель вычислим по формуле (1) 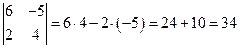 .
.
2) Определитель вычислим по формуле (2) и по формулам (3,4) . По формуле (2)
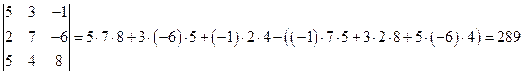 .
.
Для вычисления по формуле (3) возьмем вторую строку (выбор строки произволен) и вычислим миноры и алгебраические дополнения к элементам этой строки
 .
.
 .
.
По формуле (3) имеем 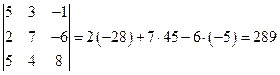 .
.
3) Заметим, что в определителе  во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец
во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец
 .
.
4) Заметим, что первый столбец определителя 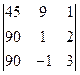 имеет общий множитель. Вынесем этот множитель за знак определителя
имеет общий множитель. Вынесем этот множитель за знак определителя
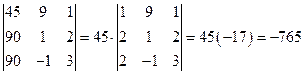 .
.
5) Определитель 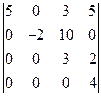 имеет треугольный вид, следовательно,
имеет треугольный вид, следовательно,
 .
.
6) Определитель 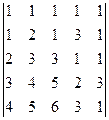 имеет пятый порядок. Разложение по элементам строки (столбца) приводит к четырем определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем
имеет пятый порядок. Разложение по элементам строки (столбца) приводит к четырем определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем
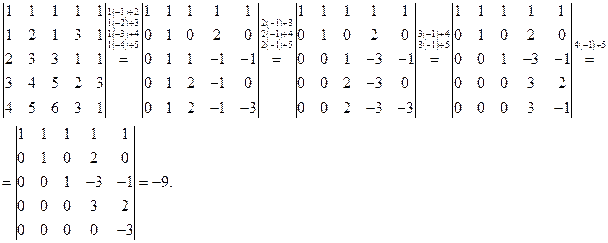
7) Воспользуемся формулой (3), а определители третьего порядка вычислим по схеме Саррюса:
 . ◄
. ◄
►Пример 3. Решить уравнение 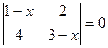 .
.
Решение.
По формуле (1) раскроем определитель, а затем решим уравнение
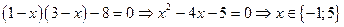 . ◄
. ◄
►Пример 4. Найти определитель  .
.
Решение.
Все столбцы, начиная со второго, прибавим к первому столбцу, вынесем общий множитель из вновь полученного первого столбца, а затем первую строку вычтем из всех остальных

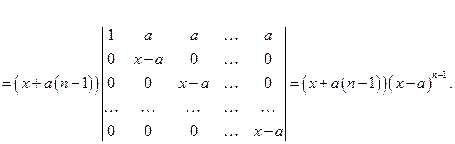 ◄
◄
– Конец работы –
Эта тема принадлежит разделу:
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ... Введение...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства определителей.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов