Векторное произведение векторов
Векторным произведением двух векторов 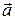 и
и  называется вектор
называется вектор  , обозначаемый
, обозначаемый 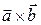 , который удовлетворяет следующим условиям:
, который удовлетворяет следующим условиям:
1) вектор  перпендикулярен плоскости, в которой лежат векторы
перпендикулярен плоскости, в которой лежат векторы 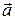 и
и  ;
;
2) вектор  имеет длину, численно равную площади параллелограмма, построенного на векторах
имеет длину, численно равную площади параллелограмма, построенного на векторах 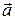 и
и  как на сторонах:
как на сторонах:
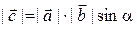 , где α – угол между векторами
, где α – угол между векторами 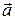 и
и  ;
;
3) векторы 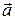 ,
,  ,
,  образуют правую тройку.
образуют правую тройку.
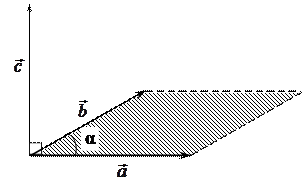 |
Рис. 17
 Три произвольных некомпланарных вектора
Три произвольных некомпланарных вектора 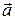 ,
,  ,
,  , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора  кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 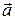 ко второму вектору
ко второму вектору  виден совершающимся против часовой стрелки (рис. 18), и левую, если по часовой стрелке.
виден совершающимся против часовой стрелки (рис. 18), и левую, если по часовой стрелке.
Рис. 18
Если система координатных осей правая и векторы 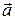 и
и  заданы своими координатами,
заданы своими координатами, 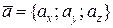 ,
,  , то векторное произведение
, то векторное произведение 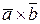 определяется по формуле:
определяется по формуле:
 .
.
Площадь параллелограмма S, построенного на векторах 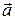 и
и  , равна модулю векторного произведения
, равна модулю векторного произведения 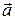 ×
×  и определяется по формуле:
и определяется по формуле:
S = | |.
|.
Площадь треугольника SD, построенного на векторах 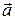 и
и  , равна половине площади параллелограмма:
, равна половине площади параллелограмма:
SΔ = 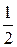 S =
S = 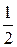 |
| |.
|.