Прямая и плоскость в пространстве
Угол между плоскостью Ах + Ву + Сz + D = 0 и прямой, заданной каноническими уравнениями 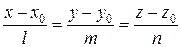 , определяется по формуле:
, определяется по формуле:
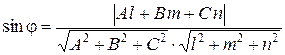 .
.
Прямая и плоскость параллельны, если Al + Bm + Cn = 0.
Прямая и плоскость перпендикулярны, если 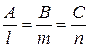 .
.
Прямая, проходящая через точку М(х0; у0; z0) и перпендикулярная к плоскости Ах + Ву + Сz + D = 0, имеет направляющий вектор 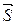 (А; В; С) и определяется уравнениями:
(А; В; С) и определяется уравнениями:
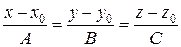 .
.
Расстояние от точки М1(х1; у1; z1) до прямой 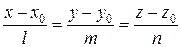 , определяется по формуле:
, определяется по формуле:
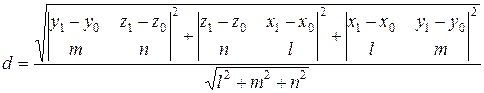 .
.
Пример 7.Даны координаты четырех точек А(1; –1; 1), В(–2; 1; 3), С(4; –5; –2), D(–1; 1; –2). Необходимо найти:
1) уравнение плоскости Q, проходящей через точки А, В, С;
2) канонические уравнения прямой АВ;
3) уравнение плоскости G, проходящей через точку D перпендикулярно прямой АВ;
4) расстояние от точки D до плоскости Q.
Решение.
Уравнение плоскости, проходящей через три данные точки М1 (х1; у1; z1), М2 (х2; у2; z2), М3 (х3; у3; z3), имеет вид:
 .
.
Составим уравнение плоскости Q, проходящей через точки А, В, С:
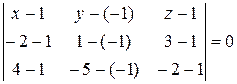 .
.
Преобразуем уравнение плоскости, разложив определитель по первой строке:
 ; (х – 1)
; (х – 1)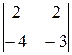 – (у + 1)
– (у + 1)  + (z – 1)
+ (z – 1)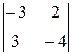 = 0;
= 0;
2(х – 1) –3(у + 1) + 6(z – 1) = 0.
Тогда уравнение плоскости Q имеет вид: 2х – 3у + 6z – 11 = 0.
2. Уравнения прямой, проходящей через две данные точки А1 (х1; у1; z1), А2 (х2; у2; z2), определяется по формуле:
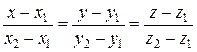 .
.
Подставляя координаты точек А(1; –1; 1) и В(–2; 1; 3), получим канонические уравнения прямой АВ:
 или
или  .
.
Направляющий вектор прямой АВ имеет координаты 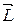 (–3; 2; –3).
(–3; 2; –3).
3. Так как искомая плоскость G перпендикулярна прямой АВ, то вектор нормали плоскости  параллелен направляющему вектору прямой АВ
параллелен направляющему вектору прямой АВ  , т.е.
, т.е. 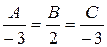 .
.
Уравнение плоскости, проходящей через точку М(х0; у0; z0) перпендикулярно вектору нормали  , имеет вид:
, имеет вид:
А(х – х0) + В(у – у0) + С(z – z0) = 0.
Подставляя в это уравнение вместо коэффициентов А, В, С пропорциональные им числа –3; 2; –3 и координаты точки D (–1; 1; –2), получим уравнение плоскости, перпендикулярной прямой АВ:
–3(х – (–1)) + 2(у – 1) + (–3)(z – (–2)) = 0.
Преобразуем данное уравнение:
–3(х + 1) + 2(у – 1) –3(z + 2) = 0; –3х + 2у – 3z – 11 = 0 (плоскость G).
4. Расстояние от точки М(х0; у0; z0) до плоскости Q Ах + Ву + С + D = 0 определяется по формуле:
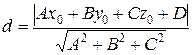 .
.
Подставляя координаты точки D (–1; 1; –2) и коэффициенты общего уравнения плоскости Q 2х –3у + 6z – 11 = 0, найдем расстояние от точки до плоскости:
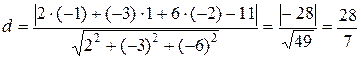 = 4.
= 4.
4.4. Вопросы для самоконтроля
1. Напишите общее уравнение плоскости.
2. Напишите неполные уравнения плоскости.
3. Какой вектор называется нормальным к плоскости?
4. Напишите уравнение плоскости, проходящей через данную точку перпендикулярно нормальному вектору.
5. Какой вид имеет уравнение плоскости, проходящей через три данные точки?
6. Напишите уравнение плоскости в отрезках на координатных осях.
7. Напишите формулу для определения угла между двумя плоскостями.
8. Напишите условия параллельности и перпендикулярности двух плоскостей.
9. Напишите уравнение плоскости, проходящей через данную точку параллельно данной плоскости.
10. Как найти расстояние от точки до плоскости?
11. Напишите общие уравнения прямой.
12. Какой вектор называется направляющим для прямой?
13. Напишите канонические уравнения прямой.
14. Напишите параметрические уравнения прямой.
15. Какой вид имеет уравнение прямой, проходящей через две данные точки?
16. Как найти угол между прямой и плоскостью?
17. Напишите условия параллельности и перпендикулярности прямой и плоскости.
18. Напишите уравнение прямой, проходящей через данную точку перпендикулярно к данной плоскости.
19. Как найти расстояние от точки до прямой в пространстве?