Метод обратной матрицы

Пусть число уравнений системы равно числу переменных: т = п.Тогда матрица системы является квадратной. Ее определитель D(А) называется определителем системы.

Для получения решения системы линейных уравнений при т = п в общем виде предположим, что квадратная матрица системы А невырожденная: ее определитель D(А) ≠ 0. В этом случае существует обратная матрица А^-1.

Умножим обе части матричного равенства А Х = В на матрицу А^-1 слева. В результате получим такие соотношения:

А^–1 (АХ) = А^–1В;

А^–1 (АХ) = (А^–1А) Х = ЕХ = Х.

Следовательно, решением системы линейных уравнений методом обратной матрицы является матрица-столбец, равная произведению обратной матрицы А^-1 и матрицы свободных членов В:

Х = А^–1 В.

Отыскание решения системы по данной формуле называют матричным методом решения системы.

Пример 1. Решить систему линейных уравнений матричным методом

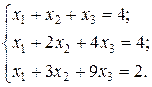
Решение.

Обозначим: А – матрица коэффициентов при переменных; Х – матрица-столбец переменных х₁, х₂, х₃; В – матрица-столбец свободных членов:

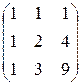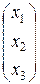А = , Х = , В = .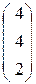

Исходную систему уравнений запишем в матричном виде:

А · Х = В.

Решение системы будем искать в виде:

Х = А^–1 ·В.

Вычислим определитель матрицы А:

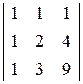∆ = = 18 + 3 + 4 – 2 – 12 – 9 = 2 ¹ 0.

Так как ∆ ¹ 0, то матрица А имеет обратную матрицу А^–1.

Найдем транспонированную матрицу А^Т:

А^Т = .

Вычислим союзную матрицу А_с, составленную из алгебраических дополнений A_ij элементов матрицы А^Т:

А_с = = .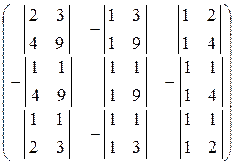

Запишем обратную матрицу А^–1:

А^–1 = = .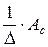

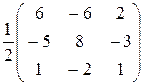Найдем решение системы линейных уравнений в матричной форме:

Х = А^–1 · В = ∙ =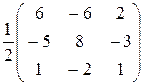

= .

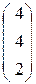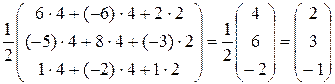Отсюда х₁ = 2, х₂ = 3, х₃ = –1.