Гипербола
Гиперболойназывается геометрическое место точек, для которых разность расстояний от двух фиксированных точек, называемых фокусами, есть величина постоянная, равная 2а.
Каноническое (простейшее) уравнение гиперболы имеет вид:
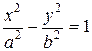 .
.
Гипербола, заданная каноническим уравнением, симметрична относительно осей координат, центр её симметрии находится в начале координат (рис. 10). Параметр а называют действительной полуосью, параметр b – мнимой полуосью гиперболы. Гипербола пересекает ось Ох в двух точках. Эти точки называются вершинами гиперболы.
Фокусы F1 и F2 находятся на оси Оx на расстоянии 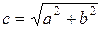 от центра и имеют координаты F1(– c; 0) и F2 (c; 0).
от центра и имеют координаты F1(– c; 0) и F2 (c; 0).
Отношение 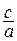 = e > 1 называется эксцентриситетом гиперболы.
= e > 1 называется эксцентриситетом гиперболы.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называют основным прямоугольником гиперболы. Диагонали основного прямоугольника гиперболы совпадают с её асимптотами.
Асимптоты гиперболы определяются уравнениями: 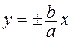 .
.
Расстояния произвольной точки М(x; y) гиперболы от его фокусов F1М и F2М (фокальные радиус-векторы r1 и r2) определяются формулами:
для точек правой ветви гиперболы
r1 = eх + а, r2 = eх – а;
для точек левой ветви гиперболы
r1 = – (eх + а); r2 = – (eх – а).
Прямые х = – 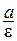 и х =
и х = 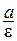 называются директрисами гиперболы. Каждая директриса обладает следующим свойством: если r – расстояние произвольной точки гиперболы до некоторого фокуса, d – расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение
называются директрисами гиперболы. Каждая директриса обладает следующим свойством: если r – расстояние произвольной точки гиперболы до некоторого фокуса, d – расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение 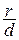 есть величина постоянная, равная эксцентриситету гиперболы e.
есть величина постоянная, равная эксцентриситету гиперболы e.
Каноническое уравнение 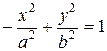 определяет гиперболу, симметричную относительно осей координат с фокусами F1 и F2 на оси Оу. Фокусы находятся на расстоянии
определяет гиперболу, симметричную относительно осей координат с фокусами F1 и F2 на оси Оу. Фокусы находятся на расстоянии 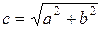 от центра и имеют координаты F1(0; – с) и F2(0; с). Эксцентриситет гиперболы определяется соотношением e =
от центра и имеют координаты F1(0; – с) и F2(0; с). Эксцентриситет гиперболы определяется соотношением e = 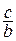 ; директрисы имеют уравнения у = –
; директрисы имеют уравнения у = – 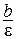 и у =
и у = 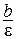 .
.
Гиперболы 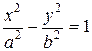 и
и 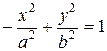 называются сопряженными.
называются сопряженными.
Гипербола с равными полуосями (а = b) называется равносторонней.
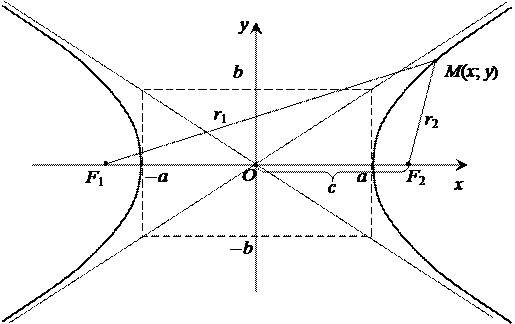 |
Рис. 10