Векторное произведение
Упорядоченная тройка векторов  ,
, 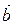 ,
, 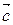 пространства называется правой, если при совмещении их начал в одной точке из конца вектора
пространства называется правой, если при совмещении их начал в одной точке из конца вектора 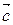 поворот от
поворот от  к
к 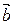 наблюдается против часовой стрелки. В противном случае тройка называется левой. Эта характеристика называется ориентацией тройки векторов.
наблюдается против часовой стрелки. В противном случае тройка называется левой. Эта характеристика называется ориентацией тройки векторов.
Если векторы в тройке сдвинуть по кругу, то ориентация не изменится. Если же поменять местами два вектора, то ориентация изменится на противоположную.
Векторным произведением векторов  и
и 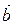 называется вектор
называется вектор 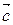 =
=  ´
´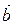 такой, что:
такой, что:
(a)  , где a – угол между векторами;
, где a – угол между векторами;
(b) 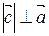 ,
, 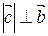 ;
;
(c) векторы  ,
, 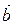 ,
, 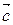 образуют правую тройку.
образуют правую тройку.
Свойства векторного произведения:
1. 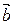 ´
´ = –
= – ´
´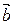 (антикоммутативность).
(антикоммутативность).
2. 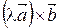 =
= 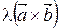 .
.
3. 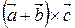 =
=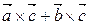 .
.
4. Критерий коллинеарности векторов: 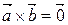 .
.
5. 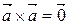 .
.
6. Геометрический смысл векторного произведения: площадь параллелограмма, стороны которого задаются векторами  и
и 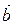 , равна модулю их векторного произведения:
, равна модулю их векторного произведения: 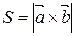 .
.
7. Если  = (a1, a2, a3),
= (a1, a2, a3), 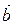 = (b1, b2, b3), причем базисные векторы образуют правую тройку, то
= (b1, b2, b3), причем базисные векторы образуют правую тройку, то 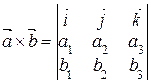 .
.
Пример 1.6.4.Найти векторное произведение векторов  = (2, –1, 3), и
= (2, –1, 3), и
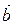 = (3, 2, –2).
= (3, 2, –2).
Решение. По свойству (7) получаем
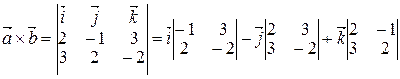 =
=
= 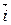 (2 – 6) –
(2 – 6) –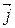 (–4 – 9) +
(–4 – 9) +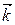 (4 + 3) = –4
(4 + 3) = –4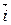 + 13
+ 13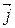 + 7
+ 7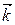 = (–4, 13, 7).
= (–4, 13, 7).
Пример 1.6.5.Найти площадь параллелограмма ABCD, если заданы координаты вершин A(3, 2, 0), C(2, –1, 2) D(1, 3, –4).
Решение. Изобразим параллелограмм ABCD на рисунке, чтобы понять, какие векторы задают стороны параллелограмма. Так как заданы точки A, C, D, то естественно использовать векторы
Так как заданы точки A, C, D, то естественно использовать векторы 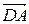 и
и 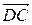 (хотя направление векторов не имеет значения, можно взять противоположные векторы):
(хотя направление векторов не имеет значения, можно взять противоположные векторы):
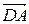 = (3 – 1, 2 – 3, 0 + 4) = (2, –1, 4);
= (3 – 1, 2 – 3, 0 + 4) = (2, –1, 4);
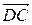 = (2 – 1, –1 – 3, 2 + 4) = (1, –4, 6);
= (2 – 1, –1 – 3, 2 + 4) = (1, –4, 6);
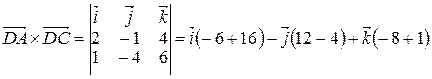 = (10, –8, –7);
= (10, –8, –7);
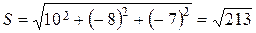 .
.