Определители

Матрица порядка m´n – это матрица с m строками и n столбцами. При m=n имеем квадратную матрицу порядка n.

Определитель квадратной матрицы порядка n – это число, которое ставится в соответствие этой матрице. Определитель матрицы заключен в прямые скобки.

Определители второго и третьего порядка вычисляются по формулам

= ad – bc;

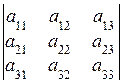= a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ – a₁₃a₂₂a₃₁ – a₁₂a₂₁a₃₃ – a₁₁a₂₃a₃₂. (1)

В последней формуле (1) имеем сумму произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы. Часть этих произведений входит в сумму со знаком «+», остальные – со знаком «–». Чтобы правильно расставить эти знаки, можно применить правило треугольника. Произведение элементов главной диагонали матрицы (выходящей из левого верхнего угла) берется со знаком «+», и с этим же знаком берутся произведения по двум треугольникам, имеющим с этой диагональю параллельную сторону, как на левом рисунке. Произведения по второй, побочной диагонали берутся со знаком «–», как и произведения по двум треугольникам, имеющим с ней параллельную сторону (см. правый рисунок).

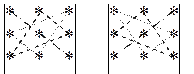
Пример 1.2.1.Вычислим определитель по формуле (1):

=

= 60 + 3 – 24 – 24 – 6 + 30 = 39.

Пример, иллюстрирующий применение определителя, это правило Крамера для решения систем n линейных уравнений с n переменными. Сначала вычисляем определитель D основной матрицы системы. Если D ¹ 0, то система имеет единственное решение. Для нахождения каждого x_i вычисляем определитель D_i матрицы, полученной из основной матрицы заменой i-го столбца на столбец свободных членов. Тогда x_i находим по формуле x_i =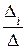для всех i. Этот метод особенно эффективен для решения систем из двух уравнений с двумя переменными; для решения систем с большим числом уравнений и переменных удобнее метод Гаусса.

Пример 1.2.2.Решить систему

Решение. Производим вычисления:

;

; ;

; .

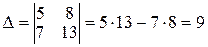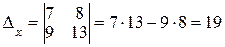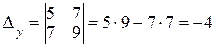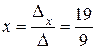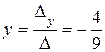Определитель 3-го порядка можно посчитать и по другой формуле, называемой разложением по первой строке:

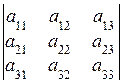= (2)

Структура формулы (2) будет ясна из следующих определений.

Минором элемента a_ij матрицы А (то есть элемента, стоящего и i-ой строке и j-ом столбце) называется определитель M_ij(A) матрицы, полученной из А вычеркиванием i-ой строки и j-го столбца.

Алгебраическим дополнением элемента a_ij матрицы А называется число
A_ij = (–1)^i+j M_ij(A).

Таким образом, формула (2) означает, что определитель получается умножением элементов первой строки на их алгебраические дополнения и суммированием полученных произведений. При применении формулы (2) не стоит выписывать определители второго порядка в правой части, их можно сразу раскрыть, мысленно выделив их в исходной матрице.

Пример 1.2.3.Вычислим определитель из примера 1.2.1 по формуле (2):

=

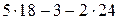= = 39.

Для вычисления определителей более высокого порядка их порядок следует понизить. Для этого пользуются свойствами определителей:

1) если к строке (столбцу) матрицы прибавить другую строку (столбец), умноженную на произвольный скаляр, то ее определитель не изменится;

2) если строку (столбец) матрицы умножить на число l, то на l умножится ее определитель;

3) если поменять местами две строки (столбца) матрицы, то ее определитель поменяет знак;

4) определитель матрицы с нулевой строкой (столбцом) равен 0;

5) определитель матрицы А, у которой все элементы какой-либо строки (столбца), кроме, может быть, a_ij, равны 0, равен (–1)^i+ja_ijM_ij, где M_ij – определитель матрицы, полученной из А вычеркиванием i-ой строки и j-го столбца.

Для понижения порядка определителя выбираем в нем какой-нибудь элемент, обычно равный 1. Остальные элементы столбца, в котором он стоит, надо заменить нулями. Для этого используем строку, в которой стоит выбранный элемент, как опорную. Преобразуем элементы столбца в нули с помощью правила 1), как в методе Гаусса. При этом, возможно, преобразовывать придется строки не только ниже, но и выше выбранной строки. После этого понижаем порядок определителя по правилу 5). Можно, впрочем, поменять строки и столбцы ролями, делая нули не в столбце, а в строке с помощью опорного столбца.

Пример 1.2.4. Вычислить определитель

.

Решение. Мы имеем элемент 1 на пересечении второй строки и второго столбца. Используя вторую строку, сделаем остальные элементы во втором столбце равными 0. Для этого к первой, третьей и четвертой строкам прибавляем вторую, умноженную на –2, –5, –3 соответственно. Получаем:

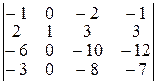= =(–1)²⁺²= =

= 42 + 12 + 0 – 18 – 16 – 0 = 20.

Перед вычислением определителя третьего порядка его упростили, прибавив ко второй строке третью, умноженную на –2.