рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Линейная зависимость. Базис системы векторов
Реферат Курсовая Конспект
Линейная зависимость. Базис системы векторов
Линейная зависимость. Базис системы векторов - раздел Математика, Линейная алгебра и аналитическая геометрия В Геометрии Вектор Понимается Как Направленный Отрезок, Причем Векторы, Получ...
В геометрии вектор понимается как направленный отрезок, причем векторы, полученные один из другого параллельным переносом, считаются равными. Все равные векторы рассматриваются как один и тот же вектор. Начало вектора можно поместить в любую точку пространства или плоскости.
Если в пространстве заданы координаты концов вектора 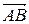 : A(x1, y1, z1), B(x2, y2, z2), то
: A(x1, y1, z1), B(x2, y2, z2), то
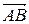 = (x2 – x1, y2 – y1, z2 – z1). (1)
= (x2 – x1, y2 – y1, z2 – z1). (1)
Аналогичная формула имеет место на плоскости. Это значит, что вектор можно записать в виде координатной строки. Операции над векторами, – сложение и умножение на число, над строками выполняются покомпонентно. Это дает возможность расширить понятие вектора, понимая под вектором любую строку чисел. Например, решение системы линейных уравнений, а также любой набор значений переменных системы, можно рассматривать как вектор.
Над строками одинаковой длины операция сложения выполняется по правилу
(a1, a2, … , a n) + (b1, b2, … , bn) = (a1 + b1, a2 + b2, … , a n+ bn). (2)
Умножение строки на число выполняется по правилу
l(a1, a2, … , a n) = (la1, la2, … , la n). (3)
Множество векторов-строк заданной длины n с указанными операциями сложения векторов и умножения на число образует алгебраическую структуру, которая называется n-мерным линейным пространством.
Линейной комбинацией векторов  называется вектор
называется вектор 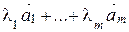 , где λ1, ... , λm – произвольные коэффициенты.
, где λ1, ... , λm – произвольные коэффициенты.
Система векторов 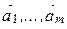 называется линейно зависимой, если существует ее линейная комбинация, равная
называется линейно зависимой, если существует ее линейная комбинация, равная 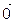 , в которой есть хотя бы один ненулевой коэффициент.
, в которой есть хотя бы один ненулевой коэффициент.
Система векторов  называется линейно независимой, если в любой ее линейной комбинации, равной
называется линейно независимой, если в любой ее линейной комбинации, равной  , все коэффициенты нулевые.
, все коэффициенты нулевые.
Таким образом, решение вопроса о линейной зависимости системы векторов 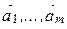 сводится к решению уравнения
сводится к решению уравнения
x1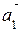 + x2
+ x2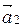 + … + xm
+ … + xm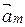 =
= 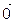 . (4)
. (4)
Если у этого уравнения есть ненулевые решения, то система векторов линейно зависима. Если же нулевое решение является единственным, то система векторов линейно независима.
Для решения системы (4) можно для наглядности векторы записать не в виде строк, а в виде столбцов.

Тогда, выполнив преобразования в левой части, придем к системе линейных уравнений, равносильной уравнению (4). Основная матрица этой системы образована координатами исходных векторов, расположенных по столбцам. Столбец свободных членов здесь не нужен, так как система однородная.
Базисом системы векторов (конечной или бесконечной, в частности, всего линейного пространства) называется ее непустая линейно независимая подсистема, через которую можно выразить любой вектор системы.
Пример 1.5.2.Найти базис системы векторов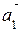 = (1, 2, 2, 4),
= (1, 2, 2, 4), 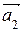 = (2, 3, 5, 1),
= (2, 3, 5, 1), 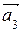 = (3, 4, 8, –2),
= (3, 4, 8, –2), 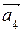 = (2, 5, 0, 3) и выразить остальные векторы через базис.
= (2, 5, 0, 3) и выразить остальные векторы через базис.
Решение. Строим матрицу, в которой координаты данных векторов располагаем по столбцам. Это матрица системы x1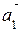 + x2
+ x2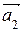 + x3
+ x3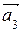 + x4
+ x4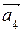 =.
=.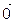 . Приводим матрицу к ступенчатому виду:
. Приводим матрицу к ступенчатому виду:
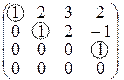
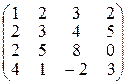 ~
~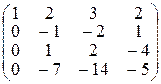 ~
~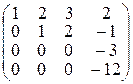 ~
~
Базис данной системы векторов образуют векторы 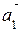 ,
, 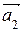 ,
, 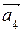 , которым соответствуют ведущие элементы строк, выделенные кружками. Для выражения вектора
, которым соответствуют ведущие элементы строк, выделенные кружками. Для выражения вектора 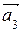 решаем уравнение x1
решаем уравнение x1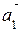 + x2
+ x2 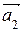 + x4
+ x4 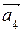 =
= 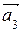 . Оно сводится к системе линейных уравнений, матрица которой получается из исходной перестановкой столбца, соответствующего
. Оно сводится к системе линейных уравнений, матрица которой получается из исходной перестановкой столбца, соответствующего 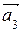 , на место столбца свободных членов. Поэтому при приведении к ступенчатому виду над матрицей будут сделаны те же преобразования, что выше. Значит, можно использовать полученную матрицу в ступенчатом виде, сделав в ней необходимые перестановки столбцов: столбцы с кружками помещаем слева от вертикальной черты, а столбец, соответствующий вектору
, на место столбца свободных членов. Поэтому при приведении к ступенчатому виду над матрицей будут сделаны те же преобразования, что выше. Значит, можно использовать полученную матрицу в ступенчатом виде, сделав в ней необходимые перестановки столбцов: столбцы с кружками помещаем слева от вертикальной черты, а столбец, соответствующий вектору 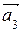 , помещаем справа от черты.
, помещаем справа от черты.

Последовательно находим:
x4 = 0;
x2 = 2;
x1 + 4 = 3, x1 = –1;
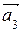 = –
= –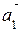 + 2
+ 2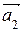 .
.
Замечание. Если требуется выразить через базис несколько векторов, то для каждого из них строится соответствующая система линейных уравнений. Эти системы будут отличаться только столбцами свободных членов. При этом каждая система решается независимо от остальных.
У п р а ж н е н и е 1.4. Найти базис системы векторов и выразить остальные векторы через базис:
а) 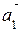 = (1, 3, 2, 0),
= (1, 3, 2, 0), 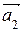 = (3, 4, 2, 1),
= (3, 4, 2, 1), 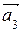 = (1, –2, –2, 1),
= (1, –2, –2, 1), 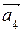 = (3, 5, 1, 2);
= (3, 5, 1, 2);
б) 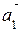 = (2, 1, 2, 3),
= (2, 1, 2, 3), 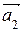 = (1, 2, 2, 3),
= (1, 2, 2, 3), 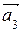 = (3, –1, 2, 2),
= (3, –1, 2, 2), 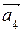 = (4, –2, 2, 2);
= (4, –2, 2, 2);
в) 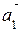 = (1, 2, 3),
= (1, 2, 3), 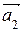 = (2, 4, 3),
= (2, 4, 3), 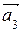 = (3, 6, 6),
= (3, 6, 6), 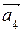 = (4, –2, 1);
= (4, –2, 1); 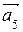 = (2, –6, –2).
= (2, –6, –2).
В заданной системе векторов базис обычно можно выделить разными способами, но во всех базисах будет одинаковое число векторов. Число векторов в базисе линейного пространства называется размерностью пространства. Для n-мерного линейного пространства n – это размерность пространства, так как это пространство имеет стандартный базис 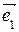 = (1, 0, … , 0),
= (1, 0, … , 0), 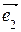 = (0, 1, … , 0), … ,
= (0, 1, … , 0), … ,  = (0, 0, … , 1). Через этот базис любой вектор
= (0, 0, … , 1). Через этот базис любой вектор  = (a1, a2, … , an) выражается следующим образом:
= (a1, a2, … , an) выражается следующим образом:
 = (a1, 0, … , 0) + (0, a2, … , 0) + … + (0, 0, … , an) =
= (a1, 0, … , 0) + (0, a2, … , 0) + … + (0, 0, … , an) =
= a1(1, 0, … , 0) + a2(0, 1, … , 0) + … + an(0, 0, … ,1) = a1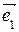 + a2
+ a2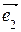 +… + an
+… + an .
.
Таким образом, компоненты в строке вектора  = (a1, a2, … , an) – это его коэффициенты в разложении через стандартный базис.
= (a1, a2, … , an) – это его коэффициенты в разложении через стандартный базис.
– Конец работы –
Эта тема принадлежит разделу:
Линейная алгебра и аналитическая геометрия
Алгебра матриц... На множестве матриц определены операции сложения умножения на число... Складывать можно прямоугольные матрицы одного и того же порядка Сложение выполняется поэлементно...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Линейная зависимость. Базис системы векторов
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов