Задача 3.
Указания к задаче.
Meтод Жордана
Система линейных алгебраических уравнений называется системой с базисом, если в каждом ее уравнении имеется выделенное неизвестное, не входящее ни в одно из остальных уравнений и входящее в данное уравнение с коэффициентом, равным единице При соответствующей нумерации неизвестных (в k-м уравнении выделенной служит неизвестная xk) система с базисом имеет вид:
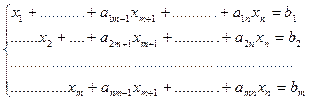 |
(A)
Выделенные неизвестные x1, x2……., xm называют базисными, а остальные – свободными (небазисными).
Если члены, содержащие свободные неизвестные, перенести в правую часть, то система с базисом запишется в следующем эквивалентном виде:
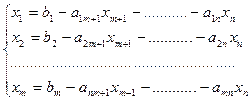 |
(B)
Решение системы (В) получается сразу: надо придать свободным неизвестным любые значения и определить из системы (В) отвечающие им значения базисных неизвестных. Ясно, что полученный таким образом набор значений x1, x2……., xm, xm+1 ,…. xn ,будет решением системы (В) и, тем самым, решением исходной системы (А). Также ясно, что таким образом может быть получено любое решение исходной системы. Другими словами: соотношения (В) дают общий вид решения системы (А).
 Пример
Пример
В системе базисными неизвестными служат x2, x5, x6. Решая систему относительно этих неизвестных, получим:

Эти формулы дают общее решение исходной системы: при любых конкретных значениях свободных неизвестных x1, x3, x4, они дают решение системы, и любое решение может быть получено таким путем. Положив, например, x1 = x3 = x4=0, получим для базисных неизвестных x2=10, x5=8, x6=15 и решение системы - вектор X(0) = (0;10;0;0,8;15). При x1=1, x3=-1, x4=4 получим значения x2=10-3+2+2=11 , x5=8-2-5-4=--3. x6= 15-4+3+10=24 и решение - вектор. X(1) = (1;11;-1;4;-3;24).
Заметим, что решение, в котором все свободные неизвестные равны нулю, называется базисным. В нашем примере - это X(0).
Решение общей системы линейных алгебраических уравнений методом Жордана заключается в планомерном преобразовании системы к эквивалентной ей системе с базисом.
 Алгоритм метода опишем на конкретном примере системы:
Алгоритм метода опишем на конкретном примере системы:
(1)
(2)
(3)
(4)
Систему рассматриваем для двух возможных значений правой части b3, третьего уравнения b3=15 и b3=10.
Отдельный шаг преобразования заключается в назначении в одном из уравнений неизвестной, которая должна быть в нем базисной, и исключении ее из остальных уравнений. Этот шаг повторяется до тех пор пока это возможно (см. ниже).
Выделим в первом уравнении неизвестную х2. Так как коэффициент при базисной неизвестной должен равняться единице, то делим обе части уравнения на коэффициент при х1 (т.е. на -1). Получим. -7х1+x2-5x3+х4-2x5=-12. (1’)
Пользуясь уравнением (1’), исключим неизвестную х2 из остальных уравнений. Для этого умножаем (1’) на - 4 и складываем с уравнением (2). Затем умножаем (1’) на 6 и складываем с уравнением (3) Затем умножаем (1') на - 2 и складываем с уравнением (4).
 (2’)
(2’)
(3’)
(4’)
Базисная переменная в первом уравнении выделена. При этом получена эквивалентная система (1’) - (4’).
Аналогичным образом выбираем неизвестную х4, а уравнении (2’) и превращаем ее в базисную и т.д. Весь алгоритм оформляется в виде последовательных преобразований (описанного выше типа) таблицы, в которой записана вся информация о системе, каждая строка таблицы дает запись одного уравнения. В первом столбце записаны правые части уравнений, в остальных - коэффициенты при неизвестных см. на с. 19 Т.1.
Каждый шаг (так называемая большая итерация) требует выполнения следующих действий:
1. Выбор главного(ключевого или ведущего) элемента
За главный элемент можно принять любой отличный от нуля коэффициент при одном из неизвестных. В каждой строке главный элемент может выбираться только один раз. Невозможность выбора главного элемента говорит об окончании вычислений. Выбранный элемент заключается в квадратик. Его строку и столбец будем называть ключевыми.