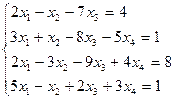Преобразование не ключевых строк
Для преобразования не ключевой строки нужно каждый элемент преобразованной ключевой строки умножить на дополнительный множитель преобразуемой строки и добавить к соответствующему элементу.
5. Если в ходе вычислений появляется строка вида:
| b | x1 | x2 | xn | |
| b≠0 |
т.е. строка, в которой все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, то система не имеет решений.
Действительно, всякое решение системы должно удовлетворять уравнению, записанному в этой строке, которое имеет вид:
 ...................................................
...................................................
Поскольку его левая часть равна нулю для любых значений x1, x2,…, xn, а правая часть отлична от нуля, то ему не может удовлетворять ни один такой набор.
6. Если в ходе вычислений появляется строка, состоящая из одних нулей, то ее можно удалить из таблицы, так как такая строка отвечает уравнению:
 |
которому удовлетворяет любой набор значений x1, x2,…, xn и поэтому ее можно не учитывать.
Заметим, что появление строки из одних нулей свидетельствует о том, что записанное в ней уравнение является следствием других уравнений системы.
Если при применении алгоритма не возникает противоречивой ситуации, описанной в п.5, то в каждой строке заключительной таблицы (т.е. в каждом уравнении) имеется базисная неизвестная, и система оказывается приведенной к эквивалентной системе с базисом.
Применим описанный алгоритм к системе из примера.
| b | x1 | x2 | x3 | x4 | x5 | Подмножитель |
| 15(10) | -1 | -1 -6 | -1 -1 | -8 | -3 -1 | - -4 -2 |
| -12 57(-62) | -7 -31 | -5 -19 | -2 | -2 -5 | -1 - -3 | |
| -40,5 28,5 0(-5) -57,5 | -22,5 15,5 -33,5 | -14,5 9,5 -19,5 | -4,5 2,5 -4,5 | 4,5 -2,5 - - | ||
| -31/9 115/9 | -28/9 67/9 | -4/3 19/3 |
Т.1
*
Т.2
*
*
Т.3
*
Т.4*
*
В Т.1 за главный элемент выбран коэффициент при x2 в 1-м уравнении. В Т.2 соответствующая строка помечена звездочкой в знак того, что в ней выбирался главный элемент. Затем эта строка умножается на соответствующие множители и добавляется к строкам исходной таблицы.
Дальнейшие действия аналогичны и понятны из приведенных таблиц.
В Т.З появляется строка, в которой все коэффициенты при неизвестных равны нулю.
Если в исходной таблице свободный член b3=10, то появилась противоречивая строка,
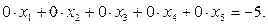 |
Следовательно, система не имеет решений.
Если же b3 = 15, то третья строка таблицы Т.З состоит из одних нулей и удаляется из таблицы.
Дальнейшее решение (Т.4) касается только этого случая.
В Т.4 все строки помечены звездочками, т.е. главный элемент появлялся, в каждой из них, и выбор его, более невозможен.
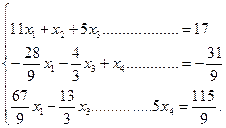
Работа алгоритма закончена. Т.4 дает запись системы с базисом, эквивалентной исходной:
Общее решение последней, а значит, и исходной системы даете формулами:

Например, при x1=1 и x3=1 получаем x,=1, x4=1, x5=1 т.е. получаем решение X=(1;1;1;1;1). Положив x1=x3=0 получаем базисное решение Xбаз.=(0;17;0;-31/9;ll5/9), В заключение этого пункта отметим, что метод Жордана позволяет полностью исследовать любую систему линейных алгебраических уравнений.
а) если в ходе вычислений появляется «противоречивая строка»
| b≠0 |
то система не имеет решений. Уравнение, отвечающее этой строке, противоречит уравнениям, строки которых помечены звездочками (т.е. в которых выделялся главный элемент);
б) если «противоречивая строка» в ходе вычислении не появлялась, то система имеет решение. Его общий вид получается из последней таблицы. Если есть свободные неизвестные, то система имеет бесконечно много решений. Если свободных переменных нет, то система имеет единственное решение;
в) появление нулевой строки показывает, что соответствующее ей уравнение является следствием уравнений, помеченных звездочками в данной таблице. Число независимых уравнений равно числу ненулевых строк последней таблицы (в случае разрешимости системы).
3.1-3.20. Решить систему методом Жордано - Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.
3.1. 
3.2. 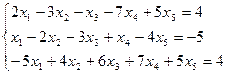
3.3. 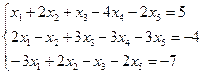
3.4. 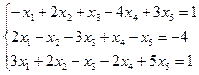
3.5. 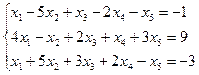
3.6. 
3.7. 
3.8. 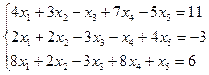
3.9. 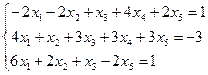
3.10. 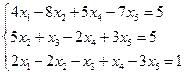
3.11. 
3.12. 
3.13. 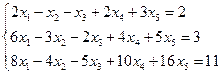
3.14. 
3.15. 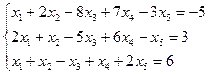
3.16. 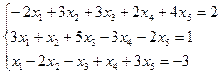
3.17. 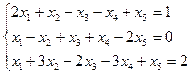
3.18. 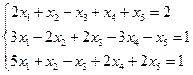
3.19. 
3.20.