рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Задача 4.
Реферат Курсовая Конспект
Задача 4.
Задача 4. - раздел Математика, ЛИНЕЙНАЯ АЛГЕБРА Указания К Задаче. Задача 4. Связана С Действиями Над Матрицами. Для...
Указания к задаче.
Задача 4. связана с действиями над матрицами. Для решения этой задачи следует использовать следующие сведения:
1. Всякая система m·n, расположенных в виде прямоугольной таблицы, содержащей
m строк и n столбцов, называется матрицей размера m×n и записывается в виде:

2). Матрица размера m×m (количество строчек равно количеству столбцов) называется квадратной матрицей порядка m.
3). Диагональ квадратной матрицы, идущая от левого верхнего утла к правому нижнему, называется главной диагональю, а вторая диагональ называется побочной.
4). Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные цифры нули, называется единичной матрицей n, обозначается следующим образом:
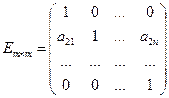
5) Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах, т.е. если

6). Произведением матрицы 
на число α называется матрица Cm×n, каждый элемент которой равен произведению соответствующего элемента матрицы Am×n на число α.
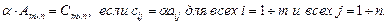
7). Суммой двух матриц одной размерности
 называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц Am×n и Bm×n , т.е.
называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц Am×n и Bm×n , т.е. 
8). Умножение матрицы на матрицу
Пусть даны две матрицы Am×n и Bn×k, таких что число столбцов матрица А равно числу строк матрицы В. Тогда произведением матриц называется матрица Cm×k, каждый элемент которой cij равен сумме попарных произведений элементов i–й строки матрицы А на соответствующие элементы j-го столбца матрица В, т.е.
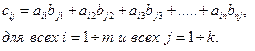
Заметим, что A·B≠B·A
9). Определители квадратных матриц
Каждой квадратной матрице ставится в соответствие число, обозначаемое
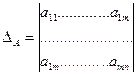 |
Рассмотрим определителя для матриц первого, второго и третьего порядков:
а). Пусть А=(а11), тогда ΔА=│a11│=a11. (1)
Из формулы (1) следует, что определитель для матрицы первого порядка совпадает с элементами матрицы А1·1.
б) Пусть  (2)
(2)
Из формулы (2) следует, что определитель матрицы второго порядка равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.
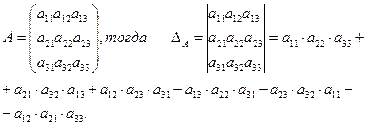
в). Пусть (3)
Формулу (3) запомнить значительно труднее, чем (1) и (2), но это и не требуется, так как существуют различные правила, позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.
Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2.

Первые три слагаемые, входящие в формулу (3) со своим знаком, подсчитываются в соответствии со схемой 1, а следующие три слагаемые, входящие с противоположным знаком, подсчитываются по схеме 2.
10). Алгебраическим дополнением элемента аij квадратной матрицы Am×n называется число Аij, вычисляемое по формуле:
Aij=(-1)i+j·Mij, где Mij- определитель, полученный из определителя матрицы Am×n удалением строки с номером i и столбца с номером j .
11). Обратная матрица
Матрица А-1 называется обратной к матрице А, если A·A-1=A-1·A=E , где Е - единичная матрица. Из определения следует, что матрицы А и А-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от

12). Решение простейших алгебраических уравнений
а) А·X=В, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X=А-1·В.
б) X·А=В, - где ,А и В заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X= А-1·X.
Примеры1). Выполнить действия: (А+2В)·С, где
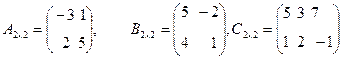
Решение

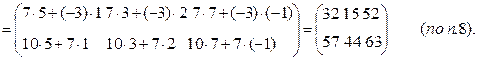
2). Найти А-1, если 
Решение

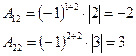
 , Тогда
, Тогда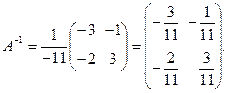
Проверим, верно ли нашли А-1. Для этого умножим А на А-1 и убедимся, что получим единичную матрицу.

3). Решить уравнение AX-B=C, где 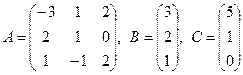
Решение
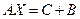


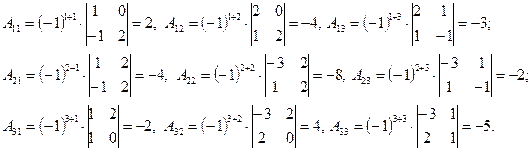
Тогда 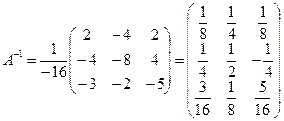 ,
,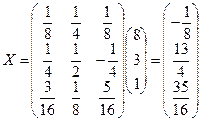
Проверка
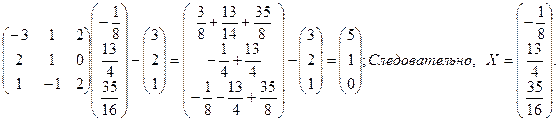
Задача 4. Решить матричное уравнение, сделать проверку.
4.1. 
4.2. 
4.3. 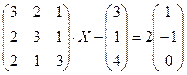
4.4. 
4.5. 
4.6. 
4.7. 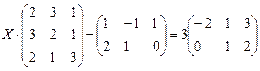
4.8. 
4.9. 
4.10. 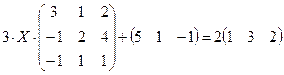
4.11. 
4.12. 
4.13. 
4.14. 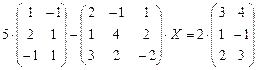
4.15. 
4.16. 
4.17. 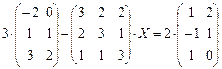
4.18. 
4.19. 
4.20. 
Задача 5
5.1-5.20. Найти собственные числа и собственные векторы матрицы.
5.1.  5.2.
5.2.  5.3.
5.3. 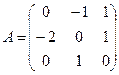 5.4.
5.4. 
5.5.  5.6.
5.6.  5.7.
5.7.  5.8.
5.8. 
5.9. 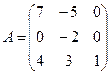 5.10.
5.10. 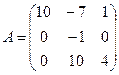 5.11.
5.11.  5.12.
5.12. 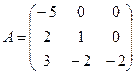
5.13.  5.14.
5.14. 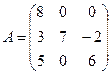 5.15.
5.15.  5.16 .
5.16 . 
5.17. 5.18.
5.18.  5.19.
5.19.  5.20.
5.20. 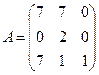
Указания к задаче.
Число λ называется собственным числом матрицы А n-го порядка, если существует такой ненулевой n-мерный вектор Х, что АХ= λХ. Этот ненулевой вектор Х называется собственным вектором матрицы А, соответствующим её собственному числу λ.
Множество всех собственных чисел матрицы А совпадает с множеством всех решений уравнения 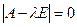 , которое называется характеристическим уравнением матрицы А.
, которое называется характеристическим уравнением матрицы А.
Множество всех собственных векторов матрицы А, соответствующих её собственному числу λ, совпадает с множеством всех ненулевых решений системы однородных уравнений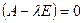
Задача. Найти собственные числа и собственные векторы матрицы 
Решение. Найдём характеристическое уравнение матрицы А:


При вычислении данного определителя использовалось его разложение по элементам 3 столбца.
Найдём теперь собственные числа матрицы А – корни характеристического уравнения
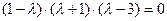 . Получаем λ1 = 3, λ2 = 1, λ3 = -1.
. Получаем λ1 = 3, λ2 = 1, λ3 = -1.
Далее собственные векторы матрицы А, соответствующие каждому из собственных чисел.
Пусть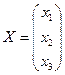 искомый собственный вектор. Тогда система однородных уравнении
искомый собственный вектор. Тогда система однородных уравнении 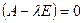 будет иметь вид:
будет иметь вид:  или
или  (1)
(1)
Эта однородная система линейных уравнений имеет множество решений, так как её определитель равен нулю.
При λ = λ1= 3 система (1) принимает вид:  . Общее решение этой системы
. Общее решение этой системы  , где х2 – любое число.
, где х2 – любое число.
В качестве собственного вектора достаточно взять любое частное решение. Пусть, например, х2 = 1, тогда собственный вектор, , соответствующий собственному числу λ1=3, имеет вид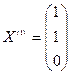
При λ = λ1 = 1 система (1) принимает вид:  . Общее решение этой системы
. Общее решение этой системы , где х3 – любое число.
, где х3 – любое число.
Пусть, например, х3 = 1, тогда собственный вектор, , соответствующий собственному числу λ2=1,
имеет вид .
.
Аналогично при λ = λ3 = -1 система (1) принимает вид:  . Общее решение этой системы
. Общее решение этой системы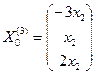 , где х2 – любое число.
, где х2 – любое число.
Пусть, например, х2 = 1, тогда собственный вектор, , соответствующий собственному числу λ2=-1, имеет вид . Ответ: λ1=3,λ2=1,λ3= -1,
. Ответ: λ1=3,λ2=1,λ3= -1, 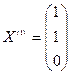 ,
, ,
,
– Конец работы –
Эта тема принадлежит разделу:
ЛИНЕЙНАЯ АЛГЕБРА
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Санкт Петербургский государственный... Филиал федерального государственного бюджетного образовательного учреждения...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задача 4.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов