Задача 4.
Указания к задаче.
Задача 4. связана с действиями над матрицами. Для решения этой задачи следует использовать следующие сведения:
1. Всякая система m·n, расположенных в виде прямоугольной таблицы, содержащей
m строк и n столбцов, называется матрицей размера m×n и записывается в виде:

2). Матрица размера m×m (количество строчек равно количеству столбцов) называется квадратной матрицей порядка m.
3). Диагональ квадратной матрицы, идущая от левого верхнего утла к правому нижнему, называется главной диагональю, а вторая диагональ называется побочной.
4). Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные цифры нули, называется единичной матрицей n, обозначается следующим образом:
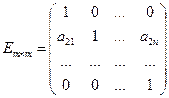
5) Две матрицы одной размерности равны друг другу, если равны все элементы этих матриц, стоящие на одинаковых местах, т.е. если

6). Произведением матрицы 
на число α называется матрица Cm×n, каждый элемент которой равен произведению соответствующего элемента матрицы Am×n на число α.
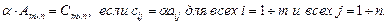
7). Суммой двух матриц одной размерности
 называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц Am×n и Bm×n , т.е.
называется матрица Cm×n той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц Am×n и Bm×n , т.е. 
8). Умножение матрицы на матрицу
Пусть даны две матрицы Am×n и Bn×k, таких что число столбцов матрица А равно числу строк матрицы В. Тогда произведением матриц называется матрица Cm×k, каждый элемент которой cij равен сумме попарных произведений элементов i–й строки матрицы А на соответствующие элементы j-го столбца матрица В, т.е.
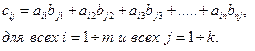
Заметим, что A·B≠B·A
9). Определители квадратных матриц
Каждой квадратной матрице ставится в соответствие число, обозначаемое
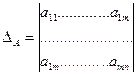 |
Рассмотрим определителя для матриц первого, второго и третьего порядков:
а). Пусть А=(а11), тогда ΔА=│a11│=a11. (1)
Из формулы (1) следует, что определитель для матрицы первого порядка совпадает с элементами матрицы А1·1.
б) Пусть  (2)
(2)
Из формулы (2) следует, что определитель матрицы второго порядка равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.
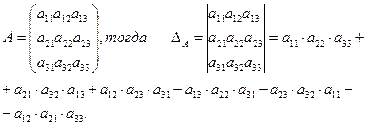
в). Пусть (3)
Формулу (3) запомнить значительно труднее, чем (1) и (2), но это и не требуется, так как существуют различные правила, позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.
Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2.

Первые три слагаемые, входящие в формулу (3) со своим знаком, подсчитываются в соответствии со схемой 1, а следующие три слагаемые, входящие с противоположным знаком, подсчитываются по схеме 2.
10). Алгебраическим дополнением элемента аij квадратной матрицы Am×n называется число Аij, вычисляемое по формуле:
Aij=(-1)i+j·Mij, где Mij- определитель, полученный из определителя матрицы Am×n удалением строки с номером i и столбца с номером j .
11). Обратная матрица
Матрица А-1 называется обратной к матрице А, если A·A-1=A-1·A=E , где Е - единичная матрица. Из определения следует, что матрицы А и А-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от

12). Решение простейших алгебраических уравнений
а) А·X=В, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X=А-1·В.
б) X·А=В, - где ,А и В заданные матрицы, причем А - квадратная матрица, определитель которой ≠0. Тогда X= А-1·X.
Примеры1). Выполнить действия: (А+2В)·С, где
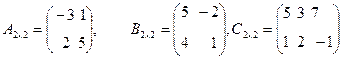
Решение

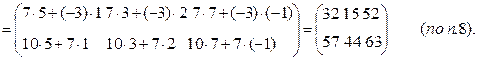
2). Найти А-1, если 
Решение

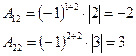
 , Тогда
, Тогда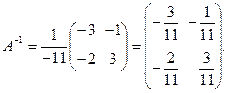
Проверим, верно ли нашли А-1. Для этого умножим А на А-1 и убедимся, что получим единичную матрицу.

3). Решить уравнение AX-B=C, где 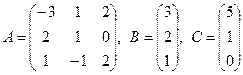
Решение
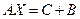


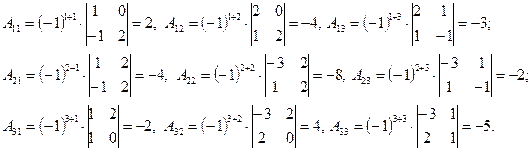
Тогда 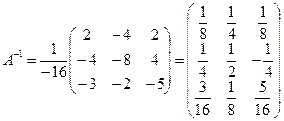 ,
,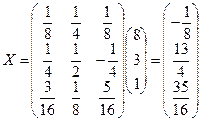
Проверка
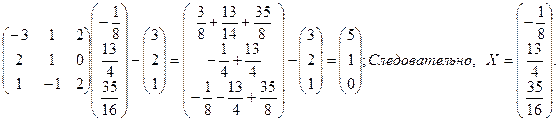
Задача 4. Решить матричное уравнение, сделать проверку.
4.1. 
4.2. 
4.3. 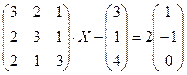
4.4. 
4.5. 
4.6. 
4.7. 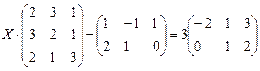
4.8. 
4.9. 
4.10. 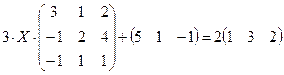
4.11. 
4.12. 
4.13. 
4.14. 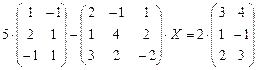
4.15. 
4.16. 
4.17. 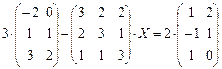
4.18. 
4.19. 
4.20. 
Задача 5
5.1-5.20. Найти собственные числа и собственные векторы матрицы.
5.1.  5.2.
5.2.  5.3.
5.3. 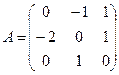 5.4.
5.4. 
5.5.  5.6.
5.6.  5.7.
5.7.  5.8.
5.8. 
5.9. 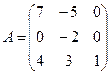 5.10.
5.10. 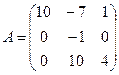 5.11.
5.11.  5.12.
5.12. 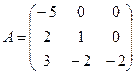
5.13.  5.14.
5.14. 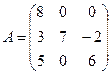 5.15.
5.15.  5.16 .
5.16 . 
5.17. 5.18.
5.18.  5.19.
5.19.  5.20.
5.20. 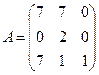
Указания к задаче.
Число λ называется собственным числом матрицы А n-го порядка, если существует такой ненулевой n-мерный вектор Х, что АХ= λХ. Этот ненулевой вектор Х называется собственным вектором матрицы А, соответствующим её собственному числу λ.
Множество всех собственных чисел матрицы А совпадает с множеством всех решений уравнения 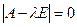 , которое называется характеристическим уравнением матрицы А.
, которое называется характеристическим уравнением матрицы А.
Множество всех собственных векторов матрицы А, соответствующих её собственному числу λ, совпадает с множеством всех ненулевых решений системы однородных уравнений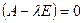
Задача. Найти собственные числа и собственные векторы матрицы 
Решение. Найдём характеристическое уравнение матрицы А:


При вычислении данного определителя использовалось его разложение по элементам 3 столбца.
Найдём теперь собственные числа матрицы А – корни характеристического уравнения
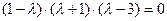 . Получаем λ1 = 3, λ2 = 1, λ3 = -1.
. Получаем λ1 = 3, λ2 = 1, λ3 = -1.
Далее собственные векторы матрицы А, соответствующие каждому из собственных чисел.
Пусть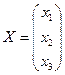 искомый собственный вектор. Тогда система однородных уравнении
искомый собственный вектор. Тогда система однородных уравнении 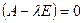 будет иметь вид:
будет иметь вид:  или
или  (1)
(1)
Эта однородная система линейных уравнений имеет множество решений, так как её определитель равен нулю.
При λ = λ1= 3 система (1) принимает вид:  . Общее решение этой системы
. Общее решение этой системы  , где х2 – любое число.
, где х2 – любое число.
В качестве собственного вектора достаточно взять любое частное решение. Пусть, например, х2 = 1, тогда собственный вектор, , соответствующий собственному числу λ1=3, имеет вид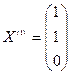
При λ = λ1 = 1 система (1) принимает вид:  . Общее решение этой системы
. Общее решение этой системы , где х3 – любое число.
, где х3 – любое число.
Пусть, например, х3 = 1, тогда собственный вектор, , соответствующий собственному числу λ2=1,
имеет вид .
.
Аналогично при λ = λ3 = -1 система (1) принимает вид:  . Общее решение этой системы
. Общее решение этой системы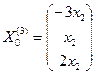 , где х2 – любое число.
, где х2 – любое число.
Пусть, например, х2 = 1, тогда собственный вектор, , соответствующий собственному числу λ2=-1, имеет вид . Ответ: λ1=3,λ2=1,λ3= -1,
. Ответ: λ1=3,λ2=1,λ3= -1, 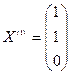 ,
, ,
,