III. ОБРАЗЕЦ ВЫПОЛНЕНИЯ ТИПОВОГО РАСЧЕТА

 

1. Вычислить определитель четвертого порядка с помощью свойств определителей:

.

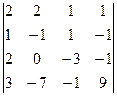Решение

Для удобства преобразований поменяем местами 1-ю и 2-ю строки, после чего поставим перед определителем знак минус (т. к. при перестановке строк местами определитель меняет знак):

.

Преобразуем данный определитель так, чтобы в первом столбце все элементы, кроме одного, обратились в ноль; 1-ю строку умножим на (-2) и сложим со 2-й и 3-й строками, затем 1-ю строку умножим на (-3) и сложим с 4-й:

.

Раскладывая определитель по элементам первого столбца, получим:

.

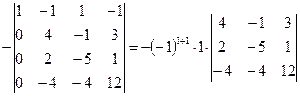Из 3-й строки вынесем общий множитель за знак определителя и поменяем местами 1-ю и 3-ю строки:

.

1-ю строку умножим на 2, сложим со 2-й; затем 1-ю строку умножим на 4, сложим с 3-й:

.

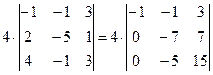Разложим определитель по первому столбцу:

.

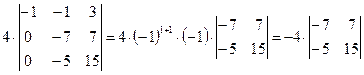Из обеих строк определителя вынесем общие множители и вычислим его:

.

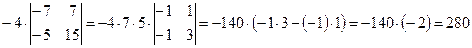Итак, .

 

2. Найти обратную матрицу и сделать проверку:

.

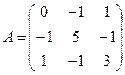Решение

Вычислим определитель данной матрицы (разложим по первой строке):

,

следовательно, обратная матрица 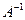существует.

Выпишем алгебраические дополнения матрицы A:

,	,	,
,	,	,
,	,	.

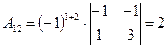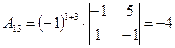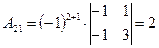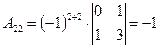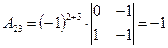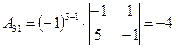Составим матрицу 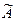, состоящую из алгебраических дополнений матрицы A:

.

Матрица, обратная к матрице A, будет иметь вид:

.

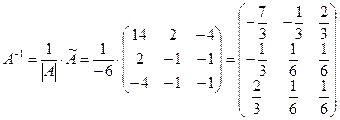Проверка

.

 

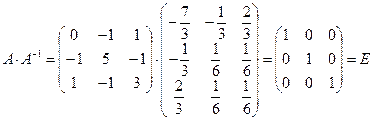3. Решить матричное уравнение:

.

Решение

Матричное уравнение задано в виде . Следовательно,

,

,

.

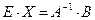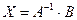Найдем матрицу, обратную к матрице A.

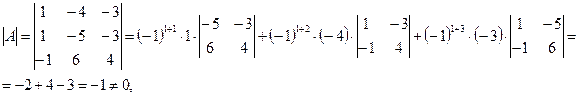
следовательно, обратная матрица 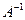существует.

Выпишем алгебраические дополнения матрицы A:

,	,	,
,	,	,
,	,	.

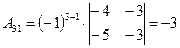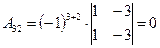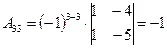Составим матрицу 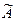, состоящую из алгебраических дополнений матрицы A:

.

Матрица, обратная к матрице A, будет иметь вид:

.

.

 

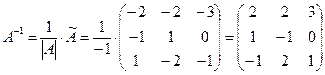Искомая матрица имеет вид:

.

 

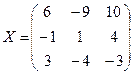4. Решить систему линейных уравнений методом Крамера:

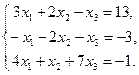
Решение

Вычислим определитель системы:

.

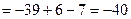Вычислим определители , в которых вместо первого, второго и третьего столбцов соответственно стоит столбец из свободных членов:

,

,

.

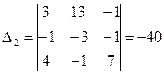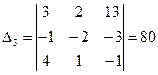Найдем значения неизвестных :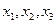

,

,

.

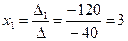Итак, , , .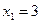

 

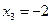5. Решить систему линейных уравнений матричным методом:

Решение

Перепишем систему уравнений в виде матричного уравнения:

, где , , .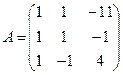

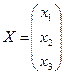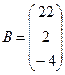Имеем:

,

,

.

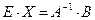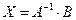Найдем матрицу, обратную к матрице A:

,

следовательно, обратная матрица 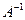существует.

Выпишем алгебраические дополнения матрицы A:

,	,	,
,	,	,
,	,	.

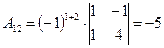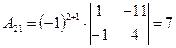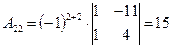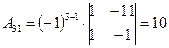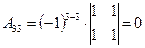Составим матрицу 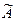, состоящую из алгебраических дополнений матрицы A:

.

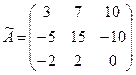Матрица, обратная к матрице A, будет иметь вид:

.

.

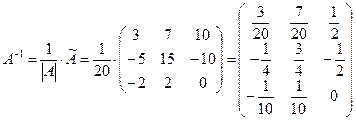Итак, , , .

 

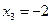6. Решить систему линейных уравнений методом Гаусса:

Решение

Вычислим определитель системы:

.

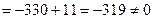Следовательно, система совместна и имеет единственное решение.

Составим расширенную матрицу системы и приведем ее к треугольному виду.

~ + +

~~ + ~.

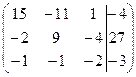Из полученной матрицы составим систему линейных уравнений и найдем неизвестные с помощью обратного хода Гаусса:

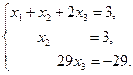Отсюда: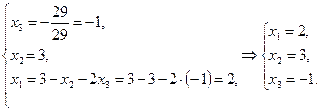

Ответ: , , .

 

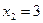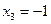7. Решить систему линейных уравнений методом Жордановых исключений:

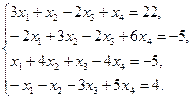
Решение

Составим таблицу коэффициентов системы и преобразуем ее так, чтобы на ее главной диагонали стояли только единицы, а все остальные элементы были равны нулю.

 

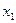
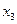
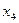
		–2
–2		–2		–5
			–4	–5
–1	–1	–3
	1/3	–2/3	1/3	22/3
	11/3	–10/3	20/3	29/3
	11/3	5/3	–13/3	–37/3
	–2/3	–11/3	16/3	34/3
		–4/11	–3/11	71/11
		–10/11	20/11	29/11
			–11	–22
		–47/11	72/11	144/11
			–59/55	267/55
			–2/11	–15/11
			–11/5	–22/5
			–157/55	–314/55

Из таблицы имеем:

 

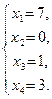
8. Найти общее решение и фундаментальную систему решений системы однородных линейных уравнений:

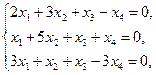
Решение

Запишем матрицу системы и преобразуем ее к ступенчатому виду:

~~~.

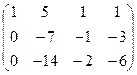Ранг матрицы равен 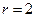, значит фундаментальная система решений состоит из решений. Перепишем преобразованную систему:

 

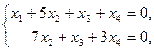
где 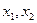– базисные неизвестные, 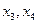– свободные неизвестные.

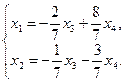
Введем обозначения 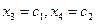и запишем общее решение системы:

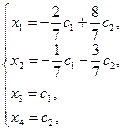
где 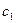и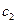– произвольные постоянные.

Придадим произвольным постоянным 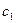и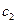последовательно значения и соответственно, получим:

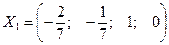и 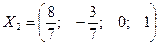– фундаментальная система решений.

 

9. Найти матрицу линейного оператора A в базисе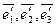, если в стандартном базисематрица линейного оператора А имеет вид:

.

Решение

Матрицы 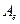и линейного оператора A связаны соотношением , где C – матрица перехода от базиса 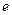к базису 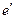, она имеет вид:

, .

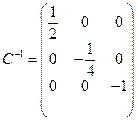Подставим матрицы 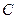, , 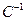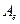в соотношение

.

Итак, .