III. ОБРАЗЕЦ ВЫПОЛНЕНИЯ ТИПОВОГО РАСЧЕТА
1. Вычислить определитель четвертого порядка с помощью свойств определителей:
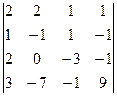 .
.
Решение
Для удобства преобразований поменяем местами 1-ю и 2-ю строки, после чего поставим перед определителем знак минус (т. к. при перестановке строк местами определитель меняет знак):
 .
.
Преобразуем данный определитель так, чтобы в первом столбце все элементы, кроме одного, обратились в ноль; 1-ю строку умножим на (-2) и сложим со 2-й и 3-й строками, затем 1-ю строку умножим на (-3) и сложим с 4-й:
 .
.
Раскладывая определитель по элементам первого столбца, получим:
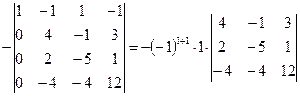 .
.
Из 3-й строки вынесем общий множитель за знак определителя и поменяем местами 1-ю и 3-ю строки:
 .
.
1-ю строку умножим на 2, сложим со 2-й; затем 1-ю строку умножим на 4, сложим с 3-й:
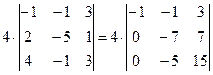 .
.
Разложим определитель по первому столбцу:
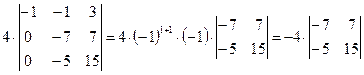 .
.
Из обеих строк определителя вынесем общие множители и вычислим его:
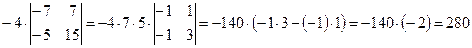 .
.
Итак,  .
.
2. Найти обратную матрицу и сделать проверку:
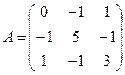 .
.
Решение
Вычислим определитель данной матрицы (разложим по первой строке):
 ,
,
следовательно, обратная матрица 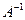 существует.
существует.
Выпишем алгебраические дополнения матрицы A:
 , ,
| 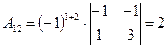 , ,
| 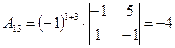 , ,
|
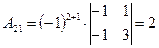 , ,
| 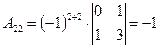 , ,
| 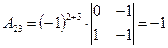 , ,
|
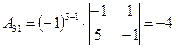 , ,
|  , ,
|  . .
|
Составим матрицу 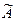 , состоящую из алгебраических дополнений матрицы A:
, состоящую из алгебраических дополнений матрицы A:
 .
.
Матрица, обратная к матрице A, будет иметь вид:
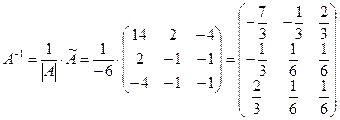 .
.
Проверка
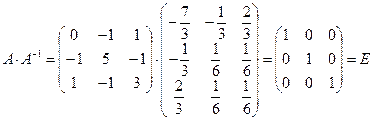 .
.
3. Решить матричное уравнение:
 .
.
Решение
Матричное уравнение задано в виде  . Следовательно,
. Следовательно,
 ,
,
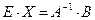 ,
,
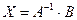 .
.
Найдем матрицу, обратную к матрице A.
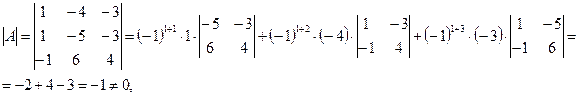
следовательно, обратная матрица 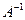 существует.
существует.
Выпишем алгебраические дополнения матрицы A:
 , ,
|  , ,
|  , ,
|
 , ,
|  , ,
|  , ,
|
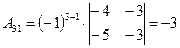 , ,
| 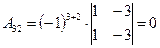 , ,
| 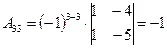 . .
|
Составим матрицу 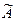 , состоящую из алгебраических дополнений матрицы A:
, состоящую из алгебраических дополнений матрицы A:
 .
.
Матрица, обратная к матрице A, будет иметь вид:
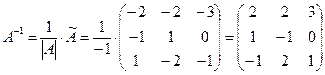 .
.

 .
.
Искомая матрица имеет вид:
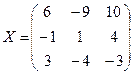 .
.
4. Решить систему линейных уравнений методом Крамера:
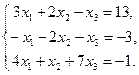
Решение
Вычислим определитель системы:

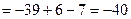 .
.
Вычислим определители  , в которых вместо первого, второго и третьего столбцов соответственно стоит столбец из свободных членов:
, в которых вместо первого, второго и третьего столбцов соответственно стоит столбец из свободных членов:
 , ,
| 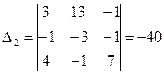 , ,
| 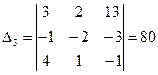 . .
|
Найдем значения неизвестных 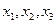 :
:
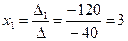 , ,
|  , ,
|  . .
|
Итак, 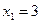 ,
,  ,
, 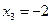 .
.
5. Решить систему линейных уравнений матричным методом:

Решение
Перепишем систему уравнений в виде матричного уравнения:
 , где
, где 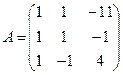 ,
, 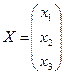 ,
, 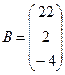 .
.
Имеем:
 ,
,
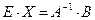 ,
,
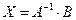 .
.
Найдем матрицу, обратную к матрице A:

 ,
,
следовательно, обратная матрица 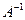 существует.
существует.
Выпишем алгебраические дополнения матрицы A:
 , ,
| 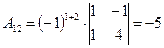 , ,
|  , ,
|
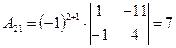 , ,
| 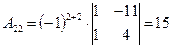 , ,
|  , ,
|
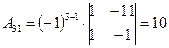 , ,
|  , ,
| 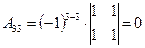 . .
|
Составим матрицу 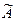 , состоящую из алгебраических дополнений матрицы A:
, состоящую из алгебраических дополнений матрицы A:
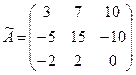 .
.
Матрица, обратная к матрице A, будет иметь вид:
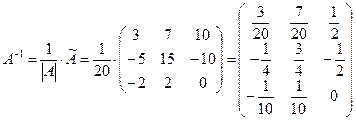 .
.
 .
.
Итак,  ,
,  ,
, 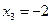 .
.
6. Решить систему линейных уравнений методом Гаусса:

Решение
Вычислим определитель системы:

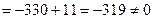 .
.
Следовательно, система совместна и имеет единственное решение.
Составим расширенную матрицу системы и приведем ее к треугольному виду.

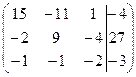 ~
~ +
+  +
+
 ~
~ ~
~ + ~
+ ~ .
.
Из полученной матрицы составим систему линейных уравнений и найдем неизвестные с помощью обратного хода Гаусса:
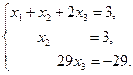 Отсюда:
Отсюда: 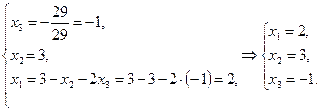
Ответ:  ,
, 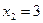 ,
, 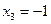 .
.
7. Решить систему линейных уравнений методом Жордановых исключений:
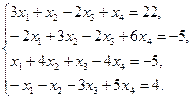
Решение
Составим таблицу коэффициентов системы и преобразуем ее так, чтобы на ее главной диагонали стояли только единицы, а все остальные элементы были равны нулю.
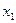
| 
| 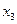
| 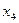
| 
|
| –2 | ||||
| –2 | –2 | –5 | ||
| –4 | –5 | |||
| –1 | –1 | –3 | ||
| 1/3 | –2/3 | 1/3 | 22/3 | |
| 11/3 | –10/3 | 20/3 | 29/3 | |
| 11/3 | 5/3 | –13/3 | –37/3 | |
| –2/3 | –11/3 | 16/3 | 34/3 | |
| –4/11 | –3/11 | 71/11 | ||
| –10/11 | 20/11 | 29/11 | ||
| –11 | –22 | |||
| –47/11 | 72/11 | 144/11 | ||
| –59/55 | 267/55 | |||
| –2/11 | –15/11 | |||
| –11/5 | –22/5 | |||
| –157/55 | –314/55 | |||
Из таблицы имеем:
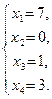
8. Найти общее решение и фундаментальную систему решений системы однородных линейных уравнений:
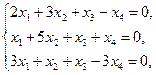
Решение
Запишем матрицу системы и преобразуем ее к ступенчатому виду:
 ~
~ ~
~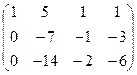 ~
~ .
.
Ранг матрицы равен 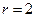 , значит фундаментальная система решений состоит из
, значит фундаментальная система решений состоит из  решений. Перепишем преобразованную систему:
решений. Перепишем преобразованную систему:
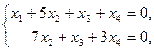
где 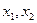 – базисные неизвестные,
– базисные неизвестные, 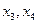 – свободные неизвестные.
– свободные неизвестные.
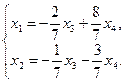
Введем обозначения 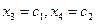 и запишем общее решение системы:
и запишем общее решение системы:
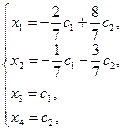
где 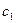 и
и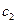 – произвольные постоянные.
– произвольные постоянные.
Придадим произвольным постоянным 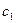 и
и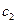 последовательно значения
последовательно значения  и
и  соответственно, получим:
соответственно, получим:
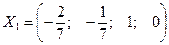 и
и 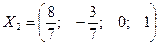 – фундаментальная система решений.
– фундаментальная система решений.
9. Найти матрицу линейного оператора A в базисе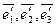 , если в стандартном базисе
, если в стандартном базисе матрица линейного оператора А имеет вид:
матрица линейного оператора А имеет вид:
 .
.
Решение
Матрицы 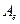 и
и  линейного оператора A связаны соотношением
линейного оператора A связаны соотношением  , где C – матрица перехода от базиса
, где C – матрица перехода от базиса 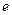 к базису
к базису 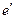 , она имеет вид:
, она имеет вид:
 ,
, 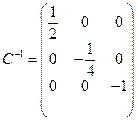 .
.
Подставим матрицы 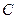 ,
, 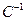 ,
, 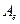 в соотношение
в соотношение

 .
.
Итак,  .
.