рефераты конспекты курсовые дипломные лекции шпоры

  • Раздел Математика
  •  / 
  • Решение квадратных систем линейных алгебраических уравнений (СЛАУ) матричным методом и по правилу Крамера

Реферат Курсовая Конспект

Решение квадратных систем линейных алгебраических уравнений (СЛАУ) матричным методом и по правилу Крамера

Решение квадратных систем линейных алгебраических уравнений (СЛАУ) матричным методом и по правилу Крамера - раздел Математика, ВВЕДЕНИЕ В ЛИНЕЙНУЮ АЛГЕБРУ. КРАТКИЙ ОБЗОР   Пусть Задана Система Вида: ...

 

Пусть задана система вида:

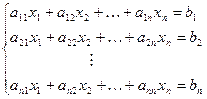
(11)

Запишем квадратную матрицу системы размерности :

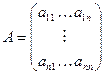, матрицу-столбец из неизвестных 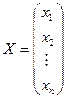, и матрицу-столбец из свободных коэффициентов .

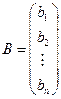В этих обозначениях система (11) примет вид:

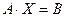. (12)

Если , то решение матричного уравнения (12) следующее:

. (13)

Заметим, что , т.е. 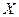– матрица такой же размерности, что и . Формула для обратной матрицы .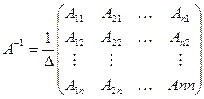

Решение:

.

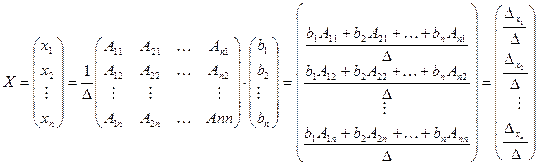Тем самым мы получили формулы Крамера:

. (14)

для СЛАУ (11), где главный определитель системы , а – вспомогательные определители (получающиеся из главного заменой -го столбца на столбец из свободных коэффициентов). Например

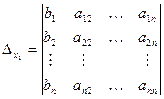можно обозначить .

 

Развернуть
Открыть в широком формате

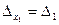– Конец работы –

Эта тема принадлежит разделу:

ВВЕДЕНИЕ В ЛИНЕЙНУЮ АЛГЕБРУ. КРАТКИЙ ОБЗОР

Матрицы Начальные сведения Рассматриваем новый математический объект... Операции над матрицами...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение квадратных систем линейных алгебраических уравнений (СЛАУ) матричным методом и по правилу Крамера

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Матрицы. Начальные сведения
  Рассматриваем новый математический объект – матрицу. Это абстрактная таблица, состоящая из

Определители квадратных матриц
  Прежде чем ввести операцию обращения матриц , необходимо дать понятие определителя квадр

Нахождение обратной матрицы
  Теперь можно перейти к обращению квадратных матриц. В этом случае должен быть отличным от нуля,

Решение матричных уравнений
  Пусть задано уравнение , (8) &nb

Теорема 1 (Крамера).
СЛАУ (11) можно привести к виду: . (15) Тогда во

Метод Жордановых исключений
  В основе метода Жордановых исключений лежат элементарные преобразования типа Гаусса, с помощью которых приводим матрицу системы к единичной

II. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
  2.1. n–мерные векторные пространства   Упорядоченная совокупность

Собственные векторы и собственные значения
  Вектор называется собственным вектором линейного оператора

Приведение квадратичной формы к каноническому виду
  Пусть задана квадратичная форма от двух переменных вида: , где

III. ОБРАЗЕЦ ВЫПОЛНЕНИЯ ТИПОВОГО РАСЧЕТА
  1. Вычислить определитель четвертого порядка с помощью свойств определителей:

Вычислить определитель четвертого порядка с помощью свойств определителей
  1. 2.

Найти обратную матрицу и сделать проверку
  1. 2.

Решить матричное уравнение
  1. 2.

Решить систему линейных уравнений методом Крамера
  1. 2.

Решить систему линейных уравнений матричным методом
  1. 2.

Решить систему линейных уравнений методом Гаусса
  1. 2.

Решить систему линейных уравнений методом Жордановых исключений
  1. 2.

Хотите получать на электронную почту самые свежие новости?
Education Insider Sample
Подпишитесь на Нашу рассылку
Наша политика приватности обеспечивает 100% безопасность и анонимность Ваших E-Mail
Реклама
Соответствующий теме материал
  • Похожее
  • Популярное
  • Облако тегов
  • Здесь
  • Временно
  • Пусто
Теги