рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Закон инерции квадратичных форм
Реферат Курсовая Конспект
Закон инерции квадратичных форм
Закон инерции квадратичных форм - раздел Математика, ЛИНЕЙНАЯ АЛГЕБРА Квадратичную Форму Можно Приводить К Нормальному Виду Различными Невырожденны...
Квадратичную форму можно приводить к нормальному виду различными невырожденными линейными преобразованиями (преобразованиями координат). Возникает вопрос: как связаны между собой различные нормальные виды одной и той же квадратичной формы.
Пусть Ln – n-мерное линейное пространство над полем Р и пусть на нём задана квадратичная форма j(а). Пусть в Ln задан базис е = (е1, е2,… , еn) и пусть А – матрица данной формы в этом базисе. Пусть е1 = (е11, е21,… , еn1) – один из базисов, в котором j(а) имеет канонический вид, и Т матрица перехода от базиса е к базису е1. В базисе е1 форма j(а) имеет диагональную матрицу А1. По формуле (56) А1 = ТТ×А×Т. Матрицы Т и ТТ невырожденные. Умножение матрицы А на невырожденную матрицу не меняет ранга матрицы А, следовательно, rang A = rang A1, т.е. в любом базисе матрица квадратичной формы имеет один и тот же ранг.
Определение 63. Рангом квадратичной формы, заданной на линейном пространстве Ln называется ранг её матрицы в любом базисе этого пространства.
Так как ранг диагональной матрицы равен числу отличных от нуля диагональных элементов, то любой канонический вид данной квадратичной формы содержит одно и тоже число квадратов переменных с ненулевыми коэффициентами. Это число равно рангу формы. Следовательно, доказано утверждение :
Теорема 66. Комплексная квадратичная форма любым невырожденным линейным преобразованием приводится к одному и тому же нормальному виду, состоящему из r квадратов переменных с единичными коэффициентами, т.е. j = х12 + х22 + … + хr2.
Если поле Р есть поле действительных чисел, то нормальный вид квадратичной формы будет j(а) = х12 + х22 + … + хк2 – хк+12 – … – хr2.
Определение 64. Число квадратов переменных, входящих с коэффициентом (+1) в нормальный вид действительной квадратичной формы, называется положительным индексом инерции этой формы. Число квадратов с коэффициентом (–1) называется отрицательным индексом инерции, разность между числом переменных и рангом квадратичной формы (т.е. n – r) называется её дефектом.
Теорема 67 (закон инерции квадратичных форм). Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится квадратичная форма с действительными коэффициентами действительным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.
Доказательство. Пусть j(а) – квадратичная форма, заданная в базисе е = (е1, е2,… , еn) линейного пространства Ln над полем R, а = х1е1 + х2е2 + … + хnеn. Пусть эта форма приведена двумя способами к двум нормальным видам. Согласно предыдущим результатам оба этих нормальных вида содержат одинаковое число квадратов переменных с ненулевыми коэффициентами. Пусть
j = у12 + у22 + … + ук2 – ук+12 – … – уr2 =
= z12 + z22 + … + zр2 – zр+12 – … – zr2. (*)
Пусть уі = 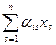 , і = 1, 2, … , n (**), и zј =
, і = 1, 2, … , n (**), и zј = 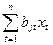 , ј = 1, 2, … , n (***).
, ј = 1, 2, … , n (***).
Так как эти формулы задают невырожденные преобразования, то их определители отличны от нуля. Достаточно доказать, что к = р. Предположим, что к ¹ р. Не нарушая общности, можно считать, что к < р. Составим систему уравнений у1 = у2 = … = ук = zр+1 = … = zr = zr+1 = … = zn = 0. Это система n – р + к линейных однородных уравнений от n неизвестных. Так как число уравнений меньше числа неизвестных, то она имеет ненулевые решения. Пусть (х10, х20, … , хn 0 ) – одно из них. Подставив это решение в формулы (**) и (***), вычислим все уі и zј и подставим их в равенство (*). Получим –(ук+10)2 – … – (уr0)2 = (z10)2 + (z20)2 + … + (zр0)2. Это равенство возможно тогда и только тогда, когда ук+10 = … = уr0 = z10 = z20 = … = zр0 = 0. Получили, что система z1 = z2 = … = zр = zр+1 = … = zr = zr+1 = … = zn = 0 имеет ненулевое решение (х10, х20, … , хn 0 ), что невозможно, т.к. ранг этой системы равен n. Итак, наше предположение не верно. Следовательно, к = р.
9.5. Положительно определённые квадратичные формы
Определение 65. Действительная квадратичная форма называется положительно определённой, если для любого вектора а ¹ 0 имеет место j(а) > 0.
Теорема 68. Действительная квадратичная форма является положительно определённой тогда и только тогда, когда её ранг и положительный индекс инерции равны числу неизвестных.
Доказательство. Þ Пусть j(а) – действительная положительно определённая квадратичная форма. Пусть она приводится к нормальному виду
у12 + у22 + … + ук2 – ук+12 – … – уr2 (*),
в котором либо r < n, либо r = n, но к < n. Пусть преобразование координат, с помощью которого форма приведена к нормальному виду, задаётся формулами уі = 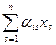 (**). Определитель этих формул отличен от нуля. Если r < n, то возьмём у1 = у2 = … = уn–1 = 0, уn = 1 и подставим в (**). Получим систему n линейных неоднородных уравнений с n неизвестными и с определителем, отличным от нуля. По правилу Крамера эта система имеет единственное решение. Очевидно, это решение не нулевое, поэтому определяет ненулевой вектор а. Но тогда j(а) = 0, что противоречит определению положительно определённой формы. Аналогично приходим к противоречию и в случае r = n, но к < n. Итак, если форма положительно определённая, то её нормальный вид у12 + у22 + … + уn2. Это и значит, что ранг и положительный индекс инерции равны n.
(**). Определитель этих формул отличен от нуля. Если r < n, то возьмём у1 = у2 = … = уn–1 = 0, уn = 1 и подставим в (**). Получим систему n линейных неоднородных уравнений с n неизвестными и с определителем, отличным от нуля. По правилу Крамера эта система имеет единственное решение. Очевидно, это решение не нулевое, поэтому определяет ненулевой вектор а. Но тогда j(а) = 0, что противоречит определению положительно определённой формы. Аналогично приходим к противоречию и в случае r = n, но к < n. Итак, если форма положительно определённая, то её нормальный вид у12 + у22 + … + уn2. Это и значит, что ранг и положительный индекс инерции равны n.
Ü Ранг и положительный индекс инерции действительной квадратичной формы равны n. Докажите самостоятельно, что форма положительно определённая.
Отметим без доказательства ещё одну теорему о положительно определённых действительных квадратичных формах.
Теорема 69. Действительная квадратичная форма является положительно определённой тогда и только тогда, когда все главные миноры её матрицы положительны.
Теорема 70. Квадрат длины вектора в любом базисе евклидова пространства задаётся положительно определённой квадратичной формой.
Доказательство. Пусть Еn – n-мерное евклидово пространство, е = (е1, е2,… , еn) – базис в нём и Г – матрица Грама, задающая скалярное произведение векторов в этом базисе. Если а = х1е1 + х2е2 + … + хnеn , в = у1е1+ у2е2 + … + уnеn, то (а, в)= х Т×Г×у, где х Т– строка координат вектора а, у – столбец координат вектора в. Следовательно, а2 = (а, а) = х Т×Г×х. Если сравнить с формулой (60), то получим, что х Т×Г×х есть квадратичная форма с матрицей Г. В пространстве Еn есть ортонормированный базис. В этом базисе а2 = х12 + х22 +…+ хn2. Но это значит, что при переходе к ортонормированному базису квадратичная форма х Т×Г×х приводится к нормальному виду х12 + х22 +…+ хn2. По теореме 68 получаем, что форма х Т×Г×х является положительно определённой.
Пример. Какие из следующих квадратичных форм являются положительно определёнными?
1. 4х12 – х1х2 + 3х22 – х2х3 + 6х2х4.
2. 4х1х2 – х1х3 + 2х22 – 4х2х3 + 3х2х4 + 5х42.
3. 4х12 – 5х1х2 + 3х22 – 2х2х3 + х32 + 4х2х4 – х42 .
Решение. Ответить на вопрос можно двумя способами: привести форму к каноническому виду или вычислить главные миноры матрицы данной формы. Для первой формы используем первый способ, для второй и третьей – второй способ.
1. 4х12 – х1х2 + 3х22 – х2х3 + 6х2х4 = (4х12 – х1х2 +  ) –
) –  + 3х22 – х2х3 + 6х2х4 =
+ 3х22 – х2х3 + 6х2х4 =
= (2х1–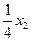 )2 +
)2 + 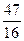 ( х22
( х22  –
–
 = (2х1–
= (2х1–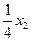 )2 +
)2 + 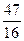 (
( –
– 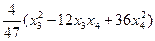 =
=
= (2х1–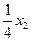 )2 +
)2 + 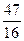 (
( –
– 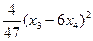 . Отсюда следует, что ранг данной формы равен 3, т.е. меньше числа переменных, поэтому эта форма не является положительно определённой (теорема 68).
. Отсюда следует, что ранг данной формы равен 3, т.е. меньше числа переменных, поэтому эта форма не является положительно определённой (теорема 68).
2. Составим матрицу второй квадратичной формы и найдём главные её миноры.
А = 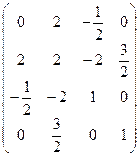 , М1 = 0. Уже отсюда следует, что форма не является положительно определённой (теорема 69).
, М1 = 0. Уже отсюда следует, что форма не является положительно определённой (теорема 69).
3. Составим матрицу третьей квадратичной формы и найдём главные её миноры.
А = 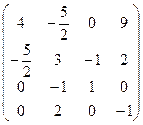 , М1 = 4 > 0, М2 =
, М1 = 4 > 0, М2 = 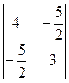 = 5,75 > 0, М3 =
= 5,75 > 0, М3 = 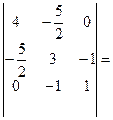 1,25 > 0,
1,25 > 0,
М4 = ½А½= 14,25 > 0. Итак, все главные миноры положительны. Следовательно, третья квадратичная форма положительно определённая.
– Конец работы –
Эта тема принадлежит разделу:
ЛИНЕЙНАЯ АЛГЕБРА
З И Андреева... ЛИНЕЙНАЯ АЛГЕБРА...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Закон инерции квадратичных форм
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов