Базисы в пространствах .
Система векторов 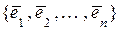 называется базисом пространства
называется базисом пространства 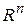 , если любой вектор
, если любой вектор  может быть единственным образом представлен в виде линейной комбинации векторов этой системы:
может быть единственным образом представлен в виде линейной комбинации векторов этой системы:
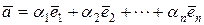 .
.
Числа 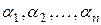 называют коэффициентами разложения вектора
называют коэффициентами разложения вектора  по базису
по базису 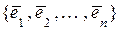 .
.
В пространстве  примером базиса может служить система единичных ортов:
примером базиса может служить система единичных ортов: 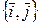 . Данный базис принято называть естественным, т.к. коэффициентами разложения любого вектора
. Данный базис принято называть естественным, т.к. коэффициентами разложения любого вектора  по базису
по базису 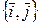 являются координаты этого вектора. Например,
являются координаты этого вектора. Например, 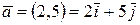 .
.
В пространстве 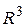 естественный базис образует система векторов
естественный базис образует система векторов  .
.
Теорема 5. Если система векторов образуют базис в  , то она линейно независима.
, то она линейно независима.
Теорема 6. Любые 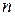 линейно независимых векторов пространства
линейно независимых векторов пространства  образуют в нем базис.
образуют в нем базис.
Пример 3. (Образец решения задачи 3 из контрольной работы). Даны векторы 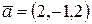 ,
,  ,
,  . Определить образуют ли векторы
. Определить образуют ли векторы  ,
, 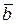 и
и  базис в пространстве
базис в пространстве 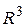 и если да, то разложить вектор
и если да, то разложить вектор  по этому базису.
по этому базису.
Решение. Составим определитель из векторов  ,
, 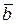 и
и  :
:
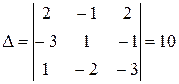
Т.к. 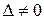 , то система
, то система 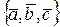 - линейно независима и по теореме 12 образует базис в пространстве
- линейно независима и по теореме 12 образует базис в пространстве 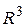 . Значит, вектор
. Значит, вектор  может быть единственным образом представлен в виде:
может быть единственным образом представлен в виде:

с пока неизвестными коэффициентами 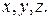 Переходя от равенства векторов к равенству их соответствующих координат приходим к системе линейных уравнений:
Переходя от равенства векторов к равенству их соответствующих координат приходим к системе линейных уравнений:
 ,
,
откуда:
 .
.
Решая эту систему, например, методом Крамера (сделайте это самостоятельно), получим: 
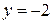 ,
, 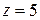 . Следовательно,
. Следовательно,
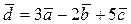 .n
.n