рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Реферат Курсовая Конспект
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ - раздел Математика, Темы: Линейная Алгебра...
Темы:
ЛИНЕЙНАЯ АЛГЕБРА
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
АЛГЕБРА МАТРИЦ. ДЕЙСТВИЯ НАД МАТРИЦАМИ
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ
ОПРЕДЕЛИТЕЛИ
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
РАНГ МАТРИЦЫ
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ. ТЕОРЕМА КРОНИКЕРА-КАПЕЛЛИ
РЕШЕНИЯ НЕВЫРОЖДЕННЫХ ЛИНЕЙНЫХ СИСТЕМ ФОРМУЛОЙ КРАМЕРА
РЕШЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА
СИСТЕМА ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ
ОСНОВНЫЕ СВОЙСТВА ПРОЕКЦИЙ
РАЗЛОЖЕНИЕ ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ
РАВЕНСТВО ВЕКТОРОВ
КОЛЛИНЕАРНОСТЬ ВЕКТОРОВ
КООРДИНАТЫ ВЕКТОРА
КООРДИНАТЫ ТОЧКИ
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ВЫРАЖЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ СОМНОЖИТЕЛЕЙ
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
27. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЁХ ВЕКТОРОВ
СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
ВЫРАЖЕНИЕ СМЕШАННОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КООРДИНАТЫ
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
31. РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ВЕКТОРНАЯ АЛГЕБРА».
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ НА ПЛОСКОСТИ
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ОСЕЙ КООРДИНАТ
ПОВОРОТ ОСЕЙ КООРДИНАТ
ЛИНИИ НА ПЛОСКОСТИ (ОСНОВНЫЕ ПОНЯТИЯ)
УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. ОСНОВНЫЕ ЗАДАЧИ
ВОПРОСЫ К ЭКЗАМЕНУ
ЛИНЕЙНАЯ АЛГЕБРА
Матрицей, называется прямоугольная таблица чисел, содержащая m-строк…Векторы. Основные понятия.
Величины, которые полностью определены своим численным значением, называются скалярными. Другие величины, которые определены не только своим числовым значением, но и направлением, называются векторные. Векторная величина геометрически изображается с помощью вектора.
Вектор – это направленный прямолинейный отрезок, т.е. отрезок имеющий определенную длину и определенное направление. Если Ā начало вектора, а 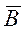 его конец, то вектор обозначается символом
его конец, то вектор обозначается символом  или
или 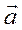 . Вектор
. Вектор 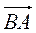 , называется противоположным вектору
, называется противоположным вектору 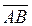 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , обозначается -
, обозначается - .
.
Длиной или модулем вектора 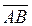 , называется длина отрезка и обозначается
, называется длина отрезка и обозначается 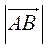 . Вектор длина, которого равняется нулю, называется нулевым и обозначается, как
. Вектор длина, которого равняется нулю, называется нулевым и обозначается, как 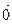 (нулевой вектор направления не имеет). Вектор длина, которого равна единице, называется единичным вектором и обозначается
(нулевой вектор направления не имеет). Вектор длина, которого равна единице, называется единичным вектором и обозначается 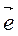 . Единичный вектор направление, которого совпадает с вектором
. Единичный вектор направление, которого совпадает с вектором  , называется ортом вектора
, называется ортом вектора  и обозначается
и обозначается 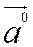 . Вектора
. Вектора  и
и 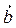 , называются коллинеарными, если они лежат на одной прямой или на параллельных прямых и обозначается
, называются коллинеарными, если они лежат на одной прямой или на параллельных прямых и обозначается  ║
║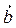 . Коллинеарные вектора могут быть направлены одинаково ↑↑ или противоположно ↓↑ в одну сторону или со направлены в разные стороны. Нулевой вектор считается коллинеарным любому вектору. Два вектора
. Коллинеарные вектора могут быть направлены одинаково ↑↑ или противоположно ↓↑ в одну сторону или со направлены в разные стороны. Нулевой вектор считается коллинеарным любому вектору. Два вектора  и
и 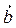 , называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины, т.е. вектора равны, если равны их модули и совпадает направление.
, называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины, т.е. вектора равны, если равны их модули и совпадает направление.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространств, т.е. свободный вектор.
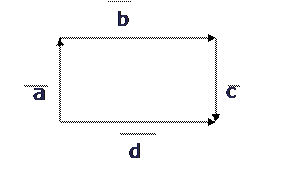
На рисунке векторы образуют прямоугольник, причем 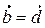 , а вектор
, а вектор  (вектора
(вектора  и
и 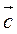 противоположные).
противоположные).
Три вектора в пространстве, называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов, хотя бы один нулевой или два любые коллинеарны, то такие вектора компланарны.
Вектора бывают:
1. свободный – это такой вектор, который переносится параллельно самому себе в пространстве. Характеризуется модулем и направлением. Точка начала вектора может быть любая точка в пространстве
2. скользящий – это вектор расположен на линии скольжения или действия. Характеризуется направлением и модулем. Точка начала вектора может быть любая точка на линии принадлежащая линии
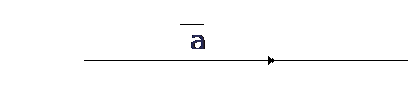
3. связанный – это вектор точка начала вектора является фиксированной. Сам вектор характеризуется направлением и модулем.
Угол между векторами, называется наименьшим. Угол между векторами, имеющий общую точку начала

Угол между вектором и осью. Ось – это прямая с выбранным положительным направлением.
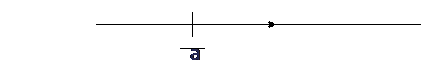
Угол между заданным вектором и осью, называется угол между заданным вектором и орт вектором.

Линейные операции над векторами.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть  и
и 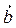 два произвольных вектора. Возьмем произвольную точку О и построим вектор
два произвольных вектора. Возьмем произвольную точку О и построим вектор 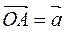 . От точки
. От точки  отложим вектор
отложим вектор  . Вектор
. Вектор  соединяет начало первого вектора с концом второго, называющийся суммой векторов
соединяет начало первого вектора с концом второго, называющийся суммой векторов  и
и 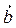 .
.
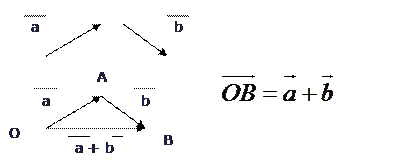
Это правило сложения векторов, называется правилом треугольника. Сумму двух векторов можно построить по правилу параллелограмма.
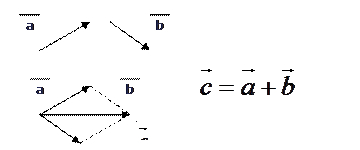
Сложение трех векторов 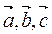 используем
используем

Под разностью векторов  и
и 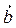 понимается вектор
понимается вектор  , такой что
, такой что 
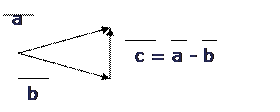
Отметим, что в параллелограмме построенном на векторах  и
и 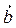 одна направленная диагональ является суммой векторов
одна направленная диагональ является суммой векторов  и
и 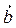 , а другая разностью.
, а другая разностью.

Можно вычитать по следующему правилу:
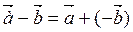 , т.е. вычитание векторов заменим – сложить вектор
, т.е. вычитание векторов заменим – сложить вектор  с противоположным вектору
с противоположным вектору 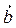 .
.
Произведение вектора  на скаляр или число λ, называется вектор λ*
на скаляр или число λ, называется вектор λ* или
или  * λ, который имеет длину
* λ, который имеет длину 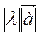 , коллинеарен вектору
, коллинеарен вектору  имеет направление вектора
имеет направление вектора  (λ > 0) и противоположное направление, если λ < 0
(λ > 0) и противоположное направление, если λ < 0

Из определения произведения вектора на число, следует свойство этого произведения:
1. если 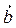 = λ*
= λ* , то
, то 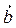 ║
║ . Наоборот, если
. Наоборот, если 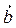 и
и  коллинеарны, причем
коллинеарны, причем  = 0, то при некотором λ верно равенство
= 0, то при некотором λ верно равенство 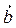 = λ*
= λ*
2. каждый вектор равен произведению его модуля на орт  =
=  *
*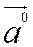
Свойство линейных операций над векторами:
1. 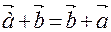
2. 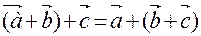
3. 
4. 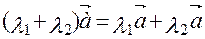
5. 
Эти свойства позволяют проводить преобразования в линейных операциях с векторами, т.к. это делается в обычной алгебре, а именно слагаемые менять местами, вводить скобки, группировать и выносить за скобки, как скаляры, так и векторные общие множители.
Тема: ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ
Выражение «проекция вектора  на ось ОХ» употребляется в двух разных смыслах: геометрическом и алгебраическом (арифметическом).
на ось ОХ» употребляется в двух разных смыслах: геометрическом и алгебраическом (арифметическом).
1. Проекцией (геометрической) вектора  на ось ОХ, называется вектор
на ось ОХ, называется вектор 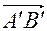 (рис 1) начало, которого А' есть проекция начала А на ось ОХ, а конец В' – проекция конца В на ту же ось.
(рис 1) начало, которого А' есть проекция начала А на ось ОХ, а конец В' – проекция конца В на ту же ось.

3. Связь между компонентой (геометрической проекцией) и алгебраической проекцией вектора. Пусть  есть вектор, равнонаправленный с осью ОХ и имеющий длину 1. Тогда геометрическая проекция (компонента) какого-либо вектора
есть вектор, равнонаправленный с осью ОХ и имеющий длину 1. Тогда геометрическая проекция (компонента) какого-либо вектора 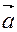 , по оси ОХ равна произведению вектора
, по оси ОХ равна произведению вектора  на алгебраическую проекцию вектора
на алгебраическую проекцию вектора 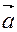 по той же оси:
по той же оси:
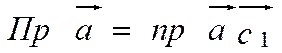
Пример 2. При обозначениях рис 2 имеем
 . Геометрическая проекция вектора
. Геометрическая проекция вектора 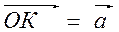 на ось ОХ есть вектор
на ось ОХ есть вектор  , алгебраическая проекция того же вектора есть число -2 (см пример 1). Имеем:
, алгебраическая проекция того же вектора есть число -2 (см пример 1). Имеем: 
Тема: ОСНОВНЫЕ СВОЙСТВА ПРОЕКЦИЙ
Если  , то
, то 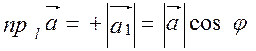
Если  (
(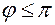 ), то
), то  (см рис 1)
(см рис 1)
Если , то
, то 
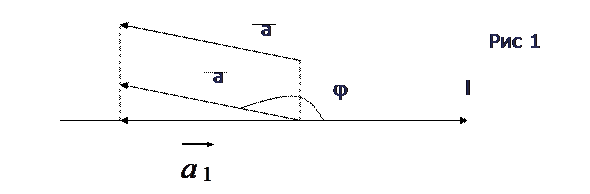
Свойство 1. Проекция вектора 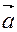 на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора 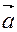 на cos угла φ медлу вектором и осью, т.е.
на cos угла φ медлу вектором и осью, т.е. 
Следствие 1.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
Следствие 1.2. Проекция равных векторов на одну и ту же ось равны между собой.
Пусть, например,  , имеем
, имеем  , т.е.
, т.е.  (см рис 2)
(см рис 2)
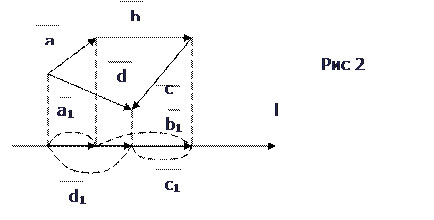
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
Свойство 3. При умножении вектора 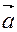 на число λ его проекция на ось также умножается на это число, т.е.
на число λ его проекция на ось также умножается на это число, т.е.  .
.
При λ > 0 имеем 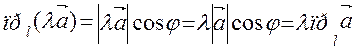 (свойство 1)
(свойство 1)
При λ < 0: 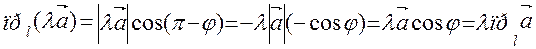
Свойство справедливо, очевидно, и при λ = 0.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Тема:РАЗЛОЖЕНИЕ ВЕКТОРА ПО ОРТАМ КООРДИНАТНЫХ ОСЕЙ
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях ОХ, ОУ и OZ единичные векторы (орты), обозначаемые i , j , k соответственно (см. рис. 3).
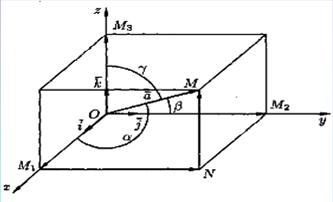
Рис.3
Выберем произвольный вектор 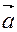 пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 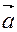 =
=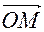 .
.
Найдем проекции вектора 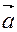 на координатной оси. Проведем через конец вектора
на координатной оси. Проведем через конец вектора 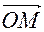 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через  ,
, 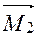 и
и 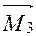 . Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 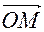 . Тогда
. Тогда 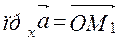 ,
,  ,
,  . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим 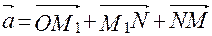 .
.
А так как 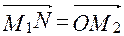 ,
,  , то
, то 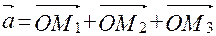 .
.
Обозначим проекции вектора 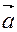 =
=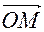 на оси ОХ, ОУ и OZ соответственно через
на оси ОХ, ОУ и OZ соответственно через 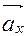 ,
,  и
и 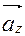 , т.е.
, т.е.  ,
, 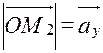 ,
,  . Тогда получаем:
. Тогда получаем:
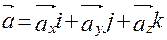
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа 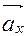 ,
,  ,
, 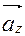 , называются координатами вектора
, называются координатами вектора 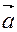 , т. е. координаты вектора есть его проекции на соответствующие координатные оси.
, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство часто записывают в символическом виде: 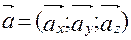 .
.
Равенство 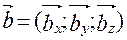 означает, что
означает, что  . Зная проекции вектора
. Зная проекции вектора 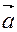 , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать  , т.е.
, т.е. 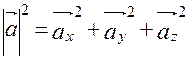


 т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора 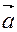 с осями ОХ, ОУ и OZ соответственно равны a,b,g. По свойству проекции вектора на ось, имеем
с осями ОХ, ОУ и OZ соответственно равны a,b,g. По свойству проекции вектора на ось, имеем  ,
, 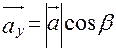 ,
, 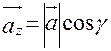 . Или, что, то же самое,
. Или, что, то же самое,  ,
, 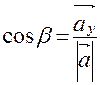 ,
,  . Числа cos α, cos β, cos γ , называются направляющими косинусами вектора
. Числа cos α, cos β, cos γ , называются направляющими косинусами вектора 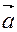 .
.
Подставим выражения  ,
, 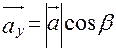 ,
, 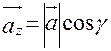 в равенство
в равенство ,получаем:
,получаем: 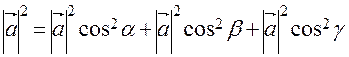
Сократив на 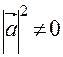 получим соотношение:
получим соотношение:  ,
,
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора 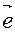 являются числа cos α, cos β, cos γ , т.е.
являются числа cos α, cos β, cos γ , т.е. 
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.
Модуль вектора.
Модуль вектора обозначается двумя вертикальными чертами – слева и справа: , или , или а. При двухбуквенном обозначении вектора его модуль иногда обозначается теми же…Действия над векторами, заданными проекциями.
, Тема: РАВЕНСТВО ВЕКТОРОВТеорема 1.
. Векторное произведение этих векторов имеет координаты .Геометрический смысл смешанного произведения
Теорема 2.
Если векторы – компланарны, то объем равен нулю, и . доказательство. Пусть S – площадь параллелограмма, построенного на векторах ,… Из геометрического свойства 2 векторного произведения:Следствие 1.
доказательство. Скалярное произведение векторов коммутативно, следовательно . По теореме 2: , .Следствие 2.
Тема: СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВТеорема 3.
. доказательство. . По теореме о векторном произведении:АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Под системой координат на плоскости понимают способ позволяющий, численно описать положение точки плоскости. Одной из таких систем является,… Оси координат делят плоскость на 4 области – четверти или квадрантыПреобразование системы координат.
Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами…Рис 13. Полукубическая парабола
Уравнение кривой у2 = х3 или

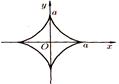
Рис. 14. Астроида
Уравнение в прямоугольных координатах: х2/3+y2/3 =а2/3; параметрические уравнения:


Рис. 15. Кардиоида
Уравнение в полярных координатах мест вид r = а(1+ cosφ), где а > 0. Кардиоида — частный случай улитки Паскаля (а = b).

Рис. 16. Спираль Архимеда
Уравнение кривой в полярных координатах r = а φ ,где а > 0— постоянное.
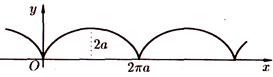
Рис. 17. Циклоида
Параметрические уравнения циклоиды имеют вид

Циклоида — это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой.
Тема: УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.
 Уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом
Пусть на плоскости Оху задана произвольная прямая, не параллельная оси Оу. Ее положение вполне определяется ординатой b точки N(0;b) пересечения с осью Оу и углом α между осью Ох и прямой (см. рис. 18).
Под углом α (0≤ α < π) наклона прямой
рис. 18 понимается наименьший угол на который нужно повернуть вокруг точки пересечения прямой и оси Оx против часовой стрелки ось Ох до ее совпадения с прямой.
Возьмем на прямой произвольную точку М(х;у) (см. рис. 18). Проведем через точку N ось Nx', параллельную оси Ох и одинаково с ней направленную
Угол между осью Nx'. и прямой равен а. В системе Nx'y точка М имеет координаты х и у-b.
Из определения тангенса угла следует равенство
| tga= | у-b |
| х |
, т. е. у = tga*x + b. Введем обозначение tga = k, получаем уравнение у = кх + b, (2.2)
которому удовлетворяют координаты любой точки М(х;у) прямой
Можно убедиться, что координаты любой точки Р(х;у), лежащей вне данной прямой, уравнению (2.2) не удовлетворяют.
Число к = tga называется угловым коэффициентом прямой, а уравнение (2.2) — уравнением прямой с угловым коэффициентом.
Если прямая проходит через начало координат, то b = 0 и, следовательно, уравнение этой прямой будет иметь вид у = кх.
Если прямая параллельна оси Ох, то a = 0, следовательно, к =tga = 0 и уравнение (2.2) примет вид у = b. Если прямая параллельна оси Оу, то a =π/2, уравнение (2.2) теряет смысл, т. к. для нее угловой коэффициент к = tga = tg π/2 не существует. В этом случае уравнение прямой будет иметь вид
х = а, (2.3)
а- абсцисса точки пересечения прямой с осью Ох. Отметим, что уравнения (2.2) и (2.3) есть уравнения первой степени.
Общее уравнение прямой
Ах + Ву + С = 0, (2.4) где А, В, С — произвольные числа, причем А и В не равны нулю одновременно. Покажем, что уравнение (2.4) есть уравнение прямой линии. Возможны два случая.Уравнение прямой, проходящей через данную точку в данном направлении
Подставляя значение b в уравнение у = кх + b, получим искомое уравнение прямой у = кх + уо - кхо, т. е. у - у о = к(х-хо). (2.5) Уравнение (2.5) с различными значениями к называют также уравнениями пучка прямых с центром в точке М(хо;уо)- Из этого…Уравнение прямой, проходящей через две точки
у –у1 = к(х-х1). (2.6) где к — пока неизвестный коэффициент. Так как прямая проходит через точку М2(х2;у2), то координаты этой точки должны удовлетворять уравнению (2.6): у2 - у 1…Уравнение прямой в отрезках
рис.19Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Возьмем на прямой произвольную точку М(х;у) и рассмотрим вектор = (х — хо;у — уо) (см. рис. 20). Поскольку векторы п и перпендикулярны, то их… А(х - х0) + В (у - уо) = 0. (2.8) Уравнение (2.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.Нормальное уравнение прямой
r•cos(φ - α) - р = 0, т. е. r•cosφ•cosα + r•sinφ•sinα- р = 0. Но, в силу формул, связывающих прямоугольные и полярные координаты, имеем:… r•sinφ = у. Следовательно, уравнение (2.10) прямой в прямоугольной системе координат примет видУгол между двумя прямыми и условия параллельности перпендикулярности двух прямых
у = к1х + b1 и у = к2х + b2 (см. рис. 22). Требуется найти угол φ, на который надо повернуть в положительном… Решение: Имеем α2 = φ + α1 (теорема и внешнем угле треугольника) или φ = α2 - α1. Если…– Конец работы –
Используемые теги: Элементы, ной, алгебры0.046
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов