Действия над комплексными числами в тригонометрической форме
Сложение и вычитание удобнее производить над комплексными числами в алгебраической форме, а умножение и деление – в тригонометрической форме.
1. Умножений.Пусть даны два комплексных числа, записанных в тригонометрической форме: z1 = r1(cosj1 + i×sinj1) z2 = r2(cosj2 + i×sinj2).
z1×z2 = r1×r2(cosj1×cosj2 – sinj1×sinj2) + i×(cosj1×sinj2 + sinj1×cosj2) = = r1×r2(cos(j1 + j2) + i×sin(j1 + j2)).
Итак, модуль |z1×z2| = r1×r2, аргумент arg(z1×z2) = arg z1 + arg z2.
Пример 1.13.Для z1 = 2(cos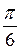
+ i×sin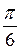) и z2 = 3(cos
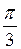+ i×sin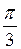) найти их произведение z1×z2.
Решение. Применяем формулу для нахождения произведения двух комплексных чисел, записанных в тригонометрической форме. z1×z2 = 2×3(cos(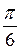 + 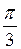) + i×sin( 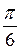+ 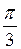)) = 6(cos
+ i×sin) – тригонометрическая форма произведения чисел z1 и z2 или в алгебраической форме z1×z2 = 6i.
2. Деление.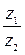 
= 
= 
×
=
= ×
=
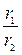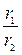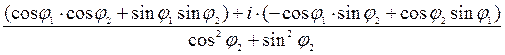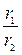= ×( cos(j1 – j2) + i×sin(j1 – j2))
Итак, модуль |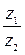| = 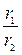, аргумент arg(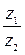) = arg z1 – arg z2.
Пример 1.14.Для z1 = 10(cos45° + i×sin45°) и z2 = 5(cos60° + i×sin60°) найти их частное от деления .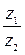
Решение.
= 
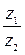(cos(45° – 60°) + i×sin(45° – 60°)) = 2(cos(–15°) + i×sin(–15°)) – тригонометрическая форма частного чисел z1 и z2. Заметим, что если данное выражение записать в виде равносильного выражения
2(cos15° – i×sin15°), то это не будет уже тригонометрической формой записи комплексного числа.