Возведение в степень.
Если z = r(cosj + i×sinj), то zn = rn(cos(nj) + i×sin(nj)), где n Î Z. Данная формула называется формулой Муавра[9].
Пример 1.15.Для z = 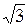 – i, найти z4.
– i, найти z4.
Решение. Воспользуемся формулой Муавра, но для начала надо это комплексное число записать в тригонометрической форме. В примере 1.12 мы это уже находили z = 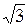 – i = 2(cos
– i = 2(cos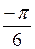 + i×sin
+ i×sin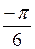 ). Тогда
). Тогда
z4 = (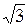 – i)4 = (2(cos
– i)4 = (2(cos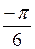 + i×sin
+ i×sin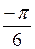 ))4 = 24(cos
))4 = 24(cos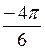 + i×sin
+ i×sin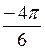 ) =
) =
= 16(cos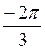 + i×sin
+ i×sin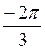 ) – тригонометрическая форма результата возведения в четвертую степень данного комплексного числа. Найдем также и алгебраическую форму записи числа z4. z4 = 16(cos
) – тригонометрическая форма результата возведения в четвертую степень данного комплексного числа. Найдем также и алгебраическую форму записи числа z4. z4 = 16(cos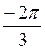 + i×sin
+ i×sin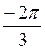 ) = 16(cos
) = 16(cos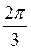 – i×sin
– i×sin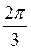 ) = 16(
) = 16(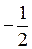 – i×
– i×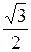 ) =
) =
= –8 – 8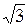 ×i.
×i.
4. Извлечение корня n-ой степени.
Можно показать, что каждое комплексное число, отличное от нуля, имеет ровно n корней n-й степени.
Если z = r(cosj + i×sinj), то
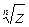 =
= 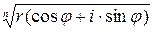 =
=
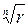 (cos
(cos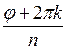 + i×sin
+ i×sin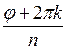 ), где k = 0, 1, …, n – 1.
), где k = 0, 1, …, n – 1.
Пример 1.16. Найти 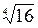 .
.
Решение. Пусть z = 16, найдем сначала тригонометрическую форму данного комплексного числа. Имеем z = 16 Þ a = 16, b = 0 Þ r = 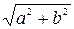 =
= 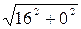 = 16; т. к. a = 16 > 0, то j =
= 16; т. к. a = 16 > 0, то j = 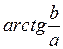 =
= 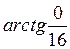 = =
= = 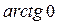 = 0. Тогда z = 16 = r(cosj + i×sinj) = 16(cos0 + i×sin0).
= 0. Тогда z = 16 = r(cosj + i×sinj) = 16(cos0 + i×sin0).
Применяем формулу для нахождения корня n-ой степени.
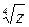 =
= 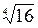 =
= 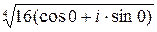 =
= 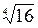 (cos
(cos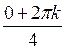 + i×sin
+ i×sin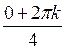 ) =
) =
= 2(cos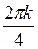 + i×sin
+ i×sin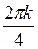 ) , где k = 0, 1, 2, 3. Найдем все четыре корня:
) , где k = 0, 1, 2, 3. Найдем все четыре корня:
k = 0 Þ w0 = 2(cos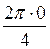 + i×sin
+ i×sin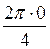 ) = 2 (cos0 + i×sin0) = 2,
) = 2 (cos0 + i×sin0) = 2,
k = 1 Þ w1 = 2(cos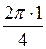 + i×sin
+ i×sin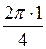 ) = 2(cos
) = 2(cos + i×sin
+ i×sin ) = 2(0 + i×1) = 2i,
) = 2(0 + i×1) = 2i,
k = 2 Þ w2 = 2(cos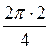 + i×sin
+ i×sin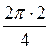 ) = 2(cosp + i×sinp) = 2(–1 + i×0) = –2,
) = 2(cosp + i×sinp) = 2(–1 + i×0) = –2,
k = 3 Þ w3 = 2(cos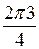 + i×sin
+ i×sin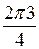 ) = 2(cos
) = 2(cos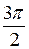 + i×sin
+ i×sin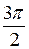 ) = 2(0 – i)) = –2i.
) = 2(0 – i)) = –2i.
Замечание. Геометрически все n значений корней n-ой степени из комплексного числа r(cosj + i×sinj) изображаются точками, лежащими на окружности с центром в начале координат, радиус которой равен 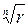 . Если эти точки соединить, то в результате получится правильный n-угольник.
. Если эти точки соединить, то в результате получится правильный n-угольник.