Фундаментальный набор решений однородной системы линейных уравнений
Пусть М0 – множество решений однородной системы (4) линейных уравнений.
Определение 6.12.Векторы с1, с2, …, сp, являющиеся решениями однородной системы линейных уравнений называются фундаментальным набором решений (сокращенно ФНР), если
1) векторы с1, с2, …, сp линейно независимы (т. е. ни один из них нельзя выразить через другие);
2) любое другое решение однородной системы линейных уравнений можно выразить через решения с1, с2, …, сp.
Заметим, что если с1, с2, …, сp – какой-либо ф.н.р., то выражением k1×с1 + k2×с2 + … + kp×сp можно описать все множество М0 решений системы (4), поэтому его называют общим видом решения системы (4).
Теорема 6.6. Любая неопределенная однородная система линейных уравнений обладает фундаментальным набором решений.
Способ нахождения фундаментального набора решений состоит в следующем:
• найти общее решение однородной системы линейных уравнений;
• построить (n – r) частных решений этой системы, при этом значения свободных неизвестных должны образовывать единичную матрицу;
• выписать общий вид решения, входящего в М0.
Пример 6.5. Найти фундаментальный набор решений следующей системы: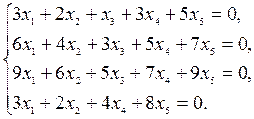 
Решение. Найдем общее решение этой системы.
~ 
~ 
~ ~ 
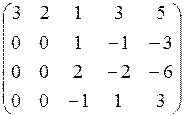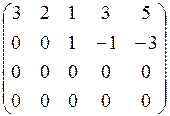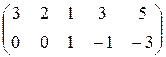Þ 
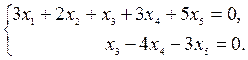Þ Þ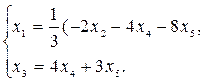 
В этой системе пять неизвестных (n = 5), из них главных неизвестных два (r = 2), свободных неизвестных три (n – r), то есть в фундаментальном наборе решений содержится три вектора решения. Построим их. Имеем x1 и x3 – главные неизвестные, x2, x4, x5 – свободные неизвестные
| x1 | x2 | x3 | x4 | x5 | |
| с1 |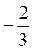 
| ||||
| с2 | 
| ||||
| с3 | 
|
Значения свободных неизвестных x2, x4, x5 образуют единичную матрицу E третьего порядка. Получили, что векторы с1, с2, с3 образуют ф.н.р. данной системы. Тогда множество решений данной однородной системы будет М0 = {k1×с1 + k2×с2 + k3×с3, k1, k2, k3 Î R}.
Выясним теперь условия существования ненулевых решений однородной системы линейных уравнений, другими словами условия существования фундаментального набора решений.
Однородная система линейных уравнений имеет ненулевые решения, то есть является неопределенной, если
1) ранг основной матрицы системы меньше числа неизвестных;
2) в однородной системе линейных уравнений число уравнений меньше числа неизвестных;
3) если в однородной системе линейных уравнений число уравнений равно числу неизвестных, и определитель основной матрицы равен нулю (т. е. |A| = 0).
Пример 6.6. При каком значении параметра a однородная система линейных уравнений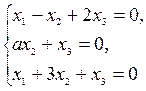 
имеет ненулевые решения?
Решение. Составим основную матрицу этой системы и найдем ее определитель: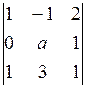 
= 
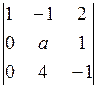= 1×(–1)1+1×
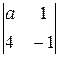= –а – 4. Определитель этой матрицы равен нулю при a = –4.
Ответ: –4.
7. Арифметическое n-мерное векторное пространство