Свойства нормы

1) ||a|| = 0 Û a = о.

2) ||la|| = |l|×||a||, т. к. ||la|| = = = 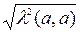|l|×||a||.

3) Неравенство Коши – Буняковского: |(а, b)| £ ||a||×||b||.

Доказательство. Для любого числа λ и любых векторов a, b ≠ 0 выполняется условие (a – lb, a – lb) ³ 0 Þ (a, a) – 2l(a, b) + l²(b, b) ³ 0. Квадратный трехчлен относительно λ неотрицателен при любом λ, если его дискриминант неположителен: D = 4(a, b)² – 4(a, a)(b, b) £ 0 Þ
(a, b)² £ ||a||²×||b||² Þ |(a, b)| £ ||a||×||b||.

4) Неравенство треугольника: ||a + b|| £ ||a|| + ||b||.

Пример 8.11. Будем считать (если нет специальных оговорок), что скалярное произведение равно сумме произведений соответствующих координат.

1. Найти норму вектора а = (, , 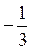). Найдем (a, a):
(a, a) = 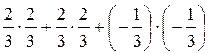= 1 Þ ||a|| = 1.

2. Нормировать вектор b = (–4, 2, 2, –1). Найдем норму вектора ||b||: (b, b) = (–4)² + 2² + 2² + (–1)² = 25 Þ ||b|| = = 5. Вектор e = 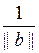×b нормирован, это можно проверить, используя свойство 2, тогда e = 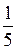×b = (, , , ).

Определение 8.18. Углом между ненулевыми векторами а и b называется угол, меняющийся в пределах от 0 до p и определенный условием .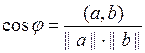

В силу неравенства Коши – Буняковского 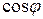принимает значения от (–1) до 1 и, следовательно, угол между ненулевыми векторами определен.

Определение 8.19. Векторы а и b называются ортогональными, если их скалярное произведение равно нулю. Обозначение: а ^ b.

Это определение согласуется с определением угла между векторами.

Определение 8.20. Нулевой вектор считается ортогональным любому вектору.