Связь между координатами вектора и координатами его образа

В пространстве V задан линейный оператор j, а также в некотором базисе e₁, e₂, …, e_n найдена его матрица M(j). Пусть в этом базисе найдены координаты векторов x и j(x): [x] = 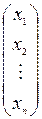, [j(x)] = 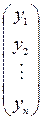. Установим связь между столбцами [x] и [j(x)].

j(х) = y₁e₁ + y₂e₂ + … + y_ne_n;

j(х) = j(x₁e₁ + x₂e₂ + … + x_ne_n) = x₁j(e₁) + x₂j(e₂) + … + x_nj(e_n) =
= x₁(a₁₁e₁ + a₂₁e₂ + … + a_n1e_n) + x₂(a₁₂e₁ + a₂₂e₂ + … + a_n2e_n) + …
… + x_n(a_1ne₁ + a_2ne₂ + … + a_nne_n) = (x₁a₁₁ + x₂a₁₂ + … + x_na_1n)e₁ +
(x₁a₂₁ + x₂a₂₂ + … + x_na_2n)e₂ + … + (x₁a_n1 + x₂a_n2 + … + x_na_nn)e_n.

Вектор j(x) разложен по векторам базиса e₁, e₂, …, e_n двумя способами, но в силу единственности такого разложения коэффициенты при одинаковых базисных векторах можно приравнять:

y₁ = x₁a₁₁ + x₂a₁₂ + … + x_na_1n,

y₂ = x₁a₂₁ + x₂a₂₂ + … + x_na_2n,

…………………………………..

y_n = x₁a_n1 + x₂a_n2 + … + x_na_nn.

Полученные равенства можно записать в матричной форме:

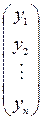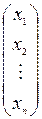= ×или [j(x)] = M(j)×[x].

Теорема 9.2 (о матрице линейного оператора). Если для любого вектора x из пространства V выполняется матричное равенство [j(x)] = В×[x], то матрица B является матрицей линейного оператора j.