Критерий Сильвестра знакоопределенности квадратичной формы

Пусть форма A(x, x) в базисе e = {e₁, e₂, …, e_n} определяется матрицей A(e) = (a_ij),

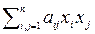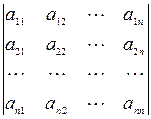A(x, x) = , и пусть D₁ = а₁₁, D₂ = , …, D_n = угловые миноры и определители матрицы (a_ij). Тогда справедливо утверждение:

Теорема 11.4 (критерий Сильвестра).

1. Для того чтобы квадратичная форма A(x, x) была положительно определенной, необходимо и достаточно, чтобы были выполнены неравенства: D₁ > 0, D₂ > 0, …, D_n > 0.

2. Для того чтобы квадратичная форма A(x, x) была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем D₁ < 0.

Пример 11.2. Выяснить, является ли квадратичная форма A(x, x) = 5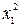 + + 5x₃ + 4x₁x₂ – 8x₁x₃ – 4x₂x₃ положительно определенной?

Решение. Составим матрицу этой квадратичной формы:

M =

Вычислим ее угловые миноры:

D₁ = 5 > 0,

D₂ = = 5 – 4 = 1 > 0,

D₃ = = 25 + 16 + 16 – 16 – 20 – 20 = 1 > 0.

Все угловые миноры положительны, следовательно, квадратичная форма положительно определенна.

Пример 11.3. Выяснить, является ли квадратичная форма A(x, x) = 3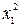 + + 5x₃ + 4x₁x₂ – 8x₁x₃ – 4x₂x₃ положительно определенной?

Решение. Составим матрицу этой квадратичной формы:

M =

Вычислим ее угловые миноры:

D₁ = 3 > 0,

D₂ = 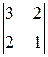= 3 – 4 = –1 < 0,

D₃ = = 15 + 16 + 16 – 16 – 12 – 20 = –1 < 0.

Вывод. Квадратичная форма A(x, x) не является положительно определенной, т. к. D₂ < 0, и отрицательно определенной не является, т. к. D₁ > 0, т.о. она знакопеременная.