рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ЛИНЕЙНАЯ АЛГЕБРА
Реферат Курсовая Конспект
ЛИНЕЙНАЯ АЛГЕБРА
ЛИНЕЙНАЯ АЛГЕБРА - раздел Математика, Федеральное Агентство По Образованию Гоу Впо Кубанский Государственн...
Федеральное агентство по образованию
ГОУ ВПО Кубанский государственный технологический университет
(КубГТУ)
Кафедра прикладной математики
ЛИНЕЙНАЯ АЛГЕБРА
Учебно-методическое пособие по изучению дисциплины и выполнению контрольных работ №1, №2 для студентов-заочников экономической специальности…Введение
Математика за много веков своего существования накопила богатейший набор инструментов для исследования и изучения окружающего мира, научила нас правильно и искусно им пользоваться. К таким инструментам относятся функции и их графики, производная и интеграл, дифференциальные уравнения, их системы, ряды.
Главная роль математики состоит в том, что вместе с решением конкретной задачи она дает общие приемы и способы, применяемые в различных областях практической деятельности инженера.
Реальные процессы связаны с большим количеством переменных, но можно отказаться от каких-то незначительных, частных деталей, акцентируя внимание на некоторых основных сторонах процесса, идеализировав условия протекания этого процесса. Тогда удается построить математическую модель процесса. С помощью основных операций математического анализа можно строить модели достаточно сложных и важных процессов. При этом следует иметь в виду, что разные задачи могут приводить к одной и той же модели, что делает их особо важными для исследовательской деятельности современного инженера.
Инструкция по работе с учебно-методическим пособием
В конце каждой темы приводятся вопросы для самопроверки. В процессе изучения студент должен выполнить контрольную работу, главная цель… В первом семестре Вы должны выполнить одну контрольную работу. Номер варианта соответствует последней цифре шифра…Программа дисциплин
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Матрицы и определители
Пусть дана квадратная матрица второго порядка: Выражение вида называется определителем второго порядка и обозначается:Действия над матрицами.
, , . 2. Произведением матрицы на число называется матрица такая, что , , .Системы линейных уравнений
Правило Крамера решения систем линейных уравнений.Рассмотрим систему: , гдеЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Линейные операции над векторами. Координаты точки. Координаты вектора
Основные теоретические сведения.Вектором называется направленный отрезок прямой или упорядоченная пара точек (про которые известно, какая первая – начало, какая вторая – конец).
Обозначают:  или
или  .
.
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными: 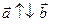 .
.
Действия над векторами
| В геометрической форме: | В координатной форме: | |||
 
| 
| |||
| 1. Сложение | ||||
а) правило параллелограмма
   
 
 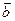 б) правило треугольника
б) правило треугольника
 
 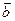
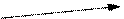

| 
| |||
| 2. Вычитание | ||||
 
 

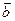
| 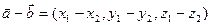
| |||
| 3. Умножение вектора на число | ||||
| 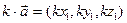 , k- число , k- число
|
Если  , то
, то
1) 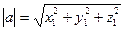 - длина вектора;
- длина вектора;
2) 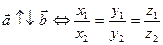 .
.
Если заданы две точки A(x1, y1, z1) , B(x2, y2, z2), то
1) 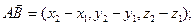
2) если 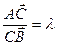 , тогда координаты точки С, делящей отрезок в заданном отношении, находятся по формулам:
, тогда координаты точки С, делящей отрезок в заданном отношении, находятся по формулам:
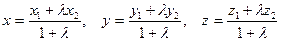
В частности, если С – середина отрезка, то
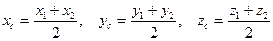 .
.
Скалярное произведение векторов
. Если заданы координаты векторов , то , -Векторное произведение векторов
1) ; 2) ; 3) вектор направлен так, как направлен винт при вращении его по кратчайшему расстоянию от первого перемножаемого…Смешанное произведение векторов
Обозначается: . Если известны координаты векторов , то .Контрольная работа
Перед выполнением контрольной работы необходимо студентам тщательно изучить предложенные темы и разобрать решения приведенных типовых примеров.
Задания на контрольную работу №1
Вариант 1
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
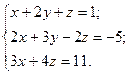
№ 2. Разложить вектор 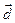 по базису
по базису  ,
, и
и 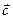 , если
, если 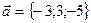 ,
,  ,
, 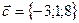 ,
, 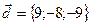 .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 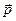 и
и 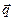 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
 ,
,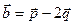 ,
,  ,
,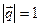 ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
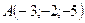 ;
;  ;
; 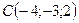 ;
;  .
.
Вариант 2
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
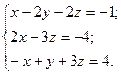
№ 2. Разложить вектор 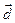 по базису
по базису  ,
, и
и 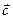 , если
, если 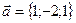 ,
, 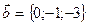 ,
, 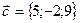 ,
, 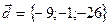 .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 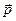 и
и 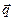 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
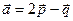 ,
,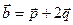 ,
,  ,
, ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
 ;
; 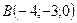 ;
;  ;
;  .
.
Вариант 3
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
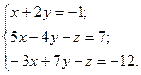
№ 2. Разложить вектор 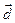 по базису
по базису  ,
, и
и 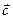 , если
, если 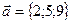 ,
,  ,
, 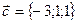 ,
,  .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 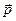 и
и 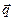 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
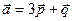 ,
, ,
,  ,
, ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
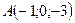 ;
; 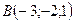 ;
; 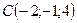 ;
; 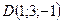 .
.
Вариант 4
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.

№ 2. Разложить вектор 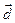 по базису
по базису  ,
, и
и 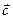 , если
, если 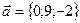 ,
,  ,
, 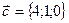 ,
,  .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 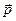 и
и 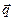 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
 ,
,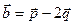 ,
, 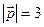 ,
,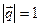 ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
 ;
; 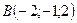 ;
;  ;
;  .
.
Вариант 5
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
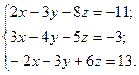
№ 2. Разложить вектор 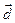 по базису
по базису  ,
, и
и 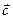 , если
, если 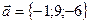 ,
,  ,
,  ,
, 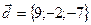 .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 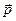 и
и 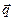 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
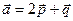 ,
,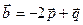 ,
, 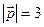 ,
, ,
,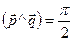 .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
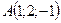 ;
; 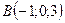 ;
;  ;
; 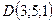 .
.
Вариант 6
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.

№ 2. Разложить вектор 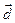 по базису
по базису  ,
, и
и 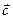 , если
, если 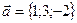 ,
, 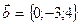 ,
, 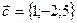 ,
,  .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 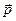 и
и 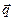 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
 ,
, ,
,  ,
, ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ; 4) длину высоты пирамиды
; 4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
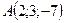 ;
;  ;
; 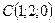 ;
; 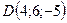 .
.
Вариант 7
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
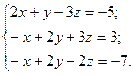
№ 2. Разложить вектор 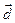 по базису
по базису  ,
, и
и 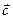 , если
, если  ,
,  ,
,  ,
,  .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 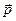 и
и 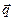 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
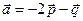 ,
,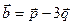 ,
,  ,
, ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
 ;
;  ;
; 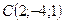 ;
; 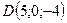 .
.
№ 5. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.

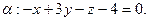
Вариант 8
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
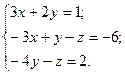
№ 2. Разложить вектор 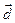 по базису
по базису  ,
, и
и 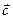 , если
, если 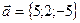 ,
,  ,
,  ,
, 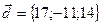 .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 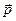 и
и 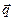 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
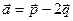 ,
, ,
, 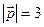 ,
,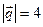 ,
,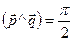 .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
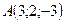 ;
; 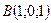 ;
;  ;
; 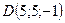 .
.
Вариант 9
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.
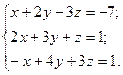
№ 2. Разложить вектор 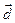 по базису
по базису  ,
, и
и 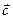 , если
, если  ,
,  ,
,  ,
, 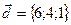 .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 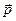 и
и 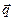 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
 ,
, ,
, 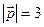 ,
,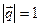 ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
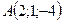 ;
; 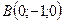 ;
; 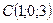 ;
; 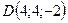 .
.
Вариант 10
№ 1. Дана система трех линейных уравнений с тремя неизвестными. Требуется:
1) найти ее решение с помощью формул Крамера;
2) записать систему в матричной форме и решить ее средствами матричного исчисления; 3) решить методом Гаусса.

№ 2. Разложить вектор 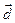 по базису
по базису  ,
, и
и 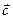 , если
, если  ,
,  ,
,  ,
,  .
.
№ 3. Дано разложение векторов  и
и  по векторам
по векторам 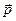 и
и 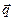 . Требуется найти:
. Требуется найти:
1) длины диагоналей параллелограмма, построенного на векторах  и
и  ;
;
2) косинус угла между векторами  и
и  ;
;
3) площадь параллелограмма, построенного на векторах  и
и  .
.
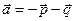 ,
, ,
,  ,
, ,
, .
.
№ 4. По координатам вершин пирамиды  найти:
найти:
1) угол между ребрами  и
и  ;
;
2) площадь треугольника  - основания пирамиды;
- основания пирамиды;
3) объем пирамиды  ;
;
4) длину высоты пирамиды  , опущенную из вершины
, опущенную из вершины ;
;
 ;
;  ;
; 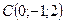 ;
; 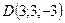 .
.
Задания на контрольную работу № 2
Вариант 1
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
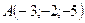 ;
;  ;
; 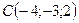 ;
;  .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
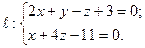

№ 3. Найти точку 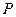 , симметричную точке
, симметричную точке 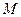 относительно плоскости
относительно плоскости  .
.
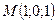 ,
,  .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 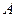 ;
;
2) точку пересечения высоты  и стороны
и стороны 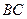 ;
;
3) точку пересечения медиан треугольника  .
.
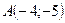 ;
; 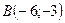 ;
; .
.
№ 5. Составить каноническое уравнение кривой, каждая точка которой равноудалена от точки  и прямой
и прямой  .
.
Вариант 2
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
 ;
; 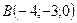 ;
;  ;
;  .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.

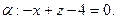
№ 3. Найти точку 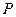 , симметричную точке
, симметричную точке 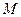 относительно прямой
относительно прямой  .
.
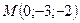 ,
, 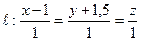 .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 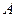 ;
;
2) точку пересечения высоты  и стороны
и стороны 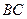 ;
;
3) точку пересечения медиан треугольника  .
.
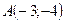 ;
;  ;
; .
.
№ 5. Составить каноническое уравнение кривой, расстояние от каждой точки которой до прямой  в два раза меньше расстояния до точки
в два раза меньше расстояния до точки 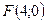 .
.
Вариант 3
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
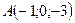 ;
; 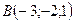 ;
; 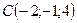 ;
; 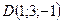 .
.
№ 2 Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
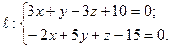

№ 3 Найти точку 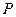 , симметричную точке
, симметричную точке 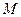 относительно плоскости
относительно плоскости  .
.
 ,
, 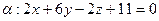 .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 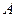 ;
;
2) точку пересечения высоты  и стороны
и стороны 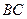 ;
;
3) точку пересечения медиан треугольника  .
.
 ;
; 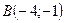 ;
;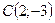 .
.
№ 5. Составить каноническое уравнение кривой, расстояние от каждой точки которой до прямой  в два раза больше расстояния до точки
в два раза больше расстояния до точки 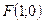 .
.
Вариант 4
№ 1. По координатам вершин пирамиды  найти:
найти:
5) уравнение плоскости  ;
;
6) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
7) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
 ;
; 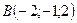 ;
;  ;
;  .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
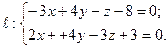

№ 3. Найти точку 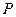 , симметричную точке
, симметричную точке 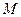 относительно прямой
относительно прямой  .
.
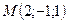 ,
, 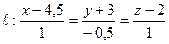 .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 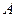 ;
;
2) точку пересечения высоты  и стороны
и стороны 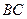 ;
;
3) точку пересечения медиан треугольника  .
.
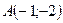 ;
;  ;
;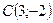 .
.
№ 5. Составить каноническое уравнение кривой, каждая точка которой равноудалена от точки  и прямой
и прямой 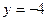 .
.
Вариант 5
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
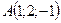 ;
; 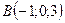 ;
;  ;
; 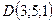 .
.
№ 2 Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
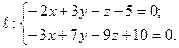
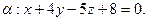
№ 3. Найти точку 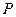 , симметричную точке
, симметричную точке 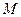 относительно плоскости
относительно плоскости  .
.
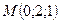 ,
,  .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 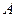 ;
;
2) точку пересечения высоты  и стороны
и стороны 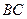 ;
;
3) точку пересечения медиан треугольника  .
.
 ;
; 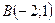 ;
;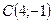 .
.
№ 5. Составить каноническое уравнение кривой, расстояние от каждой точки которой до прямой 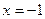 в два раза меньше расстояния до точки
в два раза меньше расстояния до точки  .
.
Вариант 6
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
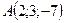 ;
;  ;
; 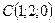 ;
; 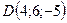 .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.

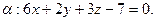
№ 3. Найти точку 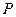 , симметричную точке
, симметричную точке 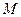 относительно прямой
относительно прямой  .
.
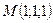 ,
,  .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 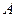 ;
;
2) точку пересечения высоты  и стороны
и стороны 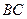 ;
;
3) точку пересечения медиан треугольника  .
.
 ;
; 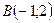 ;
; .
.
№ 5 Составить каноническое уравнение кривой, расстояние от каждой точки которой до прямой 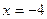 в два раза больше расстояния до точки
в два раза больше расстояния до точки
Вариант 7
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
 ;
;  ;
; 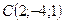 ;
; 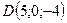 .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.

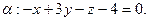
№ 3. Найти точку 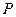 , симметричную точке
, симметричную точке 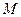 относительно плоскости
относительно плоскости  .
.
 ,
,  .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 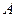 ;
;
2) точку пересечения высоты  и стороны
и стороны 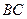 ;
;
3) точку пересечения медиан треугольника  .
.
 ;
;  ;
;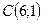 .
.
№ 5. Составить каноническое уравнение кривой, каждая точка которой равноудалена от точки  и прямой
и прямой 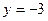 .
.
Вариант 8
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
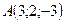 ;
; 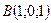 ;
;  ;
; 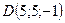 .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.

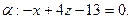
№ 3. Найти точку 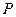 , симметричную точке
, симметричную точке 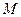 относительно прямой
относительно прямой  .
.
 ,
, 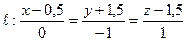 .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 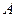 ;
;
2) точку пересечения высоты  и стороны
и стороны 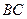 ;
;
3) точку пересечения медиан треугольника  .
.
 ;
;  ;
; .
.
№ 5. Составить каноническое уравнение кривой, расстояние от каждой точки которой до прямой  в два раза меньше расстояния до точки
в два раза меньше расстояния до точки  .
.
Вариант 9
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
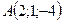 ;
; 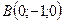 ;
; 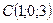 ;
; 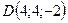 .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.

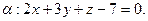
№ 3. Найти точку 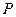 , симметричную точке
, симметричную точке 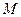 относительно плоскости
относительно плоскости  .
.
 ,
,  .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 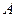 ;
;
2) точку пересечения высоты  и стороны
и стороны 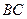 ;
;
3) точку пересечения медиан треугольника  .
.
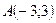 ;
; 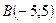 ;
; .
.
№ 5. Составить каноническое уравнение кривой, расстояние от каждой точки которой до прямой 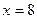 в два раза больше расстояния до точки
в два раза больше расстояния до точки 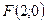 .
.
Вариант 10
№ 1. По координатам вершин пирамиды  найти:
найти:
1) уравнение плоскости  ;
;
2) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
3) угол между ребром  и плоскостью основания
и плоскостью основания  .
.
 ;
;  ;
; 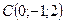 ;
; 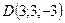 .
.
№ 2. Даны общее уравнение прямой  и плоскость
и плоскость  . Требуется:
. Требуется:
1) составить каноническое уравнение прямой  ;
;
2) найти точку пересечения прямой  с плоскостью
с плоскостью  .
.
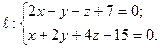
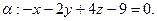
№ 2 Найти точку 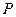 , симметричную точке
, симметричную точке 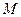 относительно прямой
относительно прямой  .
.
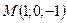 ,
, 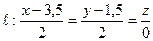 .
.
№ 4. Даны вершины треугольника  . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 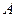 ;
;
2) точку пересечения высоты  и стороны
и стороны 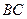 ;
;
3) точку пересечения медиан треугольника  .
.
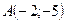 ;
;  ;
; .
.
№ 5. Составить каноническое уравнение кривой, каждая точка которой равноудалена от точки 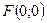 и прямой
и прямой 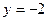 .
.
Содержание и оформление контрольной работы
Контрольную работу следует выполнять в отдельной тетради. Следует указать свой шифр и номер варианта. Условие задачи должно быть полностью переписано перед ее решением.
Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками.
Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.
Вопросы для подготовки к экзамену и зачету
Линейная и векторная алгебра 1. Определители второго, третьего порядка, их свойства. 2. Правило Крамера.Список рекомендуемой литературы
Основная литература
1. Шнейдер В.Е. и др./ Краткий курс высшей математики, / - М.: Высш.шк., 1975 г.
2.Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980 г.
Дополнительная литература
1. Игнатова А.В. и др. Курс высшей математики. М.: Высш.шк., 1964 г.
2. Каплан И.А. Практические занятия по высшей математике.Харьков,1965 г.
Справочная литература (задачники)
1. Клетеник Д.В.Сборник задач по аналитической геометрии.М.:Наука,1975 г.
– Конец работы –
Используемые теги: ная, Алгебра0.05
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ЛИНЕЙНАЯ АЛГЕБРА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?











Новости и инфо для студентов