рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Доверительная вероятность при оценивании генеральной доли (вероятности).
Реферат Курсовая Конспект
Доверительная вероятность при оценивании генеральной доли (вероятности).
Доверительная вероятность при оценивании генеральной доли (вероятности). - раздел Математика, Математическая статистика Пусть Требуется Оценить Неизвестный Генеральный Параметр. Р – Генеральная Дол...
Пусть требуется оценить неизвестный генеральный параметр. Р – генеральная доля (вероятность), т.е. в формуле 17 неизвестным параметром является θ. В качестве оценки Х берем выборочную долю w (в соответствие с теоремой 4). Т.к. по теореме 2 выборочная доля w имеет нормальный закон распределения с параметрами 11, 12, то применим формулу * к случайной величине w:
(19) - доверительная вероятность для оценки доли, где:
- доверительная вероятность для оценки доли, где:
Р – доверительная вероятность;
w – выборочная доля, случайная величина, имеет нормальный закон распределения, оценка;
р – генеральная доля или вероятность признака, неизвестный параметр;
∆ - предельная ошибка;
 - средняя квадратическая ошибка для доли (см. табл. 3, 2-я строчка), среднее квадратическое отклонение для выборочной доли.
- средняя квадратическая ошибка для доли (см. табл. 3, 2-я строчка), среднее квадратическое отклонение для выборочной доли.
Для решения задач:
1. для доли или для средней;
2. определение доверительной вероятности;
3. определение (оценка) предельной ошибки ∆ и доверительного интервала (х-∆; х+∆);
4. определение необходимого объема выборки n – повторная, n' – бесповторная;
Пример:
С целью изучения средней производительности ткачей по схеме случайной бесповторной выборки было отобрано 100 ткачей из 2000. результаты занесены в таблицу.
1) Определить вероятность того, что средняя производительность ткача на всем комбинате отличается от средней производительности в выборке не более чем на 2 метра (по модулю).
Дано:
бесповторная выборка

| производительность в метрах α - β | кол-во ткачей ni | xi | xi *ni | 
|
| 55-65 | 1438,83 | |||
| 65-75 | 2832,2 | |||
| 75-85 | 144,4 | |||
| 85-95 | 1902,69 | |||
| 95-105 | 2620,88 | |||
| m = 5 | n = 100 | 
| 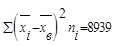
|
Формула доверительной вероятности для средней:

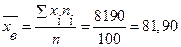 - средняя производительность ткача
- средняя производительность ткача

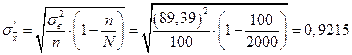
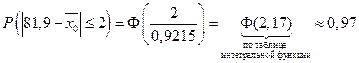
2) В условиях предыдущей задачи определить какова максимальная ошибка Δ и каков доверительный интервал для средней производительности ткача, который можно гарантировать с вероятностью Р = 0,95.
Дано:

Используя формулу 18 и данные, полученные в предыдущей задаче:

 используя таблицу наоборот, получаем
используя таблицу наоборот, получаем 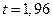



(80,9; 93,71)
Замечание: Доверительный интервал имеет границы, которые являются случайными величинами.
Ответ: с доверительной вероятностью 0,95 можно утверждать, что интервал (80,9; 93,71) генеральную среднюю – среднюю производительность ткачей на всем комбинате.
3) Какой должен быть объем повторной и бесповторной выборок, чтобы в условиях данной задачи с доверительной вероятностью Р равной 0,95 можно было гарантировать ошибку Δ = 1,81 для средней производительности ткачей.
Дано:
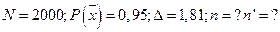
Используя формулу 18 и данные, полученные в предыдущей задаче:

 используя таблицу наоборот, получаем
используя таблицу наоборот, получаем 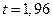
а) пусть выборка повторная:
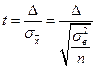
Объем повторной выборки при оценке среднего значения:
(20) 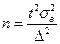
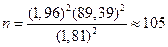
б) бесповторная выборка:
Объем бесповторной выборки при оценке среднего значения:
(21) 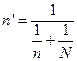

Ответ: нужно обследовать 105 ткачей для повторной выборки (100 для бесповторной) чтобы с вероятностью Р = 0,95 гарантировать наибольшее отклонение Δ = 1,81 для средней производительности ткачей.
4) В условиях исходной задачи определить вероятность того, что доля ткачей, у которых производительность не более 75 метров на всем комбинате отличается от доли таких ткачей в выборке по модулю не более чем на 0,05.
Дано:
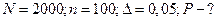
 - выборочная доля
- выборочная доля
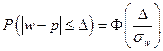
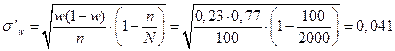
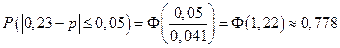
Ответ: с вероятность 0,778 можно утверждать, что доля ткачей, у которых производительность не более 75 метров на всем комбинате отличается от доли таких ткачей в выборке по модулю не более чем на 0,05.
5) В условиях задачи найти Δ и доверительный интервал для доли ткачей на всем комбинате, чья производительность не более 75 метров, который можно гарантировать с вероятностью Р=0,778
Дано:

Используя формулу 19 и данные, полученные в предыдущей задаче:
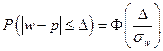
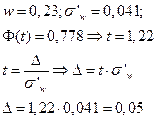
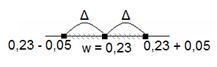
(0,18; 0,28)
Замечание: Доверительный интервал имеет границы, которые являются случайными величинами.
Ответ: с вероятностью 0,778 можно утверждать , что доверительный интервал (0,18; 0,28) содержит генеральную долю ткачей, чья производительность не более 75 метров.
6) В условиях первоначальной задачи определить, сколько надо обследовать ткачей в случае повторной и бесповторной выборки, чтобы с вероятностью Р = 0,778 можно было гарантировать наибольшее отклонение Δ равное 0,05 для доли ткачей, чья производительность не более 75 метров. Ответ дать для случая:
а) когда есть предварительная выборка;
б) когда никаких предварительных данных нет;
Дано:
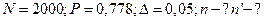
а) предварительная выборка:
1) повторная выборка:

Объем повторной выборки при оценке доли:
(22) 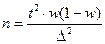

2) бесповторная выборка:

Ответ: нужно обследовать 105 ткачей для повторной выборки (100 для бесповторной) чтобы с вероятностью Р = 0,778 гарантировать Δ = 0,05 для доли ткачей, чья производительность не более 75 метров.
б) никаких предварительных данных нет (т.е. нет исходной таблицы)
Тогда рассмотрим формулу 22 как функцию переменной W:
 и ищем при каких W достигается max этой функции. Можно доказать, что max достигается при w = 0,5. Тогда →
и ищем при каких W достигается max этой функции. Можно доказать, что max достигается при w = 0,5. Тогда →
Объем выборки при оценке доли, если никаких предварительных данных нет:
(23) 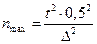

– Конец работы –
Эта тема принадлежит разделу:
Математическая статистика
Вариационный ряд Х размер обуви х Х рост... Таблица... Можно также рассматривать частости для каждой варианты...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Доверительная вероятность при оценивании генеральной доли (вероятности).
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов