рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств
Реферат Курсовая Конспект
Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств
Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств - раздел Математика, Задачи По Математике ...
Задачи по математике
Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств.
Для решения показательно-степенных уравнений и неравенств необходимо знать свойства показательной и степенной функции и уметь ими пользоваться. В этой главе мы рассмотрим данный вопрос.
II.1. Степенная функция и ее свойства.
Прямая пропорциональность. Прямой пропорциональностью называется функция, заданная формулой у = kxn, где число k называется коэффициентом… Перечислим свойства функции у = kx. 1) Область определения функции — множество всех действительных чисел.II. 2. Показательная функция и ее свойства.
Функция, заданная формулой вида у = ах, где а — некоторое положительное число, не равное единице, называется показательной. 1.Функция у = ах при а>1обладает следующими свойствами (см. рис. II.7.): … а) область определения — множество всех действительных чисел;Решение показательно-степенных уравнений, алгоритмы и примеры.
Так называются уравнения вида  , где неизвестное находится и в показателе и в основании степени.
, где неизвестное находится и в показателе и в основании степени.
Можно указать совершенно четкий алгоритм решения уравнении вида  . Для этого надо обратить внимание на то, что при а(х) не равном нулю, единице и минус единице равенство степеней с одинаковыми основаниями (будь-то положительными или отрицательными) возможно лишь при условии равенства показателей То - есть все корни уравнения
. Для этого надо обратить внимание на то, что при а(х) не равном нулю, единице и минус единице равенство степеней с одинаковыми основаниями (будь-то положительными или отрицательными) возможно лишь при условии равенства показателей То - есть все корни уравнения  будут корнями уравнения f(x) = g(x) Обратное же утверждение неверно, при а(х) < 0 и дробных значениях f(x) и g(x) выражения а(х) f(x) и
будут корнями уравнения f(x) = g(x) Обратное же утверждение неверно, при а(х) < 0 и дробных значениях f(x) и g(x) выражения а(х) f(x) и
а(х)g(x) теряют смысл. То - есть при переходе от  к f(x) = g(x) (при
к f(x) = g(x) (при  и
и 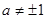 могут появиться посторонние корни, которые нужно исключить проверкой по исходному уравнению. А случаи а = 0, а = 1, а =-1 надо рассмотреть отдельно.
могут появиться посторонние корни, которые нужно исключить проверкой по исходному уравнению. А случаи а = 0, а = 1, а =-1 надо рассмотреть отдельно.
Итак, для полного решения уравнения  рассматриваем случаи:
рассматриваем случаи:
1. а(х) = О . Если при значении х, удовлетворяющем этому уравнению, f(x) и g{x) будут положительными числами, то это решение. В противном случае, нет
2. а(х) = 1. Корни этого уравнения являются корнями и исходного уравнения.
3. а(х) = -1. Если при значении х, удовлетворяющем этому уравнению, f(x) и g(x) являются целыми числами одинаковой четности (либо оба четные, либо оба нечетные) , то это решение. В противном случае, нет
4. При  и
и  решаем уравнение f(x)= g(x) и подстановкой полученных результатов в исходное уравнение отсекаем посторонние корни.
решаем уравнение f(x)= g(x) и подстановкой полученных результатов в исходное уравнение отсекаем посторонние корни.
Примеры решения показательно-степенных уравнений.
Пример №1.

Решение
1) x – 3 = 0, x = 3. т.к. 3 > 0, и 32 > 0, то x1 = 3 - это решение.
2) x – 3 = 1, x2 = 4.
3) x – 3 = -1, x = 2. Оба показателя четные. Это решение x3 = 1.
4) x – 3 ≠ 0 и x ≠ ± 1. x = x2, x = 0 или x = 1. При x = 0, (-3)0 = (-3)0 –верно это решение x4 = 0. При x = 1, (-2)1 = (-2)1 – верно это решение x5 = 1.
Ответ: 0, 1, 2, 3, 4.
Пример №2.

Решение
По определению арифметического квадратного корня: x – 1 ≥ 0, x ≥ 1.
1) x – 1 = 0 или x = 1, 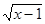 = 0, 00 это не решение.
= 0, 00 это не решение.
2) x – 1 = 1 x 1 = 2.
3) x – 1 = -1 x 2 = 0 не подходит в ОДЗ.
4) 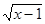 =
= 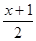




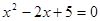
Д = (-2) – 4*1*5 = 4 – 20 = -16 – корней нет.
Ответ: 2.
Пример №3.

Решение
1) 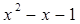 = 0 решения нет, т.к. 0 в любой степени не равен 1.
= 0 решения нет, т.к. 0 в любой степени не равен 1.
2)  ≠ 0 т.е.
≠ 0 т.е.  . Тогда можем записать:
. Тогда можем записать:
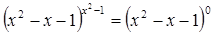
3) 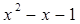 = 1.
= 1.  = 0
= 0
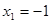 и
и 
4) 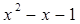 = -1 х = 0 или х = 1. При х = 0
= -1 х = 0 или х = 1. При х = 0 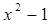 = -1. (-1)-1 ≠ (-1)0. Это не решение. При х = 1 (-1)0 = (-1)0. Это решение х3 = 1.
= -1. (-1)-1 ≠ (-1)0. Это не решение. При х = 1 (-1)0 = (-1)0. Это решение х3 = 1.
5) 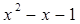 ≠ 0 и
≠ 0 и 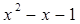 ≠ ±1 имеем
≠ ±1 имеем 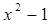 = 0,
= 0,  = -1 или
= -1 или
 = 1. Эти корни уже учтены.
= 1. Эти корни уже учтены.
Ответ: -1, 1, 2.
Пример №4.

Решение
1) При 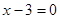 решений нет, т.к. 0 в любой степени не равен 1.
решений нет, т.к. 0 в любой степени не равен 1.
при 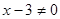 ,
, 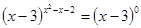
2) 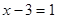 ,
,  .
.
3)  ,
, 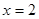 .
.
 , (-1)0 = (-1)0 это решение.
, (-1)0 = (-1)0 это решение.
 .
.
4) 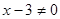 и
и 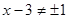

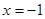 или
или 
При 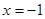 (-4)0 = 1 – верно.
(-4)0 = 1 – верно. 
Ответ: -1, 2, 4.
Пример №5.
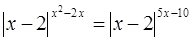
Решение
1) 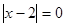 ,
, 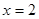 ,
, 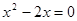 это не решение.
это не решение.
2) 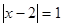 ,
,  и
и  .
.
3) отрицательных значений основание не имеет. При  и
и  ,
, 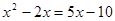 ,
, 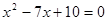 ,
,
х = 5, 315 = 315 – верно. х3 = 5,
х = 2 – не является решением.
Ответ: 1,3,5.
Пример №6
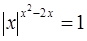
Решение
1)  не дает решений, т.к. 0 ни в какой степени не равен 1.
не дает решений, т.к. 0 ни в какой степени не равен 1.
2)  .
. 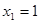 или
или  .
.
3) отрицательных значений 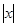 не имеет.
не имеет.
4) При  ,
, 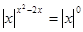
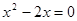 , т.к.
, т.к.  , то
, то 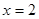 . Проверка 20 = 1 – верно.
. Проверка 20 = 1 – верно. 
Ответ: -1, 1, 2.
Пример №7
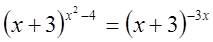
Решение
1)  ,
,  ,
, 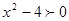 ,
, 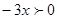 . Это решение
. Это решение  .
.
2) 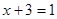 ,
,  .
.
3)  ,
, 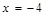 ,
, 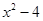 - четное и -3х – четное. Это решение. х2 = -4.
- четное и -3х – четное. Это решение. х2 = -4.
4) 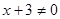 и
и 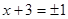 ,
, 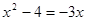 ,
, 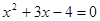 ,
,  , 4-3 = 4-3 – верно.
, 4-3 = 4-3 – верно. 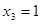 .
.
Ответ: -4, -3, -2, 1
Пример №8

Решение
ОДЗ: 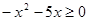 ,
, 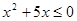
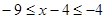 ,
, 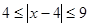 ,
,
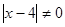 и
и 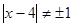

Все решения принадлежат уравнению  =2.
=2.
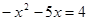 ,
, 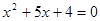 ,
, 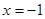 и
и  . Оба значения принадлежат к ОДЗ.
. Оба значения принадлежат к ОДЗ.
Ответ: -4, -1.
Пример №9
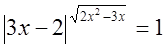
Решение
ОДЗ: 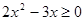 ,
,  ,
, 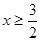 .
.
1) 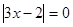 решений не имеет, т.к. 0 в любой степени не равен 1.
решений не имеет, т.к. 0 в любой степени не равен 1.
При 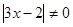 ,
, 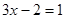 или
или  ,
,
 ОДЗ,
ОДЗ, 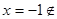 ОДЗ.
ОДЗ.
Значит все решения содержатся в уровнении 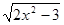 = 0,
= 0,  или
или 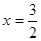 .
.
Проверка:  , 20 = 1 – верно.
, 20 = 1 – верно.
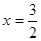 ,
, 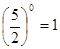 - верно.
- верно.
Ответ: 0, 3/2.
Пример №10
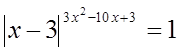
Решение
1)  решений не дает, т.к. 0 в любой степени не равен 1.
решений не дает, т.к. 0 в любой степени не равен 1.
2) При  ,
, 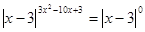 ,
, 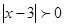 . Все решения принадлежат уравнению
. Все решения принадлежат уравнению  .
.  или
или 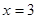 .
.
3) 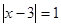 ,
,  и
и  .
.
Второе решение не подходит, т.к 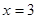 ,
,  . А
. А  является решением
является решением 
Ответ:  , 2, 4.
, 2, 4.
Пример №11

Решение
1) 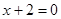 ,
, 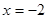 ,
,  и
и  это решение
это решение 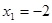 .
.
2) 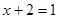 ,
,  .
.
3)  ,
,  ,
,  - четное,
- четное,  - нечетное. Это является решением.
- нечетное. Это является решением.
4)  или
или 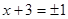 ,
, 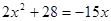 ,
, 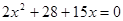 ,
,  ,
,  .
.
Проверка:  ,
,  - верно.
- верно.
Но  не является корнем!
не является корнем!
Выражение (-1,5)52,5, которое получается при проверке не имеет смысла, т.к. степень отрицательно числа имеет смысл только для целых показателей. Равенство  =
=  только для
только для  . Значит, отрицательное число можно возводить только в степень с целым показателем.
. Значит, отрицательное число можно возводить только в степень с целым показателем.
Ответ: -4, -2, -1.
Пример №12

Решение
ОДЗ: 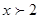 . Значит 0,1 и -1 отпадают.
. Значит 0,1 и -1 отпадают.
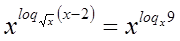 и все решения содержатся в уравнении.
и все решения содержатся в уравнении.
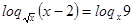
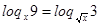 ,
,  ,
, 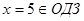
Ответ: 5.
Пример №13

Решение

1)  ,
, 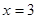 ,
, 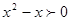 . Это решение
. Это решение  .
.
2) 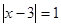 ,
,  ,
,  .
.
3) отрицательных значений  не имеет.
не имеет.
При  или
или  все решения в уравнении
все решения в уравнении 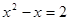 ,
, 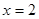 и
и 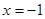 .
.
При 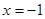 ,
,  - верно.
- верно.  .
.
Ответ: -1, 2, 3, 4.
Пример №14
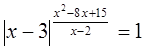
Решение
ОДЗ: 
1) При  решений нет, т.к. 0 в любой степени не равен 1.
решений нет, т.к. 0 в любой степени не равен 1.
При 

2) 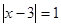 ,
,  и
и 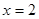 .
.  - решение, а
- решение, а  .
.
3) 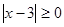 для всех
для всех  . При
. При  и
и 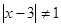 все решения содержатся в уравнении
все решения содержатся в уравнении  ,
, 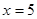 или
или 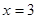 . При
. При 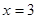 ,
,  .
.
При 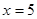 ,
, 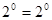 - верно.
- верно. 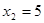 .
.
Ответ: 4, 5.
Пример №15.
 ,
, 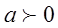
Решение

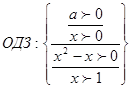
используя свойства логарифма  и
и  получили:
получили:
 =
= 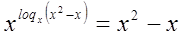
В первой части уравнения выполнили преобразования
 . Получили уравнение
. Получили уравнение 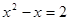 . Все решения содержатся в уравнении.
. Все решения содержатся в уравнении.
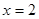 или
или 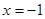 .
. 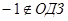
Ответ: 2.
Пример №16
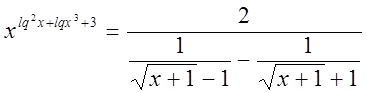
Решение
ОДЗ: 
Преобразуем знаменатель дроби в правой части уравнения
 ;
;  .
.
 ,
,  , где
, где 
1)  ,
,  - верно.
- верно.
2) 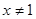 ,
, 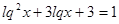
Пасть 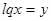 , тогда
, тогда 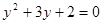

 ,
, 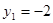 или
или 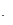
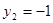 .
.
Следовательно; 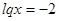 или
или 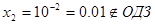 ,
,  ,
,  .
.
Ответ: 1, 0,1, 0, 0,01.
Пример №17
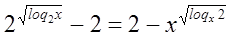
Решение
ОДЗ:  и
и 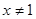
Выполним преобразования.
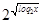 +
+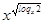 = 2+2
= 2+2
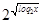 +
+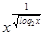 = 4
= 4
Пусть 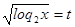 , а
, а 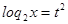 ,
, 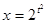
Следовательно, 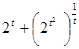 или
или
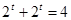 ,
, 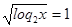
2*2t = 4 
2t = 4/2 
2t = 2
t = 1
Ответ: 2.
Пример №18

Решение
ОДЗ: 
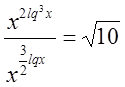 ;
; 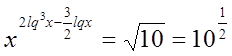
Прологарифмируем обе части равенства:
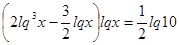
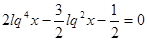 , где
, где 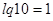 .
.
Умножим обе части уравнения на 2.

Пусть 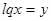 , тогда
, тогда 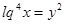
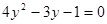

 ,
,  или
или 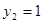
1)  ,
, 
 или
или 

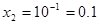
Ответ: 0.1, 10.
Пример №19

Решение
ОДЗ: 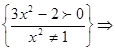
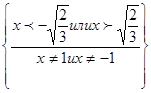
Обратите внимание  ниоткуда не следует! Наоборот, из ОДЗ видно, что
ниоткуда не следует! Наоборот, из ОДЗ видно, что  может быть отрицательным!
может быть отрицательным!
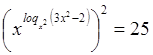
 ,
, 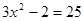
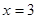 или
или 
Оба значения в ОДЗ.
Так как возводили в квадрат, корни надо проверить.
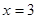 ,
, 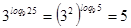 - верно.
- верно.
 ,
,  - верно.
- верно.
Ответ: -3, 3.
Пример №20

ОДЗ: 
Возведем обе части уравнения в квадрат (т.к. они положительны, то посторонние корни не появляются)
 или
или 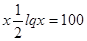
Прологарифмируем по основанию 10.

 или
или 
1)  или
или 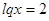
 ,
, 
Ответ: 0.01, 100.
Пример №21

Решение
ОДЗ: 
Прологарифмируем по основанию 10.
 , где
, где 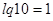 .
.
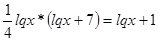
Пусть 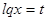 , тогда:
, тогда:
 умножим на 4
умножим на 4

 ,
, 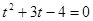
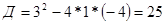
 ,
, 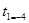 или
или 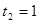
1) 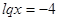

2) 

Ответ: 0,0001, 10.
Пример №22

Решение
ОДЗ: 
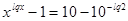
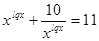
Заменим: 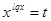 , получим:
, получим:
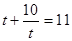 , где
, где  .
.
Решаем уравнение: 
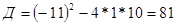
 ;
;  или
или 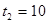
1)  ;
;  ;
;  .
. 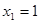 .
.
2) 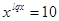 ,
, 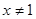 ,
,  ,
,  ,
,  .
.
 ;
;  ;
;  ;
;  .
.
Ответ: 0,1, 1, 10.
Пример №23

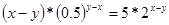
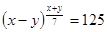
Решение
 и
и 
 :
: 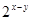

Подставим во второе уравнение вместо 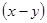 число 5, получим:
число 5, получим:

 или
или 
составляем систему уравнений:





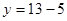

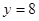

Ответ: (13;8)
Пример №24

Решение
ОДЗ: 

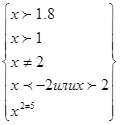

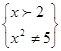
 ;
; 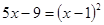
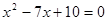 ,
,
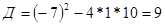
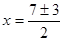 ;
; 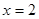 или
или 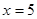
 ,
, 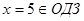 .
.
Ответ: 5.
Пример №25
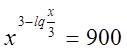
Решение
ОДЗ: 
Прологарифмируем правую и левую части данного уравнения по основанию 10:
Получим:
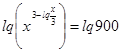 или
или 
Обозначив 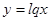 , перепишем записанное уравнение в виде:
, перепишем записанное уравнение в виде:
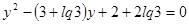 .
.
Решая его относительно  , находим
, находим  ,
, 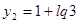 .
.
Используя обозначения 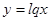 , из первого решения квадратного уравнения имеем
, из первого решения квадратного уравнения имеем 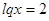 . Отсюда
. Отсюда  . Используя решение
. Используя решение 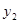 , получаем
, получаем 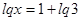 . Преобразуем правую часть этого уравнения:
. Преобразуем правую часть этого уравнения:
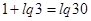 . Значит,
. Значит, 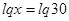 , т.е.
, т.е. 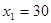 .
.
Ответ: 30, 100.
Пример №26
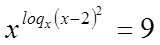
Решение
Так как  , то при
, то при  и
и  имеем равносильное уравнение:
имеем равносильное уравнение:
 или
или 
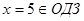 .
.
 ,
, 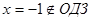
Ответ: 5.
Пример № 27

Решение
ОДЗ: 
Так как обе части уравнения положительны, то прологарифмируем по основанию 10:
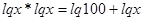

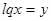 ,
, 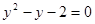

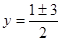 ;
;  или
или 
1)  2)
2) 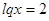
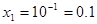

Ответ: 0.1, 100.
Пример №28
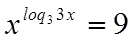
Решение
ОДЗ: 
Так как обе части уравнения положительны, то прологарифмируем по основанию 3:
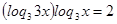

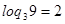 и
и  , поэтому
, поэтому

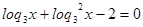

Пусть 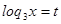 , тогда
, тогда 
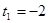 или
или 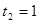 .
.
1) 
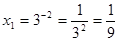 ;
;
2) 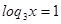

Ответ: 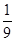 , 3.
, 3.
Пример №29

Решение
1) 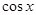
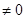 , т.к. 0 в любой степени не равен 1.
, т.к. 0 в любой степени не равен 1.
2)  = 1,
= 1, 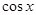 =1,
=1, 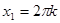 ,
,  или
или
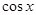 =-1,
=-1,  ,
,  .
.
Так как 1 в любой степени равна 1, то это решения.
3) 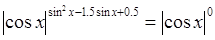 (т.к.
(т.к.  )
)
При 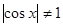 все решения принадлежат уравнению
все решения принадлежат уравнению 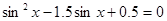 .
.  или
или 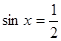 .
.
При 

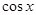 = 0, что не удовлетворяет уравнению
= 0, что не удовлетворяет уравнению 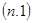

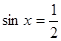 ,
, 
Ответ: 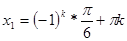 ,
,  .
.
 ,
,  .
.
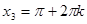 ,
,  .
.
Пример №30

Решение
ОДЗ: 

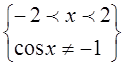
 =
= 
1) 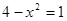 ,
, 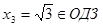 ,
, 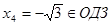 .
.
2) Так как  , то остальные решения получаем из уравнения
, то остальные решения получаем из уравнения  : Отсюда
: Отсюда  или
или  .
. 
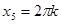 ,
,  и
и 

 ,
,  .
.
Ответ:  , -
, - ,
, 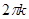 и
и  ,
,  .
.
Пример №31
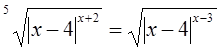
Решение

1)  или
или  ,
,  и
и 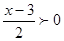 . Это решение.
. Это решение.  .
.
2)  ,
, 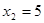 и
и 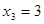
3) Так как 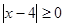 , то
, то  ;
;
 ;
;
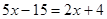
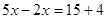
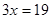
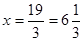 ;
; 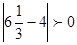 . Это решение.
. Это решение.
Ответ:  ; 5; 3; 4.
; 5; 3; 4.
Пример №32
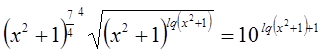
Решение
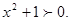 при всех
при всех 

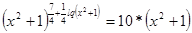
1) 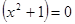 ,
, 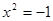 - решений нет.
- решений нет.
2) . Потому при
. Потому при  левая часть равна единице, а правая нет. Это решение.
левая часть равна единице, а правая нет. Это решение.
3) 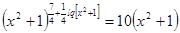 ;
;
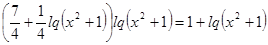 ;
;
 ;
;
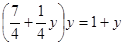 ;
;
 ;
;
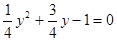 ;
;
 ;
;
 и
и 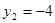 ;
;
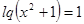 ;
;  ;
;
 ;
; 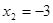 ;
;
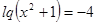 ;
;
 ;
;
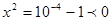 - решений нет.
- решений нет.
Ответ: -3, 3.
Пример №33
Решить графически уравнение:

Решение
У функции 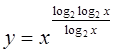 Д(y): x > 0 и log2 x > 0, т.е.,
Д(y): x > 0 и log2 x > 0, т.е.,
x > 1. обл. определения х > 1.
А теперь: 
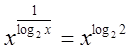 (формула перехода к новому основанию и определение логарифма).
(формула перехода к новому основанию и определение логарифма).
Тогда 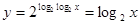 (определение логарифма:
(определение логарифма:  ).
).
Так, что нужно только учитывать, что Д(у): x > 0.
Построим график функции (рис III.1).
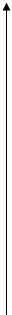
у



 2
2

0 1 4 х
Рис. III.1.
Ответ: (4; 2).
Пример №34
Решить систему уравнений:

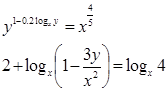
Решение:

По определению логарифма имеем:


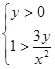

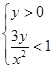





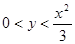 .
.
Прологарифмируем первое уравнение системы по основанию х.
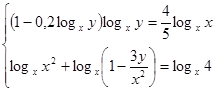



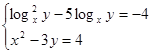 .
.
Из второго уравнения системы выразим у через х:
 ,
, 
Тогда: 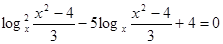
Пусть  ,
,  , Д = (-5)2 -4*1*4 = 9,
, Д = (-5)2 -4*1*4 = 9,  ,
,  или
или  .
.
1)  2)
2) 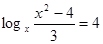
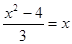


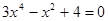
Д = (-3)2 – 4*1*(-4) = 25 пусть 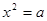 , тогда
, тогда


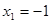 или
или  Д = (-1)2 – 4*3*4 = -47<0
Д = (-1)2 – 4*3*4 = -47<0
 или
или  корней нет
корней нет
(-1,-1) – удовлетворяет ОДЗ
(4,4) решение системы уравнений.
Ответ: (4, 4).
Пример №35
Решите систему уравнений:
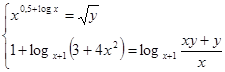
Решение.

По определению логарифма имеем:
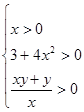



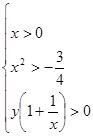
Основание логарифма может быть:
1)  (дробное)
(дробное)
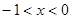
(-1, 0) – не удовлетворяет ОДЗ.
2) 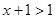
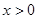
Выполним преобразования:
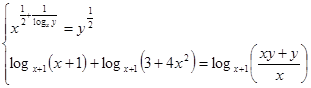
Прологарифмируем первое уравнение системы по основанию х:
 ,
,
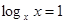 ,
,  ,
,
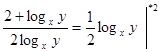
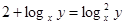 или
или 
Пусть 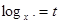 , тогда
, тогда 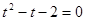
Д = (-)2 -4*1*(-2) = 9
 или
или 
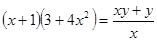

 : (х+1)
: (х+1)

 , где
, где 
 ;
;
1) 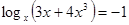
 или
или 

Решаем биквадратное уравнение
Примем 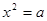 , тогда получим
, тогда получим 
D = 32 – 4*1*(-4) = 25
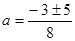 ;
; 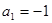 или
или 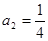
а) 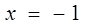
б)  ;
; 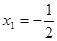 (не удовлетворяет ОДЗ)
(не удовлетворяет ОДЗ)
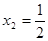

 - решение системы уравнений.
- решение системы уравнений.
2) 
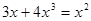


 или
или 
 - (не удовлетворяет ОДЗ)
- (не удовлетворяет ОДЗ)
D = (-1)2 -4*4*3 = -47 – корней нет.
Ответ:  . [ ]
. [ ]
Пример № 36

Решение
Для любого х 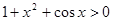 и
и  ОДЗ этого уравнения состоит из всех х удовлетворяющих условию
ОДЗ этого уравнения состоит из всех х удовлетворяющих условию 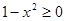 , т.е. ОДЗ есть множество всех х из промежутка
, т.е. ОДЗ есть множество всех х из промежутка 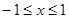 на этом множестве. Исходное уравнение равносильно совокупности уравнений.
на этом множестве. Исходное уравнение равносильно совокупности уравнений.
 и
и 
Решаем ее.





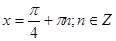
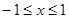 принадлежат
принадлежат 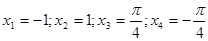 . Они и являются решениями исходного уравнения.
. Они и являются решениями исходного уравнения.
Ответ:  .
.
Глава IV. Решение показательно-степенных неравенств, план решения и примеры.
Неравенства вида  (или меньше) при а(х)>0 и
(или меньше) при а(х)>0 и 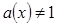 решаются на основании свойств показательной функции: для 0 < а(х) < 1 при сравнении f(x) и g(x) знак неравенства меняется, а при а(х) > 1 – сохраняется.
решаются на основании свойств показательной функции: для 0 < а(х) < 1 при сравнении f(x) и g(x) знак неравенства меняется, а при а(х) > 1 – сохраняется.
Самый сложный случай при а(х) < 0. Здесь можно дать только общее указание: определить, при каких значениях х показатели f(x) и g(x) будут целыми числами, и выбрать из них те, которые удовлетворяют условию
Наконец, если исходное неравенство будет выполняться при а(х) = 0 или а(х) = 1 (например, когда неравенства нестрогие), то нужно рассмотреть и эти случаи.
Пример 1.
Решить неравенство:
23x:+7 < 22x-1.
Решение.
Здесь основание степени больше 1, поэтому, сравнивая показатели, запишем неравенство того же смысла: Зх + 7 < 2х - 1. Решив это неравенство, получим х < - 8.
Ответ: -8.
Пример 2.
Решить неравенство:

Решение.
Так как 625 = 252= 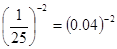 , то заданное неравенство можно записать в виде
, то заданное неравенство можно записать в виде 
Так как 0 < 0,04 < 1, то, сравнивая показатели, запишем неравенство противоположного смысла 5х - х2 - 8 = -2. Имеем последовательно
 ,
,
 ,
,
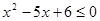 ,
,
 .
.
Решив последнее неравенство, получим 2  х
х  3.
3.
Таким образом множество решений заданного неравенства есть отрезок [2; 3].
Ответ: [2; 3].
Пример 3.
Решим неравенство
Зх < 4.
Решение
Пользуясь тем, что 0,5 -2 = 4, перепишем заданное неравенство в виде
0,57-Зх < 0,5-2. Показательная функция y= 0,5x убывает (основание 0,5 меньше 1). Поэтому данное неравенство равносильно неравенству 7 – Зх > - 2, откуда х < 3.
Ответ: ( — оо ; 3).
Пример 4.
Решим неравенство
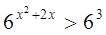
Показательная функция y = 6x возрастает. Поэтому данное неравенство равносильно неравенству х2 + 2x > 3, решая которое, получим: (-оо; -3)
и (1; оо).
Ответ: (-оо; -3) и (1; оо).
Пример 5.
Решим неравенство:

Сделаем замену  , тогда
, тогда 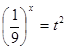 и неравенство перепишется в виде
и неравенство перепишется в виде  , откуда
, откуда  . Следовательно, решением данного неравенства являются числа х, удовлетворяющие неравенствам
. Следовательно, решением данного неравенства являются числа х, удовлетворяющие неравенствам 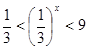 , и только такие числа. Но
, и только такие числа. Но 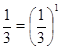 ,
,  , а функция
, а функция 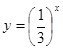 убывает,
убывает,
поскольку  < 1. Поэтому решением неравенств
< 1. Поэтому решением неравенств 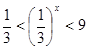 будут числа х, удовлетворяющие неравенствам - 2 < х < 1.
будут числа х, удовлетворяющие неравенствам - 2 < х < 1.
Ответ: ( - 2; 1).
Пример 6.
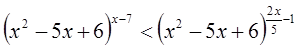
Решение
1) 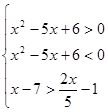
















 2 3
2 3 
 10
10
Изобразим на числовом луче
Должны выполняться все три неравенства, т.к. это система. Но при  взятое не выполняется. Решений нет.
взятое не выполняется. Решений нет.
2) 

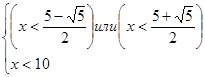
 Изобразим на числовом луче
Изобразим на числовом луче






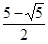
 10
10
Если  , то
, то 
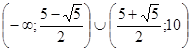 -решение системы неравенств.
-решение системы неравенств.
Остальные случаи не дают решений, т.к. 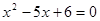 или 1 не удовлетворяют условию, а при
или 1 не удовлетворяют условию, а при  т.е.
т.е.  получаем отрицательные числа с дробными показателями степени.
получаем отрицательные числа с дробными показателями степени.
Ответ: 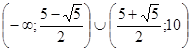
Пример 7

Решение
При 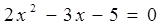 , х = 2,5 или х = -1
, х = 2,5 или х = -1
При  или
или  можно записать
можно записать 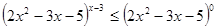 .
.


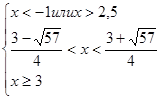
При  второе неравенство не выполняется. Система решений не имеет.
второе неравенство не выполняется. Система решений не имеет.
Изобразим на числовом луче решение системы неравенств










 -1 2,5
-1 2,5  3
3
Система не имеет решений.
2)


Изобразим на числовом луче решение системы неравенств







 решение системы неравенств.
решение системы неравенств.
3)  ,
,  - выражение
- выражение  имеет смысл тогда, когда х – 3 – целое число, чтобы показатель х – 3 был целым числом. Таким образом х – целое число в промежутке (-1; 2,5) т.е. х может принимать значения 0,1,2.
имеет смысл тогда, когда х – 3 – целое число, чтобы показатель х – 3 был целым числом. Таким образом х – целое число в промежутке (-1; 2,5) т.е. х может принимать значения 0,1,2.
Проверка:
При  - верно.
- верно.
При 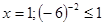 - верно.
- верно.
При  - верно.
- верно.
4) 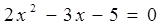 , х2 = 2,5 и х1 = -1
, х2 = 2,5 и х1 = -1
При х = -1 – не имеет смысла выражение 0-4.
При х = 2,5, 02,5 – не имеет смысла.
5) 
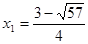 ;
; 
При  ;
; 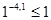 - верно.
- верно.
При 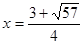 ;
; 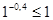 - верно.
- верно.
Ответ: 
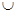
 или
или 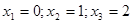 .
.
Задачи и решения.
1. Ответ: . 2. Ответ: 2. 3. Ответ: 7; 14.– Конец работы –
Используемые теги: Функции, Свойства, используемые, решении, показательно-степенных, уравнений, неравенств0.092
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов