Теоретические кривые распределения
Из определенного числа теоретических кривых распределения, используемых наиболее часто для моделирования и выравнивания эмпирических рядов распределения, рассмотрим только кривую нормального распределения и кривую распределения Пуассона и их применение в статистических исследованиях.
Кривая нормального распределения. Данный тип теоретических кривых распределения наиболее часто используется в экономических исследованиях, поскольку многие теоретические кривые в пределе сходятся к нормальному распределению.
С помощью кривой нормального распределения описываются только непрерывные случайные величины. Однако любой дискретный экономический процесс, с определенными допущениями, может быть рассмотрен как процесс непрерывной случайной величины. Наиболее наглядной и информативной формой выражения нормального распределения является функция плотности распределения вероятности
 (6.1)
(6.1)
где xi – i-е значение (варианта) изучаемого признака (случайная величина);
 – математическое ожидание (среднее значение);
– математическое ожидание (среднее значение);
σ – стандартное отклонение.
Функция плотности распределения вероятности еще называется нормальной кривой и графически может быть выражена следующим образом (рис. 6.2.). Числовыми характеристиками нормальной кривой являются ее параметры ( , σ), которые определяют положение и форму нормальной кривой на графике.
, σ), которые определяют положение и форму нормальной кривой на графике.
 Параметр
Параметр  определяет только положение кривой на графике. При его изменении нормальная кривая перемещается вдоль оси абсцисс, а форма кривой при этом не изменяется. Параметр σ определяет только форму нормальной кривой, т.е. его изменение приводит к изменению формы кривой. На рис.6.3. показаны две формы кривой. У кривой 1 стандартное отклонение (σ1) меньше, чем у кривой 2 (σ2), т.е. σ1<σ2. Кривая нормального распределения обладает определенными свойствами. Отметим только основные.
определяет только положение кривой на графике. При его изменении нормальная кривая перемещается вдоль оси абсцисс, а форма кривой при этом не изменяется. Параметр σ определяет только форму нормальной кривой, т.е. его изменение приводит к изменению формы кривой. На рис.6.3. показаны две формы кривой. У кривой 1 стандартное отклонение (σ1) меньше, чем у кривой 2 (σ2), т.е. σ1<σ2. Кривая нормального распределения обладает определенными свойствами. Отметим только основные.
 1.Относительно среднего значения
1.Относительно среднего значения  нормальная кривая симметрична. Это означает, что плотность распределения вероятности на одном и том же расстоянии слева и справа от
нормальная кривая симметрична. Это означает, что плотность распределения вероятности на одном и том же расстоянии слева и справа от  имеет одинаковое значение. Если дискретная случайная величина (которая графически выражается в виде полигона) соответствует нормальному распределению, то она также будет симметрична относительно
имеет одинаковое значение. Если дискретная случайная величина (которая графически выражается в виде полигона) соответствует нормальному распределению, то она также будет симметрична относительно  . А это значит, что частоты (или частости) на одном и том же расстоянии слева и справа от
. А это значит, что частоты (или частости) на одном и том же расстоянии слева и справа от  имеет одинаковое значение.
имеет одинаковое значение.
2.Поскольку нормальная кривая является симметричной, постольку среднее значение  равно моде
равно моде 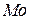 и медиане
и медиане  , т.е.
, т.е.  . А это означает, что для непрерывной случайной величины в точке
. А это означает, что для непрерывной случайной величины в точке  нормальная кривая имеет наибольшую плотность и вся совокупность случайных величин разделена пополам. Кроме того, с учетом симметричности, коэффициенты асимметрии
нормальная кривая имеет наибольшую плотность и вся совокупность случайных величин разделена пополам. Кроме того, с учетом симметричности, коэффициенты асимметрии  и эксцесса
и эксцесса 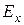 равны нулю.
равны нулю.
3.На расстоянии  от значения
от значения  , т.е.
, т.е.  , нормальная кривая имеет точки перегиба. Относительно этих точек происходит неравномерное изменение абсолютного прироста плотности случайной величины. Так, например, при изменении непрерывной случайной величины от –∞ до точки перегиба (
, нормальная кривая имеет точки перегиба. Относительно этих точек происходит неравномерное изменение абсолютного прироста плотности случайной величины. Так, например, при изменении непрерывной случайной величины от –∞ до точки перегиба ( абсолютный прирост плотности случайной величины возрастает от бесконечно малого до максимального значения. А при изменении случайной величины от точки перегиба (
абсолютный прирост плотности случайной величины возрастает от бесконечно малого до максимального значения. А при изменении случайной величины от точки перегиба ( до
до  абсолютный прирост плотности непрерывной случайной величины изменяется от максимального значения до нуля. От
абсолютный прирост плотности непрерывной случайной величины изменяется от максимального значения до нуля. От  до +∞ абсолютный прирост плотности случайной величины изменяется в обратном порядке.
до +∞ абсолютный прирост плотности случайной величины изменяется в обратном порядке.
График дискретной случайной величины в виде полигона не имеет точки перегиба, но характер изменения абсолютного прироста дискретной случайной величины в качественном плане близок к характеру изменения абсолютного прироста плотности непрерывной случайной величины.
4.На отрезке [(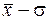 ), (
), ( )] оси абсцисс расположено 68,3% всех значений непрерывной случайной величины. А на отрезке [(
)] оси абсцисс расположено 68,3% всех значений непрерывной случайной величины. А на отрезке [( ), (
), ( +2σ)] оси абсцисс расположено 95,4% всех значений непрерывной случайной величины. Эти цифры характеризуют степень концентрации случайной величины вокруг ее среднего значения при ее нормальном распределении. Для дискретной случайной величины отмеченные оценки распределения непрерывной случайной величины в указанной точности не выполняются и имеют приблизительное значение. Однако, чем больше будет использовано число наблюдений дискретной случайной величины и чем меньше будут размеры интервалов групп признака, тем ближе будут оценки распределения дискретной случайной величины к отмеченным оценкам непрерывной случайной величины. Это свойство позволяет понять, как при нормальном распределении расположены фактические значения изучаемого экономического процесса.
+2σ)] оси абсцисс расположено 95,4% всех значений непрерывной случайной величины. Эти цифры характеризуют степень концентрации случайной величины вокруг ее среднего значения при ее нормальном распределении. Для дискретной случайной величины отмеченные оценки распределения непрерывной случайной величины в указанной точности не выполняются и имеют приблизительное значение. Однако, чем больше будет использовано число наблюдений дискретной случайной величины и чем меньше будут размеры интервалов групп признака, тем ближе будут оценки распределения дискретной случайной величины к отмеченным оценкам непрерывной случайной величины. Это свойство позволяет понять, как при нормальном распределении расположены фактические значения изучаемого экономического процесса.
Для проведения практических расчетов формула функции плотности распределения вероятности (6.1) малопригодна. Поэтому случайную величину 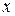 , имеющую конкретную единицу измерения, заменяют стандартной случайной величиной
, имеющую конкретную единицу измерения, заменяют стандартной случайной величиной  , которая является безразмерной и называется нормированной. В отдельных литературных источниках она обозначается буквой
, которая является безразмерной и называется нормированной. В отдельных литературных источниках она обозначается буквой  . Для замены исходной случайной величины на нормированную используется следующее выражение:
. Для замены исходной случайной величины на нормированную используется следующее выражение:
 . (6.2)
. (6.2)
В результате замены мы получаем функцию плотности стандартной нормальной величины  . (6.3)
. (6.3)
Параметры полученной функции величины имеют постоянные значения. Так, математическое ожидание новой случайной величины  равно нулю, т.е.
равно нулю, т.е.  , а дисперсия – единице, т.е.
, а дисперсия – единице, т.е.  . Это позволят определить значения функции плотности распределения вероятности в стандартизированной форме для различных значений случайной величины
. Это позволят определить значения функции плотности распределения вероятности в стандартизированной форме для различных значений случайной величины  . Значения функции плотности распределения вероятности табулированы и приведены в приложении 1, которая имеет следующий вид (табл. 6.2)
. Значения функции плотности распределения вероятности табулированы и приведены в приложении 1, которая имеет следующий вид (табл. 6.2)
Таблица 6.2
| u | ||||||||||
| 0,0 0,1 0,2 и т.д. | 0,3989 |
В табл.6.2 все значения 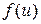 представлены в десятичной форме и все они меньше единицы (хотя ноль целых нигде не показан, за исключением первого значения). В первом столбце переменная
представлены в десятичной форме и все они меньше единицы (хотя ноль целых нигде не показан, за исключением первого значения). В первом столбце переменная  имеет значения с одним знаком после запятой. Второй знак после запятой приведен в первой строке таблицы. Например, чтобы найти значение плотности нормального распределения в стандартизированной форме
имеет значения с одним знаком после запятой. Второй знак после запятой приведен в первой строке таблицы. Например, чтобы найти значение плотности нормального распределения в стандартизированной форме 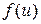 для
для  , вначале выбирают строку с
, вначале выбирают строку с  , затем выбирают столбец с цифрой 5. Пересечение выбранной строки и столбца дает искомое значение функции. Так, для рассматриваемого примера
, затем выбирают столбец с цифрой 5. Пересечение выбранной строки и столбца дает искомое значение функции. Так, для рассматриваемого примера 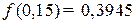 .
.
Кривая распределения Пуассона. Данный тип теоретических кривых распределения используется в тех исследованиях, где варианты признака  носят дискретный характер, а вероятность наступления события с ростом значения признака падает. Кривую распределения Пуассона еще называют распределением редких событий. Типичным примером проявления закона Пуассона является вероятность дожития человека до определенных лет. Чем большее число лет (60, 70, 80 и т.д.), которое может прожить человек (оно задается нами), тем меньше будет вероятность, что человек доживет до этих лет.
носят дискретный характер, а вероятность наступления события с ростом значения признака падает. Кривую распределения Пуассона еще называют распределением редких событий. Типичным примером проявления закона Пуассона является вероятность дожития человека до определенных лет. Чем большее число лет (60, 70, 80 и т.д.), которое может прожить человек (оно задается нами), тем меньше будет вероятность, что человек доживет до этих лет.
Использование распределения Пуассона предполагает, что совокупность единиц наблюдения достаточно велика ( ), а средняя арифметическая и дисперсия эмпирического ряда либо равны, либо незначительно отличаются друг от друга.
), а средняя арифметическая и дисперсия эмпирического ряда либо равны, либо незначительно отличаются друг от друга.
Кривую распределения Пуассона используют при исследовании качества продукции (например, оценка числа обрывов нитей при ткачестве), в теории надежности (например, описание числа отказов в работе оборудования в единицу времени), в теории массового обслуживания (например, описание поступления числа заявок на обслуживание в ремонтных мастерских, торговых точках в единицу времени).
Кривая распределения Пуассона описывается следующей функцией:
 , (6.4)
, (6.4)
где λ – параметр распределения Пуассона; λ=np ;
m– случайная величина.