Теория множеств
Теория множеств
Вариант 1.
1. Известно, что из 60 туристов знают немецкий язык – 15, французский – 20, английский – 25, немецкий и французский – 5, немецкий и английский – 5, французский и английский – 10, все три иностранные языки – 3. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что 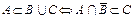 .
.
4. Даны множества 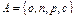 и
и  . Найти
. Найти  ,
,  ,
, 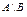 ,
, 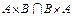 ,
, 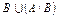 .
.
5. Доказать, что для всех натуральных чисел выполняется утверждение:
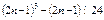 .
.
6. Пусть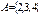 ,
, 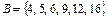 . Опишите с помощью графа или таблицы отношение
. Опишите с помощью графа или таблицы отношение  ,
,  ,
,  .
.
7. Верно ли высказывание: Если отношения R и S рефлексивны, то отношение R S рефлексивно.
S рефлексивно.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что конечное множество не может быть равномощным своему подмножеству.
Вариант 2.
1. Известно, что из 50 туристов знают немецкий язык – 20, французский – 35, английский – 25, немецкий и французский – 10, немецкий и английский – 5, французский и английский – 7, все три иностранные языки – 2. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество: 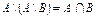 .
.
3. Доказать, что:  .
.
4. Даны множества 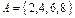 и
и  . Найти
. Найти  ,
,  ,
, 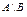 ,
, 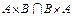 ,
, 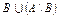 .
.
5. Доказать, что для всех 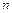 выполняется утверждение:
выполняется утверждение:
 .
.
6. Пусть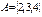 ,
, 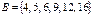 . Опишите с помощью графа или таблицы отношение
. Опишите с помощью графа или таблицы отношение  ;
;  .
.
7. Верно ли высказывание: Если отношения R и S рефлексивны, то отношение R 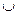 S рефлексивно.
S рефлексивно.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Показать, что если А и В бесконечны и А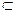 В, то А и В могут быть равномощными в смысле возможности взаимнооднозначного соответствия элементов множеств.
В, то А и В могут быть равномощными в смысле возможности взаимнооднозначного соответствия элементов множеств.
Вариант 3.
1. Известно, что из 80 туристов знают немецкий язык – 20, французский – 25, английский – 35, немецкий и французский – 5, немецкий и английский – 10, французский и английский – 7, все три иностранные языки – 2. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество: 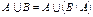 .
.
3. Доказать, что:  .
.
4. Даны множества  и
и  . Найти
. Найти 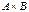 ,
,  ,
, 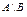 ,
,  ,
, 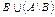 .
.
5. Доказать, что для всех 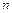 выполняется утверждение:
выполняется утверждение:
 .
.
6. Пусть 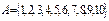 . Опишите отношение
. Опишите отношение  ,
, 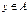 ,
,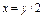 с помощью графа или таблицы.
с помощью графа или таблицы.
7. Верно ли высказывание: Если отношения R и S рефлексивны, то отношение RS рефлексивно.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что множества точек произвольных многоугольников на плоскости равномощны.
Вариант 4.
1. Известно, что из 50 туристов знают немецкий язык – 10, французский – 20, английский – 20, немецкий и французский – 6, немецкий и английский – 6, французский и английский – 5, все три иностранные языки – 3. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что:  .
.
4. Даны множества  и
и 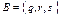 . Найти
. Найти 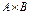 ,
, 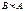 ,
,  ,
,  ,
,  .
.
5. Доказать, что для всех 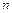 выполняется утверждение:
выполняется утверждение:
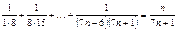 .
.
6. Пусть 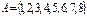 . Опишите отношение
. Опишите отношение  ,
, 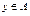 ,
,  . Найдите и опишите с помощью графа или таблицы отношение «не R».
. Найдите и опишите с помощью графа или таблицы отношение «не R».
7. Верно ли высказывание: Если отношения R и S симметричны, то отношение R S симметрично.
S симметрично.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что каждое бесконечное подмножество счетного множества является счетным.
Вариант 5.
1. Известно, что из 90 туристов знают немецкий язык – 40, французский – 30, английский – 20, немецкий и французский – 8, немецкий и английский – 5, французский и английский – 10, все три иностранные языки – 3. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество: 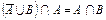 .
.
3. Доказать, что: 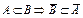 .
.
4. Даны множества  и
и  . Найти
. Найти  ,
,  ,
,  ,
, 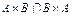 ,
, 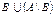 .
.
5. Доказать, что для всех 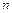 выполняется утверждение:
выполняется утверждение:
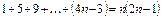 .
.
6. Заданы множества 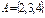 ,
,  . Опишите с помощью графа или таблицы отношение
. Опишите с помощью графа или таблицы отношение 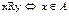 ,
,  ,
,  . Найдите и опишите с помощью графа или таблицы отношение «не R».
. Найдите и опишите с помощью графа или таблицы отношение «не R».
7. Верно ли высказывание: Если отношения R и S симметричны, то отношение R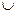 S симметрично.
S симметрично.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что если А бесконечное множество, а В конечное или счетное, то |А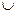 В| = |A|.
В| = |A|.
Вариант 6.
1. Известно, что из 95 туристов знают немецкий язык – 25, французский – 30, английский – 40, немецкий и французский – 5, немецкий и английский – 10, французский и английский – 8, все три иностранные языки – 3. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что: 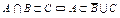 .
.
4. Даны множества 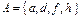 и
и  . Найти
. Найти 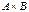 ,
, 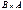 ,
,  ,
,  ,
, 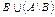 .
.
5. Доказать, что для всех 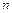 выполняется утверждение:
выполняется утверждение:
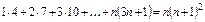 .
.
6. Заданы множество 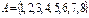 . Опишите отношение
. Опишите отношение 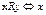 ,
, 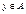 ,
,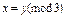 . Построить матрицу отношения R -1.
. Построить матрицу отношения R -1.
7. Верно ли высказывание: Если отношения R и S антисимметричны, то отношение R S антисимметрично.
S антисимметрично.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что если А бесконечное множество и несчетное, а В конечное или счетное, то |АВ| = |A|.
Вариант 7.
1. Известно, что из 80 туристов знают немецкий язык – 20, французский – 35, английский – 25, немецкий и французский – 10, немецкий и английский – 5, французский и английский – 7, все три иностранные языки – 2. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что: 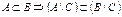 .
.
4. Даны множества 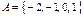 и
и  . Найти
. Найти  ,
,  ,
, 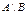 ,
, 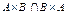 ,
, 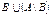 .
.
5. Доказать, что для всех 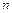 выполняется утверждение:
выполняется утверждение:
 .
.
6. Заданы множество 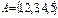 и отношение
и отношение , где
, где .
.
7. Верно ли высказывание: Если отношения R и S антисимметричны, то отношение R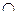 S антисимметрично.
S антисимметрично.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что множества точек квадрата и отрезка равномощны.
Вариант 8.
1. Известно, что из 60 туристов знают немецкий язык – 15, французский – 20, английский – 25, немецкий и французский – 5, немецкий и английский – 5, французский и английский – 10, все три иностранные языки – 3. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что: 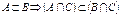 .
.
4. Даны множества  и
и 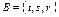 . Найти
. Найти  ,
, 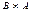 ,
, 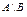 ,
,  ,
, 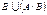 .
.
5. Доказать, что для всех 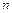 выполняется утверждение:
выполняется утверждение:
 .
.
6. Заданы множество  и отношение
и отношение  ,
, 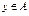 ,
,  . Построить матрицу отношения «не R».
. Построить матрицу отношения «не R».
7. Верно ли высказывание: Если отношения R и S транзитивны, то отношение R S транзитивно.
S транзитивно.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что для каждого бесконечного множества А существует собственное подмножество В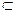 А, для которого |A| = |B|.
А, для которого |A| = |B|.
Вариант 9.
1. Известно, что из 85 туристов знают немецкий язык – 20, французский – 30, английский – 35, немецкий и французский – 10, немецкий и английский – 5, французский и английский – 7, все три иностранные языки – 2. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что:  .
.
4. Даны множества 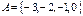 и
и  . Найти
. Найти  ,
,  ,
, 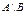 ,
, 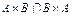 ,
, 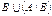 .
.
5. Доказать, что для всех 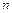 выполняется утверждение:
выполняется утверждение:
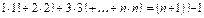 .
.
6. Заданы множество  и отношение
и отношение 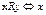 ,
, 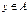 ,
,  . Построить матрицу отношения R -1.
. Построить матрицу отношения R -1.
7. Верно ли высказывание: Если отношения R и S транзитивны, то отношение R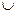 S транзитивно.
S транзитивно.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что если А – счетное множество, В – конечное множество, то АВ – счетное множество.
Вариант 10.
1. Известно, что из 65 туристов знают немецкий язык – 17, французский – 23, английский – 25, немецкий и французский – 7, немецкий и английский – 8, французский и английский – 6, все три иностранные языки – 4. Сколько туристов знают только один из иностранных языков? Сколько не знают ни одного?
2. Доказать тождество:  .
.
3. Доказать, что:  .
.
4. Даны множества 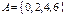 и
и  . Найти
. Найти  ,
,  ,
, 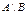 ,
, 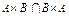 ,
, 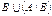 .
.
5. Доказать, что для всех 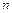 выполняется утверждение:
выполняется утверждение:
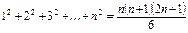 .
.
6. Заданы множество  и отношение
и отношение  ,
, 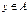 ;
;  . Построить матрицу отношения «не R».
. Построить матрицу отношения «не R».
7. Верно ли высказывание: Если отношения R и S антисимметричны, то отношение R S антисимметрично.
S антисимметрично.
8. Используя понятие мощности конечного множества, равномощности, решить задачу на доказательство. Доказать, что если А – счетное множество, В – конечное множество, то А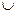 В – счетное множество.
В – счетное множество.
Вариант 11.
1. Известно, что из 90 студентов в секциях спортивного клуба занимаются: в гимнастической – 20, в волейбольной – 40, в баскетбольной – 30, в гимнастической и волейбольной – 5, в гимнастической и баскетбольной – 10, в волейбольной и баскетбольной – 7, во всех трех секциях – 2. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что  .
.
4. Даны множества  и
и  . Найти
. Найти 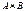 ,
, 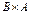 ,
,  ,
, 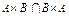 ,
, 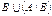 .
.
5. Доказать, что для всех 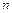 выполняется утверждение:
выполняется утверждение:
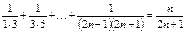 .
.
6. Пусть R – отношение на А. Доказать, что если R – рефлексивно, то R -1 тоже рефлексивно.
7. Установите, является ли заданное отношение R на N отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. 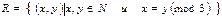 .
.
8. Упростить выражение алгебры множеств: 
Вариант 12.
2. Известно, что из 80 студентов в секциях спортивного клуба занимаются: в гимнастической – 20, в волейбольной – 40, в баскетбольной – 30, в гимнастической и волейбольной – 5, в гимнастической и баскетбольной – 10, в волейбольной и баскетбольной – 7, во всех трех секциях – 2. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество: 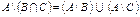 .
.
3. Доказать, что 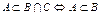 и
и 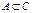 .
.
4. Даны множества  и
и  . Найти
. Найти  ,
,  ,
,  ,
,  ,
, 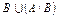 .
.
5. Доказать, что для всех 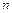 выполняется утверждение:
выполняется утверждение:
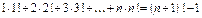 .
.
6. Пусть R – отношение на А. Доказать, что если R симметрично, то R -1 = R.
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. A = {1, 2, 3, …, 9, 10} и R = { (x, y) | x, y 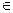 A и x + y – чётные}.
A и x + y – чётные}.
8. Упростить выражение алгебры множеств: 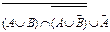 .
.
Вариант 13.
1. Известно, что из 85 студентов в секциях спортивного клуба занимаются: в гимнастической – 20, в волейбольной – 35, в баскетбольной – 30, в гимнастической и волейбольной – 5, в гимнастической и баскетбольной – 15, в волейбольной и баскетбольной – 7, во всех трех секциях – 2. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что 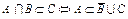 .
.
4. Даны множества 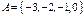 и
и  . Найти
. Найти  ,
, 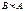 ,
, 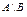 ,
,  ,
, 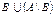 .
.
5. Доказать, что для всех 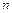 выполняется утверждение:
выполняется утверждение:
 .
.
6. Пусть задано бинарное отношение  . Какими свойствами обладает отношение R?
. Какими свойствами обладает отношение R?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. А = {1, 2, 3}, R = {(1, 1), (2, 2), (3, 3), (1, 2), (3, 2), (2, 1)}.
8. Упростить выражение алгебры множеств:  .
.
Вариант 14.
1. Известно, что из 75 студентов в секциях спортивного клуба занимаются: в гимнастической – 20, в волейбольной – 25, в баскетбольной – 30, в гимнастической и волейбольной – 7, в гимнастической и баскетбольной – 8, в волейбольной и баскетбольной – 6, во всех трех секциях – 4. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество: 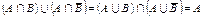 .
.
3. Доказать, что  .
.
4. Даны множества 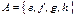 и
и  . Найти
. Найти  ,
,  ,
, 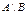 ,
, 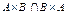 ,
, 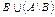 .
.
5. Доказать, что для всех 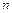 выполняется утверждение:
выполняется утверждение:
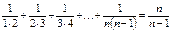 .
.
6. Заданы множество  и отношение на нём
и отношение на нём 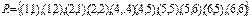 .Какими свойствами обладает отношение R?
.Какими свойствами обладает отношение R?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. А = {1, 2, 3}, R = {(1, 1), (2, 2), (3, 3)}.
8. Упростить выражение алгебры множеств:  .
.
Вариант 15.
1. Известно, что из 65 студентов в секциях спортивного клуба занимаются: в гимнастической – 17, в волейбольной – 23, в баскетбольной – 25, в гимнастической и волейбольной – 7, в гимнастической и баскетбольной – 8, в волейбольной и баскетбольной – 6, во всех трех секциях – 4. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что  .
.
4. Даны множества 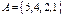 и
и 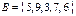 . Найти
. Найти  ,
,  ,
,  ,
,  ,
, 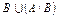 .
.
5. Доказать, что для всех 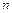 выполняется утверждение:
выполняется утверждение:
 .
.
6. Пусть заданы множество рациональных чисел Q и отношение на нём: 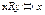 ,
, 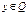 ;
; 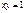 . Какими свойствами обладает указанное отношение?
. Какими свойствами обладает указанное отношение?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. А = {1, 2, 3}, R = {(2, 2), (1, 1)}.
8. Упростить выражение алгебры множеств: 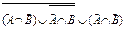 .
.
Вариант 16.
1. Известно, что из 70 студентов в секциях спортивного клуба занимаются: в гимнастической – 16, в волейбольной – 24, в баскетбольной – 30, в гимнастической и волейбольной – 5, в гимнастической и баскетбольной – 5, в волейбольной и баскетбольной – 10, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что  и
и  .
.
4. Даны множества  и
и 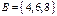 . Найти
. Найти  ,
, 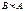 ,
, 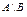 ,
,  ,
,  .
.
5. Доказать, что для всех 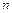 выполняется утверждение:
выполняется утверждение:
 .
.
6. Пусть А – множество прямых на плоскости и задано отношение R: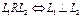 . Какими свойствами обладает данное отношение?
. Какими свойствами обладает данное отношение?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. Множество А = {-10, -9, -8, -7, …, 0, 1, …9, 10} и (a, b) 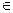 R, если a 3 = b 3.
R, если a 3 = b 3.
8. Упростить выражение алгебры множеств:  .
.
Вариант 17.
1. Известно, что из 60 студентов в секциях спортивного клуба занимаются: в гимнастической – 15, в волейбольной – 20, в баскетбольной – 25, в гимнастической и волейбольной – 5, в гимнастической и баскетбольной – 5, в волейбольной и баскетбольной – 10, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что  .
.
4. Даны множества 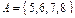 и
и  . Найти
. Найти  ,
, 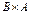 ,
, 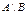 ,
, 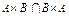 ,
, 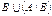 .
.
5. Доказать, что для всех натуральных 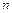 выполняется утверждение:
выполняется утверждение:
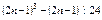 .
.
6. На множестве действительных чисел задано отношение  . Какими свойствами оно обладает?
. Какими свойствами оно обладает?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. Множество А = {-10, -9, -8, -7, ..., 0, 1, …9, 10} и (a, b) 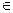 R, если a 2 = b 2.
R, если a 2 = b 2.
8. Упростить выражение алгебры множеств: 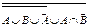 .
.
Вариант 18.
1. Известно, что из 95 студентов в секциях спортивного клуба занимаются: в гимнастической – 25, в волейбольной – 40, в баскетбольной – 30, в гимнастической и волейбольной – 10, в гимнастической и баскетбольной – 8, в волейбольной и баскетбольной – 5, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что 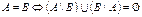 .
.
4. Даны множества  и
и 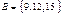 . Найти
. Найти 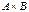 ,
, 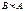 ,
, 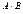 ,
, 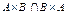 ,
, 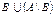 .
.
5. Доказать, что для всех 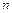 выполняется утверждение:
выполняется утверждение:
 .
.
6. На множестве 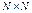 задано отношение
задано отношение  . Какими свойствами обладает данное отношение?
. Какими свойствами обладает данное отношение?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. А – множество упорядоченных пар целых чисел, и (a, b) R (c, d), если ad = bc.
8. Упростить выражение алгебры множеств:  .
.
Вариант 19.
1. Известно, что из 100 студентов в секциях спортивного клуба занимаются: в гимнастической – 28, в волейбольной – 30, в баскетбольной – 42, в гимнастической и волейбольной – 8, в гимнастической и баскетбольной – 10, в волейбольной и баскетбольной – 5, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество: 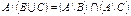 .
.
3. Доказать, что 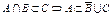 .
.
4. Даны множества  и
и 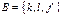 . Найти
. Найти  ,
, 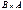 ,
,  ,
,  ,
, 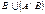 .
.
5. Доказать, что для всех 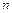 выполняется утверждение:
выполняется утверждение:
 .
.
6. Заданы два отношения R1 и R2, R1 – симметричное, рефлексивное, R2 – антисимметричное, антирефлексивное. Какими свойствами обладает отношение  ?
?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. {( x, y) | x, y 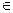 A = Z и x + y = 5}.
A = Z и x + y = 5}.
8. Упростить выражение алгебры множеств:  .
.
Вариант 20.
1. Известно, что из 75 студентов в секциях спортивного клуба занимаются: в гимнастической – 20, в волейбольной – 25, в баскетбольной – 30, в гимнастической и волейбольной – 7, в гимнастической и баскетбольной – 8, в волейбольной и баскетбольной – 6, во всех трех секциях – 4. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?
2. Доказать тождество:  .
.
3. Доказать, что  .
.
4. Даны множества  и
и  . Найти
. Найти  ,
, 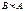 ,
,  ,
,  ,
, 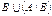 .
.
5. Доказать, что для всех натуральных 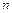 выполняется утверждение:
выполняется утверждение:
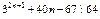 .
.
6. Заданы два отношения R1 и R2, R1 – рефлексивное, транзитивное, R2 – антирефлексивное, транзитивное. Какими свойствами обладает отношение 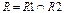 ?
?
7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. {( x, y) | x, y 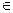 A = Z и x + y = 0}.
A = Z и x + y = 0}.
8. Упростить выражение алгебры множеств:  .
.