Линейная зависимость и независимость векторов линейного пространства.
Дана система векторов а1, а2, а3, … аn Є линейному пространству L.
Опр. Вектор α1 а1+ α2 а2+…+ αn аn Є L, где αi (i = 1,…,n)- числа, называется линейная комбинация векторов а1, а2, а3, … аn.
Опр. Система векторов линейного пространства а1, а2, а3, … аn Є L называется линейно независимой (ЛНЗ), если линейная комбинация α1 а1+ α2 а2+α3 а3+…+ αn аn=0 тогда и только тогда, когда коэффициенты α 1 =α 2 =α 3 =α n=0.
Опр. Система векторов а1, а2, а3, … аn Є L называется линейно зависимой (ЛЗ), если существует набор чисел α1, α2 ,α3 … αn не все из которых равны 0, такие что линейная комбинация α1 а1+ α2 а2+…+ αn аn= 0.
Пр. 1) Два вектора называются коллинеарными, если они параллельны одной прямой.
2) Рассмотрим два ненулевых, неколлинеарных вектора на плоскости. Диагональ 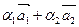 =0
=0 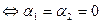

а1 α1 а1
Вывод: Два не нулевых, не коллинеарных вектора на плоскости линейно независимы.
3 ) а1 ║а2
) а1 ║а2
|


|
Вывод: Линейная комбинация равна нулю, есть не нулевой коэффициент, следовательно, два коллинеарных вектора на плоскости линейно зависимы.