Системы линейных уравнений.

Конечную совокупность линейных уравнений относительно неизвестных х1, х2, …, хn называют системой линейных уравнений. Если перенумеровать уравнения системы, то система линейных уравнений запишется в следующем общем виде:

 

а11 х1 + а12 х2 +…+ а1n хn= b1,

а21 х1 + а22х2 +…+ а2 n хn= b2, (1)

………………………….

а m1 х1 + а m2 х2 +…+ а m n хn= b m,

где аij –коэффициент при неизвестном хj из i – того уравнения, bi – свободный член i – того уравнения системы.

Числа а11 , а12 , …, а mn называют коэффициентами, а b1,b2, … , b m – свободными членами системы линейных уравнений.

Системы линейных уравнений часто записывают в виде таблицы:

 

х1 х2 … хn

а11 а12 а1n b1,

а21 а22 а2 n b2,

…………………….

а m1 а m2 а m n b m,

 

Решением системы уравнений называют такой упорядоченный набор чисел

k1, k2, …, kn , который является решением каждого уравнения системы. Решить систему уравнений - значит найти все её решения или убедиться, что в том, что их нет.

Система уравнений либо несовместна (не имеет ни одного решения ), либо является определённой ( имеет единственное решение ), либо является неопределённой ( имеет бесконечное множество решений ).

Систему уравнений, которая имеет хотя бы одно решение, называют совместной.

Если одно из уравнений системы является противоречивым, то система несовместна.

Две системы линейных уравнений называют равносильными, если они имеют одни и те же решения.

 

 

Метод Гаусса построения решения системы линейных уравнений.

Среди многочисленных методов решения систем линейных уравнений одним из наиболее удобных как для практических целей, так и для теоретических выводов является метод последовательного исключения неизвестных, или метод Гаусса.

Сущность метода Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к виду, из которого все её решения усматриваются непосредственно.

Решение строят из исходной системы уравнений с помощью элементарных преобразований, под которыми понимается любое из следующих действий:

1) вычёркивание уравнения, у которого все коэффициенты при неизвестных и свободный член равны 0, т.е. уравнения вида

2) умножение обеих частей какого-либо уравнения системы на отличное от нуля число;

3) замена i–того уравнения системы уравнением, которое получается путём прибавления к i–тому уравнению системы её j–того уравнения, умноженного на число;

4) перестановка во всех уравнениях членов с какими-нибудь двумя неизвестными.

Элементарные преобразования переводят данную систему уравнений в равносильную ей систему.

Возможны два случая.

Случай 1. Среди уравнений системы имеется уравнение следующего вида

(2)

где b –число, не равное 0. Никакой набор значений неизвестных такому уравнению удовлетворять не может, поэтому система, содержащая такое уравнение, несовместна.

Случай 2. В системе нет уравнений такого вида. Иначе говоря, в каждом уравнении системы хотя бы один из коэффициентов при неизвестных отличен от 0. Остановимся на этом случае. Предположим, что а11 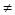0. Тогда можно из всех уравнений систем начиная со второго исключить неизвестное х1 . Для этого ко второму уравнению прибавляем первое, умноженное на -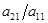. К третьему уравнению – первое, умноженное

на - 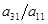, и т.д.. В результате система принимает вид

…………

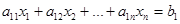
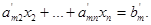
Первый шаг закончен. С помощью рамки отделена часть системы, подлежащая дальнейшим преобразованиям, - остаточная часть.

Повторим теперь предыдущие рассуждения, но уже применительно к остаточной части системы. В результате или обнаружим уравнение

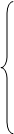вида (2), и тем самым установим, что система несовместна, или же, предположив, что 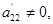сделаем следующий шаг – перейдём к системе вида

…………

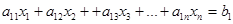
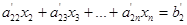
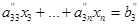
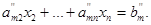
На этом заканчивается второй шаг. Новая остаточная часть системы содержит на одно уравнение меньше.

Продолжая этот процесс, приходим к одному из двух случаев. Либо после какого-то шага получится система, остаточная часть которой содержит уравнение вида (2). Тогда исходная система несовместна и преобразовывать её дальше не имеет смысла.

Либо, поскольку число шагов не может превысить n (числа неизвестных), мы рано или поздно придём к системе без остаточной части, т.е.

…………

 

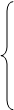
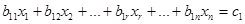
где диагональные коэффициенты b11, b22, …,brr отличны от 0. Возможное изменение числа уравнений по сравнению с исходной системой(r вместо m)

связано с тем, что в процессе преобразований отбрасывают уравнения

вида (2). Такая система называется лестничной..Коэффициент при неизвестном в первом члене первого уравнения системы называется ключевым.

 

Пример 1. Решить систему

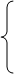2х1 – х2 + х3 – х4 = 2

2х1 – х2 – 3х4 = 1

3х1 - х3 + х4 = 8

2х1 + 2х2 - 2х3 + 5х4 = 11

Здесь ключевой коэффициент не равен 0, однако всё же удобно начать с перестановки (в каждом уравнении) членов с х1 и х2. Получаем систему

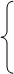– х2 + 2х1 + х3 – х4 = 2

– х2 + 2х1 – 3х4 = 1

3х1- х3 + х4 = 8

2х2+ 2х1 - 2х3 + 5х4 = 11

Далее имеем

 

– х2 + 2х1 + х3 – х4 = 2

0х1 – х3 - 2х4 = -1

3х1 - х3 + х4 = 8

6х1 - 0х3 + 3х4 = 15

 

– х2 + 2х1 + х3 – х4 = 2

– х3 + 0х1 - 2х4 = -1

- х3 + 3х1 + х4 = 8

0х3 + 6х1 + 3х4 = 15

 

– х2 + 2х1 + х3 – х4 = 2

– х3 + 0х1 - 2х4 = -1

3х1 + 3х4 = 9

6х1 + 3х4 = 15

– х2 + 2х1 + х3 – х4 = 2

– х3 + 0х1 - 2х4 = -1

3х1 + 3х4 = 9

-3х4 = -3

Последняя система имеет треугольный вид; движением снизу вверх находим единственное решение: х4 =1, х1 = 2, х2 = 0, х3= -1.

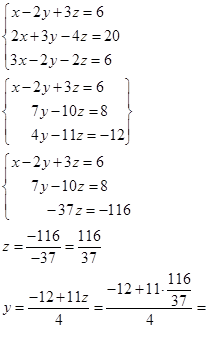
Пример2.

-х1 + 3х2 + 3х3 + 2х4 + 5х5 = 2

-3х1 + 5х2 + 2х3 + 3х4 + 4х5 = 2

-3х1 + х2 – 5х3 -7х5 = -2

-5х1 + 7х2 + х3 + 16х4 + х5 = 10

Ключевой коэффициент в системе отличен от 0 (равен –1). Используя это, исключаем х1 из всех уравнений начиная со второго. Для этого из второго, третьего и четвёртого уравнений вычитаем первое, умноженное соответственно на –3, -3, -5. Получаем систему

 

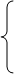-х1 + 3х2 + 3х3 + 2х4 + 5х5 = 2

-4х2 - 7х3 - 3х4 - 11х5 = -4

-8х2 - 14х3 - 6х4 - 22х5 = -8

-8х2 - 14х3 + 6х4 - 24х5 = 0

В остаточной части этой системы ключевой коэффициент отличен

от 0 (равен –4). Используя это, исключаем х2 из всех уравнений остаточной системы начиная со второго. В результате получаем систему

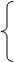-х1 + 3х2 + 3х3 + 2х4 + 5х5 = 2

-4х2 - 7х3 - 3х4 - 11х5 = -4

0х3 + 12х4 - 2х5 = 8

( уравнений стало на одно меньше, т.к. отброшено уравнение 0=0). В остаточной части ключевой коэффициент (при х3) равен 0, но зато отличен от 0 коэффициент, например, при х5. Переставляя в каждом уравнении члены с х3 и х5, получаем систему

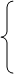-х1 + 3х2 + 5х5 + 2х4 + 3х3 = 2

-4х2 -11х5 - 3х4 - 7х3 = -4

- 2х5 + 12х4 = 8

Система содержит пять неизвестных и три уравнения, следовательно, она имеет бесконечное множество решений.

Полагаем неизвестные х3 и х4 свободными:

 

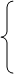-х1 + 3х2 + 5х5 = - 2х4 - 3х3 +2

-4х2 -11х5 = 3х4 + 7х3 -4

- 2х5 = - 12х4 + 8.

Придадим им произвольные значения, например х3 = 1, х4 =1, тогда

х5 = 2, х2 =-7, х1 =-8. Итак (-8, -7, 1, 1, 2) – частное решение системы. Неизвестные х5, х2, х1 называются базисными.

 

 

Процесс решения системы методом Гаусса можно упростить. Если, вместо того чтобы преобразовывать систему преобразовывать соответствующую матрицу. Элементарным преобразованиям, выполняемым над системой, отвечают преобразования над её матрицей:

перестановке неизвестных соответствует перестановка двух столбцов;

вычёркиванию уравнения соответствует вычёркивание строки, состоящей из одних нулей,

прибавлению к одному из уравнений системы другого, умноженного на некоторое число, соответствует прибавление к одной из строк матрицы другой строки, умноженной на число.

Эти преобразования над матрицей системы будем также называть элементарными.

 

Проиллюстрируем это на примере системы из примера 1. Выпишем матрицу системы:

х1 х2 х3 х4 х2 х1 х3 х4

~ ~

 

 

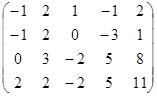х2 х1 х3 х4 х2 х3 х1 х4

~ ~ ~

 

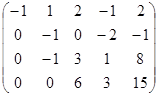х2 х3 х1 х4 х2 х3 х1 х4

~ ~ .

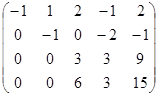Знак ~ означает, что проводится элементарное преобразование системы.,

Пример 3. Решить систему

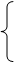2х1 – х2 +3х3 – 2х4 + 4х5 = -1

4х1 – 2х2 +5х3 + х4 + 7х5 = 2

2х1 – х2 +х3 + 8х4 + 2х5 = 1 .

Имеем

х1 х2 х3 х4 х5 х1 х2 х3 х4 х5

~ ~

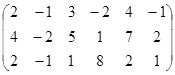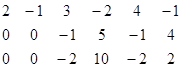х1 х3 х2 х4 х5 х1 х3 х2 х4 х5

~ ~ .

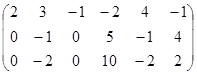Последней строке отвечает уравнение

0х1 +0х2 +0х3 + 0х4 + 0х5 = -6, показывающее, что система не имеет решений ( несовместна ).