Система линейных алгебраических уравнений .Метод Крамера уравнений
Совокупность уравнений :

относительна неизвестных x1, x2, ..., xn-1, xn называется системой линейных алгебраических уравнений.
Числа aij — коэффициенты системы, bi— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.
Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.
Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.
Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.
Если среди правых частей bi системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.
Если все правые части системы равны нулю, то система называется однородной.
Система линейных уравнений может быть записана в матричной форме A·x = b:
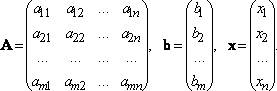
Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
A(1)x1 + A(2)x2 + ... + A(n)xn = b.
Здесь A(1), A(2), ... , A(n) — столбцы матрицы системы.

Матрица Ap называется расширенной матрицей системы.
Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.
МЕТОД КРАМЕРА!
Пусть дана система линейных уравнений

Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn
ý - называется решением системы (1), если при подстановке этих чисел
вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij
ç, составленный из коэффициентов при неизвестных , называется
определителем системы (1). В зависимости от определителя системы (1) различают
следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может
быть найдено по формулам Крамера : x1=
, где
определитель n-го порядка Di ( i=1,2,...,n) получается из
определителя системы путем замены i-го столбца свободными членами b1
, b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо
несовместна ,т.е. решений нет.