Теорема о соответствии угловой точки опорного плана ( Теорема №4).

 

Основные теоремы линейного программирования

Для обоснования методов решения задач линейного программирования сформулируем ряд важнейших теорем, опуская их аналитические доказательства. Уяснить смысл каждой из теорем поможет понятие о геометрической интерпретации решения ЗЛП, данное в предыдущем подразделе.

Однако сначала напомним о некоторых понятиях, важных с точки зрения дальнейшего разговора.

Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными).

Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

В частном случае, когда в систему ограничений входят только две переменные x1 и x2, это множество можно изобразить на плоскости. Так как речь идет о допустимых решениях (x1, x2 ≥ 0), то соответствующее множество будет располагаться в первой четверти декартовой системы координат. Это множество может быть замкнутым (многоугольник), незамкнутым (неограниченная многогранная область), состоять из единственной точки и, наконец, система ограничений-неравенств может быть противоречивой.

Теорема 2. Если задача линейного программирования имеет оптимальное решение, то оно совпадает с одной (двумя) из угловых точек множества допустимых решений.

Из теоремы 2 можно сделать вывод о том, что единственность оптимального решения может нарушаться, причем, если решение не единственное, то таких оптимальных решений будет бесчисленное множество (все точки отрезка, соединяющего соответствующие угловые точки).

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений, и наоборот.

Следствием из теорем 2 и 3 является утверждение о том, что оптимальное решение (оптимальные решения) задачи линейного программирования, заданной (или приведенной) ограничениями-уравнениями, совпадает с допустимым базисным решением (допустимыми базисными решениями) системы ограничений.

Таким образом, оптимальное решение ЗЛП следует искать среди конечного числа допустимых базисных решений.

57. Симплекс-метод, два этапа метода:

— Нахождение исходного опорного плана , канонический вид ЗЛП

— Симплекс-алгоритм.

Симплекс-метод – один из наиболее эффективных методов численного решения задач ЛП. Суть понятия «симплекс» заключается в следующем. Для тела в k -мерном пространстве симплексом называется множество, состоящее из k +1 вершин этого тела. Так, при k = 2, т.е. на плоскости, симплексом будут вершины треугольника; при k = 3 симплексом являются вершины четырехгранника, например тетраэдра, и т.д. Такое название методу дано по той причине, что в его основе лежит последовательный перебор вершин ОДЗП с целью определения координат той вершины, в которой функция цели имеет кстремальное значение.

Решение задачи с помощью симплекс-метода разбивается на два основных этапа. На первом этапенаходят одно из решений, удовлетворяющее системе ограничений . Системы, в которых переменных больше, чем ограничений N > m, называются неопределенными. Они приводятся к определенным системам (N = m) путем приравнивания к нулю N-m каких-либо переменных. При этом остается система m уравнений с m неизвестными, которая имеет решение, если определитель системы отличен от нуля. В симплекс-методе вводится понятие базисных переменных, или базиса. Базисом называется любой набор из m таких переменных, что определитель, составленный из коэффициентов при этих переменных в m-ограничениях, отличен от нуля. Остальные N-m переменных называются небазисными, или свободными переменными. Если принять, что все небазисные переменные равны нулю, и решать систему ограничений относительно базисных переменных, то получим базисное решение.

В системе из m уравнений с N неизвестными общее число базисных решений при N > m определяется числом сочетаний

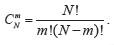
Базисное решение, в котором все xi0, i = 1,m, называется допустимым базисным решением. Таким образом, первый этап решения, используя симплекс-метод, завершается нахождением допустимого базисного решения, хотя бы и неудачного.

На втором этапе производится последовательное улучшение найденного решения. При этом осуществляется переход от одного допустимого базисного решения к другому таким образом, чтобы значение целевой функции улучшилось. Процесс решения, используя симплекс-метод, продолжается до тех пор, пока не будет достигнуто наименьшее (или наибольшее) значение функции цели. Геометрически это означает переход по ребрам из одной вершины многогранника допустимых значений в другую по направлению к той, в которой значение функции цели достигает экстремума. Симплекс-метод дает оптимальную процедуру перебора базисных решений и обеспечивает сходимость к экстремальной точке за конечное число шагов. Используя симплекс-метод, вычисления на втором этапе ведутся по следующей схеме:

1) базисные переменные и функция цели выражаются через небазисные переменные;

2) по определенному правилу выбирается та из небазисных переменных, изменение значения которой способно улучшить значение F(x) , и она вводитя в базис;

3) определяется, какая из базисных переменных должна быть выведена из базиса, при этом новый набор базисных переменных, образующийся на каждом шаге, отличается от предыдущего только одной переменной;

4) базисные переменные и функция цели выражаются через новые небазисные переменные, и повторяются операции 2) и 3).

Если на определенном шаге в симплекс-методе окажется, что изменение значений любой из небазисных переменных не может улучшить F(x) , то последнее базисное решение оказывается оптимальным.

Рассмотрим пример, относящийся к задачам организационно-экономического управления и помогающий уяснить содержание симплекс-метода.

Пример 1. На приобретение оборудования для нового участка выделено 20 тыс. y.e. Оборудование должно быть размещено на площади, не превышающей 72 м^2. Может быть заказано оборудование двух видов: 1) оборудование стоимостью 5 тыс. y.e., занимающее площадь 6 м^2 и дающее 8 тыс. ед. продукции за смену; 2) оборудование стоимостью 2 тыс. y.e., занимающее площадь 12 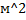и дающее за смену 4 тыс. ед. продукции. Найти оптимальный вариант приобретения оборудования, обеспечивающий максимум общей производительности участка, используя симплекс-метод.

Обозначим неизвестное количество оборудования первого и второго видов соответственно через x1 и x2. Функция цели может быть записана следующим образом: F(x) = 8x1 + 4x2(max). Ограничения по площади: 6x1 +12x2≤72; ограничения по стоимости: 5x1 + 2x2≤20 ; ограничения на знак переменных x1≥0 ; x2≥0.

Разделим коэффициенты первого из ограничений на 6 и приведем ограничения к виду равенств, вводя дополнительные переменные x3 и x4:

x1 + 2x2 + x3 =12, (1)

5x1 + 2x2 + x4 = 20 . (2)

Таким образом, ограничения задачи при решение симплекс-методом, приведены к системе из двух алгебраических уравнений с четырьмя неизвестными. Процедура решения задачи следующая:

1-й шаг. Для решения симплекс-методом выберем в качестве базисных переменных (БП) x2 и x4, так как определитель, составленный из коэффициентов при этих переменных в ограничениях задачи отличен от нуля.

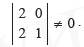
Тогда x1 и x3 будут небазисными переменными (НП). Выразим базисные переменные и F(x) через небазисные.

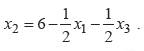(3)

Из второго ограничения следует, что

x4 = 20 - 2x2 - 5x1. (4)

С учетом выше приведенного выражения получим

x4 = 8 - 4x1 + x3. (5)

Тогда

F(x) = 8x1 + 4x2 = 24 + 6x1 - 2x3 . (6)

На каждом шаге решения задачи симплекс-методом НП приравниваются к нулю, следовательно, БП и F(x) будут равны свободным членам в соответствующих выражениях:

x1 = 0, x3 = 0, x2 = 6, x4 = 8, F(x) = 24.

Это решение соответствует координатам вершины A ОДЗП на рис. 1. Оптимальность решения проверяется по выражению F(x) для функции цели. Переменная x3 входит в это выражение с отрицательным коэффициентом; если вводить x3 в базис на следующем шаге, то она примет положительное значение, и от числа 24 некоторая величина будет вычитаться, т.е. значение F(x) уменьшится. Если же вводить в базис на следующем шаге x1, то значение функции цели увеличится, т.е. улучшится.

Применяя симплекс-метод, из базиса исключают ту переменную, которая раньше обратится в нуль при введении в базис x1. Анализируя (3) и (5), определяем, что из базиса следует исключить x4. На следующем шаге местами поменяются переменные x1 и x4.

2-й шагсимплекс-метода. x1 и x2 – базисные переменные, x3 и x4 – небазисные. Выразим базисные переменные и F(x) через небазисные переменные. Из (5) следует

x1=2+(1/4)x3-(1/4)x4 (7)

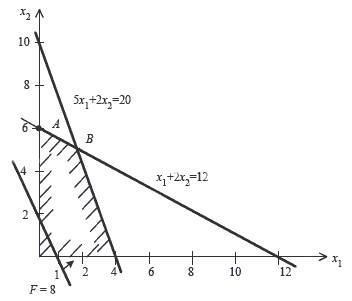
Рис. 1. Графическая интерпритация к примеру 1, используя симплекс-метод.

Подставив (7) в (3), получим

x2=5-(5/8)x3+(1/8)x4

Тогда F(x) = 8x1 + 4x2 = 36 - (1/2)x3 -(3/4)x4 . В результате x3 = x4 = 0 (как небазисные), x1 = 2, x2 = 5, F = 36 . Это решение соответствует координатам вершины В на рис. 1. Найденное решение симплекс-методом будет оптимальным, улучшить значение F(x) нельзя, так как переменные x3 и x4 входят в выражение для функции цели с отрицательными коэффициентами.

Таким образом, применяя симплекс-метод, нашли, что максимальная производительность участка 36 тыс. ед. продукции за смену будет обеспечена при закупке 2 ед. оборудования первого вида и 5 ед. оборудования второго вида. Дополнительные переменные x3 и x4 имеют смысл неиспользованных ресурсов. В данном примере все ресурсы по площади и по стоимости использованы полностью (x3 = x4 = 0).